Luvut ja yhtälöt (MAY1)
Laajuus
2 op
Yleiset tavoitteet (LOPS 2021)
Moduulin tavoitteena on, että opiskelija
- kertaa prosenttilaskennan periaatteet
- osaa käyttää verrannollisuutta ongelmanratkaisussa
- syventää murtolukujen laskutoimitusten osaamistaan
- kertaa potenssin laskusäännöt
- vahvistaa ymmärrystään funktion käsitteestä
- ymmärtää yhtälön ja yhtälöparin ratkaisemisen periaatteet
- oppii käyttämään ohjelmistoja funktion kuvaajan piirtämisessä, havainnoinnissa ja yhtälöiden ratkaisemisessa.
Keskeiset sisällöt (LOPS 2021)
- lukujoukot ja peruslaskutoimitukset
- luvun vastaluku, käänteisluku ja itseisarvo
- prosenttilaskenta
- potenssin laskusäännöt (eksponenttina kokonaisluku)
- suoraan ja kääntäen verrannollisuus
- funktio, kuvaajan piirto ja kuvaajan tulkinta
- ensimmäisen asteen yhtälön ratkaiseminen
- yhtälöpari
- neliö- ja kuutiojuuri
- potenssifunktio ja potenssiyhtälö (asteluvut 2 ja 3)
Aikataulu
Suoritus
- riittävä läsnäolo
- lähtötasotesti
- tehtävien tekeminen
- viikkotehtävät (4 kpl)
- loppukoe
Arviointi
- viikkotehtävät (3 parasta), painoarvo päättöarvosanasta 25 %
- loppukoe, painoarvo päättöarvosanasta 75 %
- viikkotehtävissä ja loppukokeessa 30 % arviointi
Keskeyttäminen
Opettaja keskeyttää opiskelijan opintojakson, jos
- opiskelija niin pyytää
- opiskelija ei ole läsnä opintojakson kahdella ensimmäisellä opetuskerralla ja opiskelija ei ole yhteydessä opettajaan eikä opettaja saa yhteyttä opiskelijaan.
Opettaja voi keskeyttää opiskelijan opintojakson, jos opiskelijalla on neljä poissaoloa. Tällaiset tilanteet opettaja käy läpi tapauskohtaisesti ja on ennen lopullista keskeytystä yhteydessä opiskelijaan.
Keskeyttämisestä opettaja merkitsee opintojaksosta opiskelijalle K-merkinnän Wilmaan ja poistaa opiskelijan sen jälkeen Wilman ryhmästä. Opettaja lähettää keskeyttämisestä viestin opiskelijalle, alaikäisen opiskelijan huoltajalle, ryhmänohjaajalle ja opolle.
1 LUVUT JA LASKUTOIMITUKSET
1.1 Lukujoukot
Luonnolliset luvut
$$ \mathbb{N}=\{0, 1, 2, 3, ... \} $$
Luonnollisilla luvuilla voidaan ilmoittaa lukumääriä.
Kun luonnollisten lukujen joukkoa laajennetaan positiivisten kokonaislukujen vastaluvuilla eli negatiivisilla kokonaisluvuilla, saadaan kokonaislukujen joukko.
Kokonaisluvut
$$\mathbb{Z}=\{... , -3, -2, -1, 0, 1, 2, 3, ... \}$$
Kokonaislukuja kuvaavat lukusuoralla tasavälein (yhden yksikön välein) esiintyvät viivat.
Lukusuoran yhden yksikön mittaiset välit voidaan jakaa tasaosiin eri tavoin. Näin syntyvien lukujen joukkoa kutsutaan rationaaliluvuiksi.
Rationaaliluvut
$$\mathbb{Q}=\left\{\frac{m}{n} \mid m, n\in\mathbb{Z},\ n\neq0\right\}$$
Rationaalilukuja ovat luvut, jotka voidaan esittää murtolukumuodossa. Desimaalimuodossa tällaiset luvut ovat päättyviä tai päättymättömiä, jaksollisia desimaalilukuja.
Esim. 1
\(-5=-\frac{5}{1}\); \(3{,}2=3\frac{1}{5}=\frac{16}{5}\) ja \(0{,}333\ldots=\frac{1}{3}\) ovat rationaalilukuja.
Lukuja, joita ei voida esittää murtolukumuodossa, kutsutaan irrationaaliluvuiksi.
Reaaliluvut
Reaalilukujen joukon \(\mathbb{R}\) muodostavat rationaali- ja irrationaaliluvut yhdessä.
Irrationaaliluvut ovat desimaalimuodossa päättymättömiä ja jaksottomia eli desimaaliosassa ei toistu jokin sama numerosarja säännöllisesti.
Esim. 2
\(\sqrt{2}\approx1{,}41\) ja \(\pi\approx3{,}14\) ovat irrationaalilukuja.
1.2 Lukusuora
Lukusuoran jatkuva viiva kuvaa kaikkia mahdollisia reaalilukuja. Lukusuora on samalla lukujen suuruusjärjestys.

Luvun itseisarvo kuvaa luvun etäisyyttä nollasta lukusuoralla. Luvun \(a\) itseisarvo merkitään \(|a|=a\) ja luvun \(-a\) itseisarvo \(|-a|=a\).
Luvun itseisarvo on aina positiivinen luku (etäisyys ei voi olla negatiivinen).
Vastaluvut sijaitsevat lukusuoralla nollan vastakkaisilla puolilla yhtä kaukana nollasta. Vastaluvuilla on siis sama itseisarvo.
Luvun \(a\) vastaluku merkitään \(-a\). Luvun \(-a\) vastalukua voidaan merkitä \(-(-a)=a\).
1.3 Reaalilukujen laskulait
Reaaliluvuilla pätevät seuraavat laskulait. Näitä lakeja kutsutaan aksioomiksi. Matematiikassa aksiooma tarkoittaa perustavanlaatuista lainalaisuutta, jota ei voida perustella muilla säännöillä tai johtaa muista säännöistä.
Reaalilukujen laskulait (kunta-aksioomat)
Olkoot \(a\), \(b\) ja \(c\) reaalilukuja.
(1) Yhteenlaskun vaihdantalaki $$a+b=b+a.$$
(2) Kertolaskun vaihdantalaki $$ab=ba.$$
(3) Yhteenlaskun liitäntälaki $$a+(b+c)=(a+b)+c.$$
(4) Kertolaskun liitäntälaki $$a(bc)=(ab)c.$$
(5) Osittelulaki $$a(b+c)=ab+ac.$$
(6) Nolla
Nolla on luku, jolle pätee \(a+0=a\). Toisin sanoen nollan lisääminen ei muuta lukua.
(7) Ykkönen
Ykkönen on luku, jolle pätee \(1\cdot a=a\). Toisin sanoen ykkösellä kertominen ei muuta lukua.
(8) Vastaluku
Luvulla \(a\) on vastaluku \(-a\). Vastalukujen summa on 0: $$a+(-a)=a-a=0.$$
(9) Käänteisluku
Luvulla \(a\) on käänteisluku \(\frac{1}{a}\). Käänteislukujen tulo on 1: $$a\cdot\frac{1}{a}=1.$$
Voidaan myös sanoa, että luvut joiden tulo on 1, ovat toistensa käänteislukuja.
1.4 Luvuilla laskeminen
Merkkisääntö
$$++\quad\rightarrow \quad+$$ $$--\quad\rightarrow \quad+$$
$$+-\quad\rightarrow \quad-$$
$$-+\quad\rightarrow \quad-$$Esim. 1
a) \(-4+(-6)=-4-6=-10\)
b) \(5-(-3)=5+3=8\)
Yhteen- ja vähennyslaskussa sulkeet poistetaan ja kahdesta peräkkäisestä laskutoimitusmerkistä päätellään merkkisäännön mukaisesti voimaan jäävä merkki.
Esim. 2
a) \(5\cdot(-3)=-15\)
b) \(-4\cdot(-6)=24\)
Kertolaskussa, jos tulontekijät ovat samanmerkkiset, tulo on positiivinen, ja jos tulontekijät ovat erimerkkiset, tulo on negatiivinen. Jakolaskussa osamäärän merkki päätellään vastaavasti jaettavan ja jakajan etumerkeistä.
Yhdistettyjä laskutoimituksia
Jotta tietäisimme, missä järjestyksessä useita laskutoimituksia sisältävät laskut tulee suorittaa, on sovittu laskujärjestyksestä.
Laskujärjestyssopimus
- Sulkeet
- Potenssit ja neliöjuuret
- Kerto- ja jakolaskut
- Yhteen- ja vähennyslaskut
Esim. 1
\(4+(5-2)^2\cdot7\)
\(=4+3^2\cdot7\)
\(=4+9\cdot7\)
\(=4+63\)
\(=67\)
Esim. 2
\(\sqrt{9+16}\)
\(=\sqrt{25}\)
\(=5\)
Juurimerkin alla olevat laskutoimitukset suoritetaan ennen juuren ottamista.
Esim. 3
\(\displaystyle{\frac{4\cdot(-5)}{-9+7}}\)
\(=\displaystyle{\frac{-20}{-2}}\)
\(=10\)
Jakoviivan ylä- ja alapuolella olevat laskutoimitukset suoritetaan ennen jakoviivalla merkityn jakolaskun laskemista.
Huom.
Aksioomat ovat matemaattisesti vahvempia sääntöjä kuin laskujärjestyssopimus. Joissain tilanteissa voidaankin laskujärjestyksestä poiketa ja käyttää aksioomia tehtävän ratkaisemiseen.
Esim. 4
\(4\cdot(250+0{,}25)\)
\(=4\cdot250+4\cdot0{,}25\)
\(=1000+1\)
\(=1001\)
Itseisarvoilla laskeminen
Itseisarvoilla laskettaessa itseisarvomerkkien sisällä olevat laskutoimitukset lasketaan ennen itseisarvon ottamista ja itseisarvomerkkien ulkopuolella olevat laskutoimitukset lasketaan vasta itseisarvon ottamisen jälkeen.
Esim. 1
\(|3-1|+|1-3|\)
\(=|2|+|-2|\)
\(=2+2\)
\(=4\)
1.5 Murtoluvut
Samannimisten murtolukujen yhteen- ja vähennyslasku
Esim. 1
$$\frac{2}{7}+\frac{3}{7}=\frac{2+3}{7}=\frac{5}{7}$$
Samannimisten murtolukujen yhteen- ja vähennyslaskussa osoittajat yhdistetään.
Esim. 2
$$\frac{5}{8}-\frac{1}{8}=\frac{4}{8}^{(4} =\frac{1}{2}$$
Vastaukset supistetaan yksinkertaisimpaan muotoon. Supistamisessa osoittaja ja nimittäjä jaetaan samalla luvulla.
Esim. 3
$$\frac{3}{4}+\frac{3}{4}=\frac{6}{4}^{(2}=\frac{3}{2}=1\frac{1}{2}$$
Jos osoittaja on suurempi kuin nimittäjä, voidaan vastaus muuttaa sekaluvuksi.
Esim. 4
$$4\frac{2}{5}+2\frac{1}{5}=6\frac{3}{5}$$
Sekalukuja, joiden murto-osat ovat samannimisiä, voidaan laskea yhteen ja vähentään yhdistämällä kokonaisosat ja murto-osat erikseen. Tämä on helpoin tapa, kun laskussa ei tapahdu kokonaisten ylitystä.
Esim. 5
$$2\frac{1}{3}-1\frac{2}{3}=\frac{7}{3}-\frac{5}{3}=\frac{2}{3}$$
\(2\frac{1}{3}=\frac{2\ \cdot\ 3\ +\ 1}{3}=\frac{7}{3}\) ja
\(1\frac{2}{3}=\frac{1\ \cdot\ 3\ +\ 2}{3}=\frac{5}{3}\)
Jos tapahtuu kokonaisten ylitys, etenkin vähennyslaskuissa on helpointa muuttaa sekaluvut murtoluvuiksi ennen laskemista.
Erinimisten murtolukujen yhteen- ja vähennyslasku
Esim. 1
$${ ^{2)}\atop }\frac{3}{5}+\frac{1}{10}=\frac{6}{10}+\frac{1}{10}=\frac{7}{10}$$
Erinimiset murtoluvut on lavennettava (tai joskus supistettava) samannimisiksi ennen yhteen- ja vähennyslaskua.
Esim. 2
$${ ^{3)}\atop }\frac{1}{2}-{ ^{2)}\atop }\frac{1}{3}=\frac{3}{6}-\frac{2}{6}=\frac{1}{6}$$
Usein laventaminen samannimisiksi onnistuu ristiin laventamalla eli laventamalla toista murtolukua ensimmäisen nimittäjällä ja ensimmäistä toisen nimittäjällä.
Esim. 3
$${ ^{5)}\atop }-\frac{1}{4}+{ ^{4)}\atop }\frac{1}{5}=-\frac{5}{20}+\frac{4}{20}=\frac{-5+4}{20}=-\frac{1}{20}$$
Negatiivisilla murtoluvuilla yhteen- ja vähennyslaskuja laskettaessa etumerkit huomioidaan osoittajassa.
Murtolukujen kertolasku
Esim. 1
$$\frac{1}{2}\cdot\frac{1}{3}=\frac{1\cdot1}{2\cdot3}=\frac{1}{6}$$
Murtolukujen kertolaskussa osoittajat kerrotaan keskenään ja nimittäjät kerrotaan keskenään.
Esim. 2
$$3\cdot\frac{2}{7}=\frac{3}{1}\cdot\frac{2}{7}=\frac{3\cdot2}{1\cdot7}=\frac{3\cdot2}{7}=\frac{6}{7}$$
Muuta kokonaisluvut murtoluvuiksi ennen kertomista. Toisaalta, kuten yltä näkyy, näin päädytään tilanteeseen, joka on todennäköisesti alakoulussa esitetty laskusääntönä: Kokonaisluku ja murtoluvun osoittaja kerrotaan keskenään.
Esim. 3
$$\frac{2}{5}\cdot\left(-\frac{3}{8}\right)=-\frac{2\cdot3}{5\cdot8}=-\frac{6}{40}^{(2}=-\frac{3}{20}$$
Päättele etumerkki ensin.
Esim. 4
Tapa 1: Vastauksen supistaminen
$$\frac{3}{4}\cdot\frac{8}{9}=\frac{24}{36}^{(12}=\frac{2}{3}$$
Tapa 2: Tulon supistaminen
$$\frac{\overset{1}{\cancel3}}{\underset{1}{\bcancel4}}\cdot\frac{\overset{2}{\bcancel8}}{\underset{3}{\cancel{9}}}=\frac{2}{3}$$
Murtolukujen jakolasku
Ennen kuin opiskellaan murtolukujen jakolasku, kerrataan käänteisluku.
Esim. 1
$$ \begin{array}{rcl} \mathrm{Luku}&\rightarrow&\mathrm{Käänteisluku} \\ \frac{2}{3}&\rightarrow&\frac{3}{2} \\ \frac{1}{4}&\rightarrow&\frac{4}{1}=4 \\ 3=\frac{3}{1}&\rightarrow&\frac{1}{3} \\ 2\frac{1}{3}=\frac{7}{3}&\rightarrow&\frac{3}{7} \\ 0{,}7=\frac{7}{10}&\rightarrow&\frac{10}{7} \end{array} $$
Esim. 2
Mikä on luvun \(0{,}4\) käänteisluku?
Ratkaisu:
Käänteislukujen tulo on 1.
Merkitään kysyttyä käänteislukua tuntemattomalla \(x\). Tällöin $$0{,}4\cdot x=1 \iff x=\frac{1}{0{,}4}=2{,}5\mathrm{.}$$
Murtolukujen jakolasku
Murtolukujen jakolasku suoritetaan siten, että jaettava kerrotaan jakajan kääteisluvulla.
Esim. 3
$$\frac{2}{3}:\frac{3}{4}=\frac{2}{3}\cdot\frac{4}{3}=\frac{8}{9}$$
Jakolasku muutetaan kertolaskuksi ja jakaja käänteisluvuksi.
Esim. 4
$$\frac{2}{5}:3=\frac{2}{5}:\frac{3}{1}=\frac{2}{5}\cdot\frac{1}{3}=\frac{2}{5\cdot3}=\frac{2}{15}$$
Kun murtoluku jaetaan kokonaisluvulla, on kokonaisluku muutettava ensin murtoluvuksi. Kuten yllä näkyy, päädytään lopulta tilanteeseen, joka on yläkoulussa saatettu esittää laskusääntönä: Jaettavan nimittäjä kerrotaan kokonaisluvulla.
2 YHTÄLÖT
2.1 Ensimmäisen asteen yhtälö
Kun kaksi lauseketta merkitään yhtä suuriksi, saadaan yhtälö.
$$ \underbrace{3x+4}_\text{vasen puoli} = \underbrace{5x}_\text{oikea puoli} $$
Ensimmäisen asteen yhtälössä tuntemattoman \(x\) korkein asteluku (eli eksponentti) on \(1\).
Yhtälön ratkaisu eli juuri tarkoittaa tuntemattoman \(x\) paikalle sopivaa lukua, jolla yhtälön vasen ja oikea puoli ovat yhtä suuria.
Esim. 1. Ratkaisun tutkiminen.
Tutki, onko \(x=2\) yhtälön \(3x+4=5x\) ratkaisu.
Ratkaisu:
$$ \begin{array}{rcll} 3x+4&=&5x &\quad||\ x=2\\ 3\cdot 2+4&=&5 \cdot 2& \\ 6+4&=&10 &\\ 10&=&10 &\\ \end{array} $$
Vastaus: \(x=2\) on yhtälön ratkaisu.
Yhtälön ratkaiseminen tarkoittaa, että etsitään yhtälön ratkaisu. Ratkaisemisessa seuraavat toimenpiteet ovat sallittuja, koska ne säilyttävät vasemman ja oikean puolen suhteen.
- Vasemman ja oikean puolen paikat voidaan vaihtaa.
- Vasemmalle ja oikealle puolelle voidaan lisätä sama luku tai kummaltakin puolelta voidaan vähentää sama luku. Tämä voidaan merkitä siirtona yhtäsuuruusmerkin yli siten, että siirrettävän luvun tai termin etumerkki vaihtuu vastakkaiseksi.
- Vasen ja oikea puoli voidaan kertoa tai jakaa samalla luvulla.
Esim. 2
Ratkaise yhtälö \(5x-2=3x-1\).
Ratkaisu:
$$ \begin{array}{rcll} 5x-2&=&3x-1 &\quad||\ \mathrm{Siirrä.}\\ 5x-3x&=&-1+2 &\quad||\ \mathrm{Yhdistä.}\\ 2x&=&1 &\quad||\ \mathrm{Jaa.}\\ x&=&\frac{1}{2}& \\ \end{array} $$
Tarkistus:
$$ \begin{array}{rcll} 5x-2&=&3x-1 &\quad||\ x=\frac{1}{2}\\ 5 \cdot \frac{1}{2}-2&=&3 \cdot \frac{1}{2}-1 & \\ \frac{5}{2}-2&=&\frac{3}{2}-1 & \\ 2\frac{1}{2}-2&=&1\frac{1}{2}-1& \\ \frac{1}{2}&=&\frac{1}{2}& \end{array} $$
Esim. 3. Sulkeiden poistaminen.
Ratkaise yhtälö \(2(x-1)=4-(3x-1)+(x+1)\).
Ratkaisu:
$$ \begin{array}{rcll} 2(x-1)&=&4-(3x-1)+(x+1) &\quad||\ \mathrm{Poista\ sulkeet.}\\ 2x-2&=&4-3x+1+x+1 &\quad||\ \mathrm{Siirrä.}\\ 2x+3x-x&=&4+1+1+2 &\quad||\ \mathrm{Yhdistä.}\\ 4x&=&8 &\quad||\ \mathrm{Jaa.}\\ x&=&\frac{8}{4}=2& \\ \end{array} $$
Esim. 4. Nimittäjien poistaminen.
Ratkaise yhtälö \(\frac{x}{3}-\frac{1}{2}=\frac{2}{3}\).
Ratkaisu:
Tapa 1: Laventamalla.
$$ \begin{array}{rcll} \frac{x}{3}-\frac{1}{2}&=&\frac{2}{3} &\quad||\ \mathrm{Lavenna\ samannimisiksi.}\\ { ^{2)}\atop }\frac{x}{3}-{ ^{3)}\atop }\frac{1}{2}&=&{ ^{2)}\atop }\frac{2}{3} & \\ \frac{2x}{6}-\frac{3}{6}&=&\frac{4}{6} &\quad||\ \mathrm{Tarkastellaan\ vain\ osoittajia.}\\ 2x-3&=&4 &\quad||\ \mathrm{Siirrä.}\\ 2x&=&4+3 &\quad||\ \mathrm{Yhdistä.}\\ 2x&=&7& \quad||\ \mathrm{Jaa.}\\ x&=&\frac{7}{2} \end{array} $$
Tapa 2: Nimittäjät pois kertomalla.
$$ \begin{array}{rcll} \frac{x}{3}-\frac{1}{2}&=&\frac{2}{3} &\quad||\ \cdot 6\\ \overset{2}{\cancel6}\cdot\frac{x}{\underset{1}{\cancel3}}-\overset{3}{\cancel6}\cdot \frac{1}{\underset{1}{\cancel2}}&=&\overset{2}{\cancel6}\cdot \frac{2}{\underset{1}{\cancel3}} & \\ 2x-3&=&4 &\quad||\ \mathrm{Siirrä.}\\ 2x&=&4+3 &\quad||\ \mathrm{Yhdistä.}\\ 2x&=&7& \quad||\ \mathrm{Jaa.}\\ x&=&\frac{7}{2} \end{array} $$
2.2 Identtinen yhtälö
Ensimmäisen asteen yhtälöllä voi olla täsmälleen yksi ratkaisu, ei yhtään ratkaisua tai ääretön määrä ratkaisuja eli tuntemattoman \(x\) paikalle sopii mikä tahansa reaaliluku. Jos yhtälöllä ei ole ratkaisua, sanomme, että yhtälö on identtisesti epätosi. Jos ratkaisuja ovat kaikki reaaliluvut, sanomme, että yhtälö on identtisesti tosi.
Esim. 1
Ratkaise yhtälö \(2x+6=2(x+3)\).
Ratkaisu:
$$ \begin{array}{rcl} 2x+6&=&2(x+3) \\ 2x+6&=&2x+6 \\ 2x-2x&=&6-6 \\ 0&=&0 \quad \mathrm{identtisesti\ tosi} \\ \end{array} $$
Vastaus: Yhtälön ratkaisuja ovat kaikki reaaliluvut.
Esim. 2
Ratkaise yhtälö \(x+1=x\).
Ratkaisu:
$$ \begin{array}{rcl} x+1&=&x \\ x-x&=&-1 \\ 0&=&-1 \quad \mathrm{identtisesti\ epätosi} \\ \end{array} $$
Vastaus: Yhtälöllä ei ole ratkaisua.
Esim. 3
Millä vakion \(a\) arvolla yhtälöllä \(ax-3=2x+5\) ei ole ratkaisua?
Ratkaisu:
$$ \begin{array}{rcl} ax-3&=&2x+5 \\ ax-2x&=&5+3 \\ (a-2)x&=&8 \\ x&=&\frac{8}{a-2} \end{array} $$
Lukua \(\frac{8}{a-2}\) ei ole määritelty, kun \(a-2=0\) (nollalla ei voi jakaa).
$$ \begin{array}{rcl} a-2&=&0 \\ a&=&2 \\ \end{array} $$
Toisaalta jo ratkaisun toisessa vaiheessa nähdään, että yhtälöllä ei ole ratkaisua, jos yhtälö on identtisesti epätosi eli jos yhtälön vasen puoli on \(ax-2x=0 \Leftrightarrow a=2\).
Vastaus: Yhtälöllä ei ole ratkaisua, kun \(a=2\).
2.3 Yhtälöpari
Yhtälöpari muodostuu kahdesta yhtälöstä. Tunnuksena on vasemmanpuoleinen aaltosulje.
$$ \left\{ \begin{aligned} x+y&=11\\ x-y&=-3\\ \end{aligned} \right. $$
Yhtälöparin ratkaisu on lukupari \( (x,y)\), joka toteuttaa molemmat yhtälöt.
Esim. 1. Ratkaisun tutkiminen.
Tutki, onko lukupari \( (4,7)\) yhtälöparin
$$ \left\{ \begin{aligned} x+y&=11\\ x-y&=-3\\ \end{aligned} \right. $$
ratkaisu.
Ratkaisu:
Tutkitaan kumpikin yhtälö erikseen.
Ylempi yhtälö:
$$ \begin{array}{rcll} x+y&=&11 &\quad ||\ x=4, y=7 \\ 4+7&=&11 & \\ 11&=&11 &\quad \mathrm{tosi} \end{array} $$
Alempi yhtälö:
$$ \begin{array}{rcll} x-y&=&-3 &\quad ||\ x=4, y=7 \\ 4-7&=&-3 & \\ -3&=&-3 &\quad \mathrm{tosi} \end{array} $$
Vastaus: Koska lukupari \( (4,7)\) toteuttaa molemmat yhtälöt, se on yhtälöparin ratkaisu.
Esim. 2. Yhtälöparin ratkaiseminen.
Ratkaise yhtälöpari \( \left\{ \begin{aligned} 2x+4y&=-2\\ 3x+5y&=-1\\ \end{aligned} \right. \) .
Ratkaisu:
Tapa 1: Yhteenlasku- eli eliminointimenetelmä.
\( \ \ \ \left\{ \begin{aligned} 2x+4y&=-2\quad||\ \cdot 3 \\ 3x+5y&=-1\quad||\ \cdot (-2) \\ \end{aligned} \right. \)
\(
\underline{\begin{array}\ \\+\end{array}\left\{
\begin{aligned}
\cancel{6x}+12y&=-6 \\
\cancel{-6x}-10y&=2 \\
\end{aligned}
\right.}
\)
\(
\qquad \qquad \qquad 2y=-4
\)
\( \qquad \qquad \qquad \ \ y=\frac{-4}{2}=-2 \)
Sijoitetaan \(y=-2\) alkuperäisistä yhtälöistä ylempään.
\( \begin{aligned} 2x+4\cdot (-2)&=-2\\ 2x-8&=-2\\ 2x&=-2+8\\ 2x&=6\\ x&=\frac{6}{2}=3 \end{aligned} \)
Vastaus: \( \left\{ \begin{aligned} x&=3 \\ y&=-2 \\ \end{aligned} \right. \)
Tapa 2: Sijoitusmenetelmä
\( \left\{ \begin{aligned} 2x+4y&=-2\\ 3x+5y&=-1\\ \end{aligned} \right. \) .
Ratkaistaan ylempi yhtälö muuttujan \(x\) suhteen.
\( \begin{aligned} 2x+4y&=-2\\ 2x&=-2-4y\\ x&=\frac{-2-4y}{2}\\ x&=-1-2y\\ \end{aligned} \)
Sijoitetaan \(x=-1-2y\) alempaan yhtälöön ja ratkaistaan näin saatu yhtälö muuttujan \(y\) suhteen.
\( \begin{aligned} 3x+5y&=-1\\ 3(-1-2y)+5y&=-1\\ -3-6y+5y&=-1\\ -6y+5y&=-1+3\\ -y&=2\\ y&=-2\\ \end{aligned} \)
Sijoitetaan \(y=-2\) alkuperäisistä yhtälöistä ylempään.
\( \begin{aligned} 2x+4\cdot (-2)&=-2\\ 2x-8&=-2\\ 2x&=-2+8\\ 2x&=6\\ x&=\frac{6}{2}=3 \end{aligned} \)
Vastaus: \( \left\{ \begin{aligned} x&=3 \\ y&=-2 \\ \end{aligned} \right. \)
3 POTENSSIT
3.1 Potenssin määritelmä
Luvun kertominen itsellään voidaan lyhentää potenssimerkinnän avulla.
Potenssimerkintä
$$a^{x}=\underbrace{a\cdot a\cdot \ldots \cdot a}_\text{x kpl}$$
Potenssimerkinnässä kantaluku kerrotaan itsellään eksponentin osoittama määrä kertoja.
Esim. 1
$$3^{4}=3 \cdot 3 \cdot 3 \cdot 3 = 81$$
Eksponentti vaikuttaa vain välittömästi sen edessä olevaan lukuun. Muussa tapauksessa vaikutusalue määrätään sulkeilla.
Esim. 2
a) \(-3^{2}=-3\cdot 3=-9\)
b) \((-3)^2=-3\cdot (-3)=9\)
Esim. 3
a) \(\frac{3}{4}^{2}=\frac{3\ \cdot \ 3}{4}=\frac{9}{4}\)
b) \(\left(\frac{3}{4}\right)^{2}=\frac{3}{4}\cdot \frac{3}{4}=\frac{9}{16}\)
Kymmenpotenssi
Kymmenpotenssi tarkoittaa luvun kymmenen potensseja. Suuria lukuja voidaan lyhentää kymmenpotenssin avulla. Merkinnästä käytetään myös nimitystä tieteellinen lukumuoto.
$$ \begin{aligned} 10&=10^1 \\ 100&=10^2 \\ 1000&=10^3 \\ 10000&=10^4 \\ &\vdots \\ \end{aligned} $$
Esim. 1
Merkitse kymmenpotenssin avulla.
$$2\ 150\ 000=2{,}15\cdot 10^6$$
Esim. 2
Merkitse tavallisena lukuna.
$$3{,}5\cdot 10^5 = 350\ 000$$
3.2 Potenssien laskusäännöt
Samankantaisten potenssien tulo
$$ a^{m}\cdot a^{n}=a^{m+n} $$
Samankantaisten potenssien kertolaskussa eksponentit lasketaan yhteen.
Todistus
$$ a^{m}\cdot a^{n}=\underbrace{a\cdot a\cdot\ldots\cdot a}_\text{m kpl}\cdot\underbrace{a\cdot a\cdot\ldots\cdot a}_\text{n kpl}=a^{m+n} $$
Esim. 1
$$x^{5}\cdot x^{4}=x^{5+4}=x^{9}$$
Esim. 2
$$x^{4}\cdot x^{-2}=x^{4+(-2)}=x^{4-2}=x^{2}$$
Esim. 3
Tapa 1: Laskujärjestyssäännöt
$$2^{3}\cdot2^{4}=8\cdot16=128$$
Tapa 2: Potenssien laskusäännöt
$$2^{3}\cdot2^{4}=2^{3+4}=2^{7}=128$$
Samankantaisten potenssien osamäärä
$$ \frac{a^{m}}{a^{n}}=a^{m-n} $$
Samankantaisten potenssien jakolaskussa eksponentit vähennetään.
Todistus
Todistetaan tilanne, jossa luku \(m\) on suurempi kuin luku \(n\).
$$ \frac{a^{m}}{a^{n}}=\frac{\overbrace{a\cdot a\cdot\ldots\cdot a}^\text{m kpl}}{\underbrace{a\cdot a\cdot\ldots\cdot a}_\text{n kpl}}=\frac{a \cdot a \cdot \ldots \cdot a \cdot \overbrace{\cancel{a}\cdot \cancel{a}\cdot\ldots\cdot \cancel{a}}^\text{n kpl}}{\underbrace{\cancel{a}\cdot \cancel{a}\cdot\ldots\cdot \cancel{a}}_\text{n kpl}}=a^{m-n} $$
Esim. 1
$$\frac{x^{7}}{x^{3}}=x^{7-3}=x^{4}$$
Tulon potenssi
$$(ab)^n=a^{n}b^{n}$$
Kertolaskun potenssissa kukin kerrottava korotetaan erikseen potenssiin.
Todistus
$$ (ab)^{n}=\underbrace{ab\cdot ab\cdot\ldots\cdot ab}_\text{n kpl}=\underbrace{a\cdot a\cdot\ldots\cdot a}_\text{n kpl}\cdot \underbrace{b\cdot b\cdot\ldots\cdot b}_\text{n kpl}=a^{n}b^{n} $$
Esim. 1
$$(3x)^2=3^{2}x^{2}=9x^{2}$$
Esim. 2
$$2^{10}\cdot 0{,}5^{10}=(2\cdot 0{,}5)^{10}=1^{10}=1$$
Osamäärän potenssi
$$\left(\frac{a}{b}\right)^n=\frac{a^{n}}{b^{n}}$$
Jakolaskun potenssissa jaettava ja jakaja korotetaan erikseen potenssiin.
Todistus
$$ \left(\frac{a}{b}\right)^{n}=\underbrace{\frac{a}{b}\cdot \frac{a}{b}\cdot \ldots\cdot\frac{a}{b}}_\text{n kpl}=\frac{\overbrace{a\cdot a\cdot\ldots\cdot a}^\text{n kpl}}{\underbrace{b\cdot b\cdot\ldots\cdot b}_\text{n kpl}}=\frac{a^{n}}{b^{n}} $$
Esim. 1
$$\left(\frac{x}{2}\right)^4=\frac{x^{4}}{2^{4}}=\frac{x^{4}}{16}$$
Esim. 2
$$\frac{2^{6}}{0{,}2^{6}}=\left(\frac{2}{0{,}2}\right)^{6}=10^{6}=1\ 000\ 000$$
Potenssin potenssi
$$\left(a^m\right)^n=a^{m\ \cdot \ n}$$
Todistus
$$ \begin{aligned} \left(a^m\right)^n&=\underbrace{a^{m}\cdot a^{m}\cdot \ldots \cdot a^{m}}_\text{n kpl}\\ &=a\underbrace{^{m+m+\dots+m}}_\text{n kpl}\\ &=a^{m\ \cdot \ n} \end{aligned} $$
Esim. 1
$$\left(x^{2}\right)^4=x^{2\ \cdot\ 4}=x^{8}$$
Esim. 2
Tapa 1: Laskujärjestys
$$\left(2^{3}\right)^2=8^{2}=64$$
Tapa 2: Potenssin potenssi
$$\left(2^{3}\right)^2=2^{3\ \cdot\ 2}=2^{6}=64$$
Huom.
\(2^{3^{2}}=2^9=512\) (Ei ole potenssin potenssi!)
Esim. 3
$$\left(\frac{4x^{3}}{5y}\right)^{2}=\frac{4^{2}\left(x^{3}\right)^{2}}{5^{2}y^{2}}=\frac{16x^{3\ \cdot\ 2}}{25y^{2}}=\frac{16x^{6}}{25y^{2}}$$
3.3 Eksponenttina nolla tai negatiivinen luku
Eksponenttina nolla
$$a^0=1$$
Luku potenssiin nolla on yksi.
Perustelu
Lasketaan kahdella tavalla osamäärä \(\frac{a^n}{a^n}\).
Tapa 1: Supistaminen.
$$\frac{a^n}{a^n}=1$$
Luku jaettuna itsellään on 1.
Tapa 2: Samankantaisten potenssien osamäärä.
$$\frac{a^n}{a^n}=a^{n-n}=a^0$$
Yksikäsitteisyyden nojalla tulokset on samaistettava ja täten on oltava \(a^0=1\).
Esim. 1
a) \(2023^{0}=1\)
b) \(x^{0}=1\)
c) \(\left(\frac{7x^{5}}{9xy^{2}}\right)^{0}=1\)
Negatiivinen eksponentti
$$a^{-n}=\left(\frac{1}{a}\right)^n$$
Korotettaessa lukua negatiiviseen potenssiin kantaluvusta tehdään käänteisluku ja eksponentista vastaluku.
Perustelu
Lasketaan kahdella tavalla osamäärä \(\frac{a^m}{a^n}\), kun luku \(m\) on pienempi kuin luku \(n\).
Tapa 1: Supistaminen.
$$ \begin{aligned} \frac{a^m}{a^n}&=\frac{\overbrace{a\cdot a\cdot\ldots\cdot a}^\text{m kpl}}{\underbrace{a\cdot a\cdot\ldots\cdot a}_\text{n kpl}}\\ &=\frac{\overbrace{\cancel{a}\cdot \cancel{a}\cdot\ldots\cdot \cancel{a}}^\text{m kpl}}{a \cdot a \cdot \ldots \cdot a \cdot \underbrace{\cancel{a}\cdot \cancel{a}\cdot\ldots\cdot \cancel{a}}_\text{m kpl}}\\ &=\frac{1}{a^{n-m}}\\ &=\frac{1}{a^{-(m-n)}}=\left(\frac{1}{a}\right)^{-(m-n)}, \end{aligned} $$
missä \(n-m>0\) ja sen vastaluku \(m-n<0\).
Tapa 2: Samankantaisten potenssien osamäärä.
$$\frac{a^m}{a^n}=a^{m-n},$$
missä \(m-n<0\).
Yksikäsitteisyyden nojalla tulokset on samaistettava ja täten on oltava \(a^{m-n}=\left(\frac{1}{a}\right)^{-(m-n)}\).
Lukemisen helpottamiseksi merkitään vielä \(m-n=-p\), jolloin voidaan kirjoittaa \(a^{-p}=\left(\frac{1}{a}\right)^{-(-p)}=\left(\frac{1}{a}\right)^{p}\).
Esim. 1
a) \(3^{-1}=\left(\frac{1}{3}\right)^{1}=\frac{1^{1}}{3^{1}}=\frac{1}{3}\)
b) \(\left(\frac{3}{4}\right)^{-2}=\left(\frac{4}{3}\right)^{2}=\frac{4^{2}}{3^{2}}=\frac{16}{9}\)
c) \((5x)^{-2}=\left(\frac{1}{5x}\right)^{2}=\frac{1^{2}}{(5x)^{2}}=\frac{1}{5^{2}x^{2}}=\frac{1}{25x^{2}}\)
Esim. 2
Merkitse kantaluvun 2 potenssina.
a) \(16=2^{4}\)
b) \(0{,}5=\frac{1}{2}=2^{-1}\)
Kymmenpotenssi ja negatiivinen eksponentti
Hyvin lähellä nollaa olevia lukuja voidaan lyhentää kymmenpotenssin avulla käyttämällä negatiivisia eksponentteja.
$$ \begin{array}{lccl} 1&&&=10^0 \\ 0{,}1&=&\frac{1}{10}&=10^{-1} \\ 0{,}01&=&\frac{1}{100}&=10^{-2} \\ 0{,}001&=&\frac{1}{1000}&=10^{-3} \\ 0{,}0001&=&\frac{1}{10000}&=10^{-4} \\ &&\vdots& \\ \end{array} $$
Esim. 1
Merkitse kymmenpotenssin avulla.
a) \(0{,}005=5\cdot 0{,}001=5\cdot\frac{1}{1000}=5\cdot10^{-3}\)
b) \(0{,}000\ 002\ 4=2{,}4\cdot 10^{-6}\)
Esim. 2
Merkitse tavallisena lukuna.
\(3{,}17\cdot 10^{-4}=0{,}000\ 317\)
4 JUURET
4.1 Neliöjuuri
Neliöjuuri on laskutoimitus, jonka tulos ilmoittaa vastauksen kysymykseen, mikä luku on kerrottava itsellään, että saadaan juurimerkin alla oleva luku.
Esim. 1
\(\sqrt{16}=4\), koska \(4^{2}=4\cdot 4=16\).
Neliöjuuren määritelmä
\(\sqrt{a}=b\), kun
1) \(b\geq 0\) ja
2) \(b^{2}=a\)
Siis luvun \(a\) neliöjuuri on (1) epänegatiivinen luku \(b\), jonka (2) toinen potenssi on luku \(a\).
Toisin sanoen kohta (1) tarkoittaa, että neliöjuuren arvo on aina positiivinen luku.
Määrittelyehto
Neliöjuuri \(\sqrt{a}\) on määritelty vain silloin, kun luku \(a\geq0\)
Neliöjuuri on luvun neliön eli toisen potenssin vastalasku. Tämä seuraa neliöjuuren määritelmän kohdasta (2) ja voidaan muotoilla matemaattisin merkein: $$\left(\sqrt{a}\right)^{2}=a.$$
Toisin sanoen neliöjuurimerkin alla olevan luvun on oltava nolla tai positiivinen, että laskutoimitus on määritelty.
Esim. 2
Laske.
a) \(\sqrt{49}\)
b) \(\sqrt{0{,}04}\)
c) \(\sqrt{\frac{1}{9}}\).
d) \(\sqrt{-4}\)
e) \(-\sqrt{4}\)
a) \(\sqrt{49}=7\), koska \(7^{2}=49\).
b) \(\sqrt{0{,}04}=0{,}2\), koska \(0{,}2^{2}=0{,}2\cdot 0{,}2=0,04\).
c) \(\sqrt{\frac{1}{9}}=\frac{1}{3}\), koska \(\left(\frac{1}{3}\right)^{2}=\frac{1}{3}\cdot \frac{1}{3}=\frac{1}{9}\).
d) \(\sqrt{-4}\) Ei ole määritelty reaalilukujen joukossa!
e) \(-\sqrt{4}=-2\) Tarkoittaa luvun \(4\) neliöjuuren vastalukua.
Esim. 3
Laske luvun \(2\) neliöjuuri. Anna vastaus tarkkana arvona ja likiarvona kahden desimaalin tarkkuudella.
\(\underbrace{\sqrt{2}}_\text{tarkka arvo}\approx \underbrace{1{,}41}_\text{likiarvo}\)
Laskujärjestys
Esim. 4
Laske.
\(\sqrt{16+9}\)
\(\sqrt{16+9}=\sqrt{25}=5\)
Huom.
Neliöjuurimerkin alla olevat laskutoimitukset lasketaan ennen neliöjuuren ottamista ikään, kuin neliöjuurimerkin alla olevat laskutoimitukset olisivat sulkeissa.
Esim. 5
Laske.
\(\sqrt{16}+\sqrt{9}\)
\(\sqrt{16}+\sqrt{9}=4+3=7\)
Huom.
Neliöjuuret otetaan ennen neliöjuurimerkin ulkopuolella olevien laskutoimitusten laskemista.
Neliöyhtälö
Muotoa \(x^{2}=y\) olevaa potenssiyhtälöä kutsutaan neliöyhtälöksi.
Neliöyhtälö ratkaistaan neliöjuuren avulla.
Esim. 1
Ratkaise yhtälö \(x^{2}=36.\)
$$ \begin{aligned} x^{2}&=36 \quad||\ \sqrt{} \\ \sqrt{x^{2}}&=\sqrt{36} \\ x&=6 \quad \mathrm{tai}\quad x=-6 \end{aligned} $$
Vaikka neliöjuuren arvo on aina positiivinen luku, voi neliöyhtälöllä olla yksi, kaksi tai ei yhtään ratkaisua, koska yhtälön voi toteuttaa myös negatiivinen luku (neliöjuuren arvon vastaluku). Yksi ratkaisu neliöyhtälöllä on tilanteessa \(x^{2}=0 \Leftrightarrow x=0\).
Vaillinainen 2. asteen polynomiyhtälö
Muotoa \(ax^{2}+c=0\) oleva vaillinainen toisen asteen polynomiyhtälö voidaan muokata neliöyhtälöksi ja ratkaista neliöjuuren avulla.
Esim. 2
Ratkaise yhtälö \(2x^{2}-18=0.\)
$$ \begin{aligned} 2x^{2}-18&=0 \\ 2x^{2}&=18 \quad||:2 \\ x^{2}&=9\quad\ \ ||\ \sqrt{} \\ x&=3 \quad \mathrm{tai}\quad x=-3 \end{aligned} $$
Esim. 3*
Ratkaise yhtälö \(5x^{2}+2x=2(x^{2}+x+6).\)
$$ \begin{aligned} 5x^{2}+2x&=2(x^{2}+x+6) \\ 5x^{2}+2x&=2x^{2}+2x+12 \\ 5x^{2}+\cancel{2x}-2x^{2}-\cancel{2x}&=12 \\ 3x^{2}&=12 \quad ||:3 \\ x^{2}&=4 \quad\ \ ||\ \sqrt{}\\ x&=2 \quad \mathrm{tai}\quad x=-2 \end{aligned} $$
4.2 Kuutiojuuri
Kuutiojuuri (eli kolmas juuri) on laskutoimitus, jonka tulos ilmoittaa vastauksen kysymykseen, mikä luku on kerrottava itsellään kolmesti, että saadaan juurimerkin alla oleva luku.
Esim. 1
a) \(\sqrt[3]{8}=2\), koska \(2^{3}=2\cdot 2\cdot 2 =8\).
b) \(\sqrt[3]{-8}=-2\), koska \((-2)^{3}=-2\cdot (-2)\cdot (-2) =-8\).
Kuutiojuuren määritelmä
\(\sqrt[3]{a}=b\), kun
\(b^{3}=a\)
Siis luvun \(a\) kuutiojuuri on luku \(b\), jonka kolmas potenssi on luku \(a\).
Määrittelyehto
Kuutiojuuri \(\sqrt[3]{a}\) on määritelty kaikilla luvuilla \(a\).
Kuutiojuuren määritelmästä seuraa, että kuutiojuuren arvo voi olla positiivinen, nolla tai negatiivinen sen mukaan, onko juurrettava positiivinen, nolla tai negatiivinen. Toisin sanoen kuutiojuuren arvon etumerkki on aina sama kuin juurrettavan etumerkki.
Kuutiojuuri on luvun kuution eli kolmannen potenssin vastalasku. Tämä seuraa kuutiojuuren määritelmästä ja voidaan muotoilla matemaattisin merkein: $$\left(\sqrt[3]{a}\right)^{3}=a.$$
Esim. 2
Laske.
a) \(\sqrt{27}\)
b) \(\sqrt{-0{,}027}\)
a) \(\sqrt{27}=7\), koska \(3^{3}=3\cdot3\cdot3=27\).
b) \(\sqrt{-0{,}027}=-0{,}3\), koska \((-0{,}3)^{3}=-0{,}3\cdot(-0{,}3)\cdot(-3{,}3)=-0,027\).
Esim. 3
Laske luvun \(54\) kuutiojuuri. Anna vastaus tarkkana arvona ja likiarvona kahden desimaalin tarkkuudella.
\(\sqrt[3]{54}=\underbrace{3\cdot \sqrt[3]{2}}_\text{tarkka arvo}\approx \underbrace{3{,}78}_\text{likiarvo}\)
Kuutioyhtälö
Muotoa \(x^{3}=y\) olevaa potenssiyhtälöä kutsutaan kuutioyhtälöksi.
Kuutioyhtälö ratkaistaan kuutiojuuren avulla.
Esim. 1
Ratkaise yhtälö \(x^{3}=-27.\)
$$ \begin{aligned} x^{3}&=-27 \quad||\ \sqrt[3]{} \\ \sqrt[3]{x^{3}}&=\sqrt[3]{-27} \\ x&=-3 \end{aligned} $$
Vaillinainen 3. asteen polynomiyhtälö
Muotoa \(ax^{3}+d=0\) oleva vaillinainen kolmannen asteen polynomiyhtälö voidaan muokata kuutioyhtälöksi ja ratkaista kuutiojuuren avulla.
Esim. 2
Ratkaise yhtälö \(2x^{3}-250=0.\)
$$ \begin{aligned} 2x^{3}-250&=0 \\ 2x^{3}&=250 \quad||:2 \\ x^{3}&=125\quad||\ \sqrt[3]{} \\ x&=5 \end{aligned} $$
Esim. 3*
Ratkaise yhtälö \((x-1)^{3}=27.\)
$$ \begin{aligned} (x-1)^{3}&=27 \quad ||\ \sqrt[3]{}\\ x-1&=3 \\ x&=3+1=4 \end{aligned} $$
5 FUNKTIOT
5.1 Funktio
Määritelmä
Funktio on sääntö, joka yhdistää jokaisen (lähtö)joukon \(X\) alkion täsmälleen yhteen (maali)joukon \(Y\) alkioon.
Funktioilla voidaan esittää riippuvuuksia. Esimerkiksi kahden muuttujan yhtälöllä voidaan esittää, miten muuttujan \(y\) arvo riippuu muuttujan \(x\) arvosta.
Esim. 1
| \(\mathbf{x}\) | \(\mathbf{y=x+3}\) |
|---|---|
| \(0\) | \(y=0+3=3\) |
| \(1\) | \(y=1+3=4\) |
| \(2\) | \(y=2+3=5\) |
| \(\vdots\) | \(\vdots\) |
Funktiomerkintä
$$y=f(x)$$
Muuttuja \(y\) korvataan funktion tapauksessa yleensä funktiomerkinnällä \(f(x)\). Merkinnällä voidaan toisaalta tarkoittaa funktion arvoa muuttujan \(x\) arvolla, toisaalta lyhentää funktion lauseketta.
Esim. 1
Merkintä \(f(2)=5\) tarkoittaa, että muuttujan arvolla \(x=2\) funktio \(f\) saa arvon \(y=5\).
Esim. 2
Merkintä \(h(a)=2a-1\) tarkoittaa, että funktion \(h\) lauseke on \(2a-1\) ja muuttujakirjaimena on \(a\).
Funktion arvon laskeminen
Esim. 1
Laske funktion \(f(x)=3x-2\) arvo kohdassa \(x=-1\).
$$ \begin{aligned} f(-1)&=3\cdot(-1)-2\\ &=-3-2\\ &=-5 \end{aligned} $$
Esim. 2
Funktio \(f(x)=4x^{2}\). Laske \(f(-2)\).
$$ \begin{aligned} f(-2)&=4\cdot(-2)^{2}\\ &=4\cdot 4\\ &=16 \end{aligned} $$
Muuttujan arvon laskeminen
Esim. 1
Millä muuttujan \(x\) arvolla funktio \(f(x)=2x-3\) saa arvon 11?
$$ \begin{aligned} 2x-3&=11\\ 2x&=11+3\\ 2x&=14\\ x&=\frac{14}{2}=7 \end{aligned} $$
Esim. 2
Millä muuttujan \(x\) arvolla funktiot \(f(x)=3x-2\) ja \(g(x)=2x-3\) saavat saman arvon?
$$ \begin{aligned} f(x)&=g(x)\\ 3x-2&=2x-3\\ 3x-2x&=-3+2\\ x&=-1\\ \end{aligned} $$
5.2 Funktion kuvaaja
Esim. 1
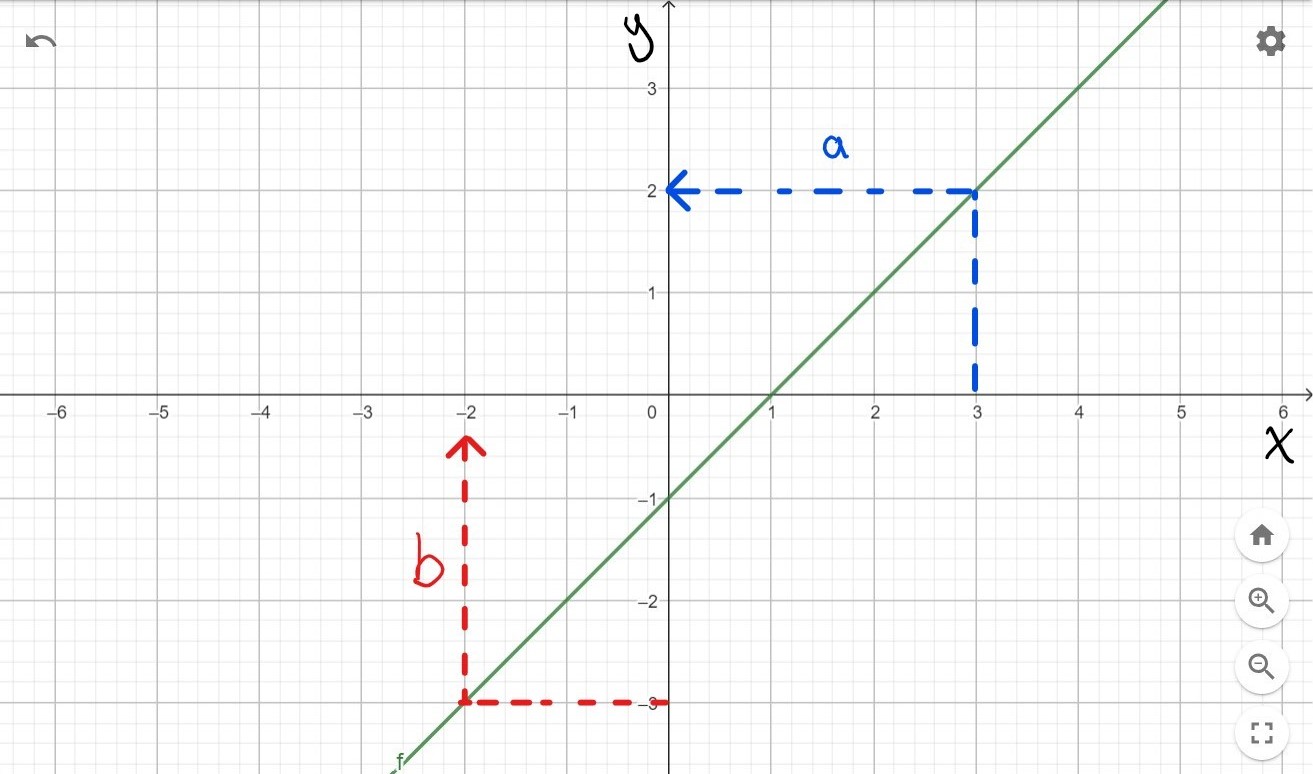
Piirrä geometriaohjelmalla funktion \(f(x)=x-1\) kuvaaja. Määritä kuvaajan perusteella
a) funktion \(f\) arvo kohdassa \(x=3\)
b) se muuttujan \(x\) arvo, jolla funktion \(f\) arvo on \(y=-3\).
Vastaus:
a) Funktion arvo on \(y=2\) (tai lyhyesti \(f(3)=2\)).
b) Muuttujan arvo on \(x=-2\).
Esim. 2
Piirrä geometriaohjelmalla funktion \(g(x)=\frac{1}{4}x^{2}-6\) kuvaaja. Määritä kuvaajan perusteella
a) funktion \(g\) arvo kohdassa \(x=4\)
b) ne muuttujan \(x\) arvot, joilla funktion \(g\) arvo on \(y=3\).
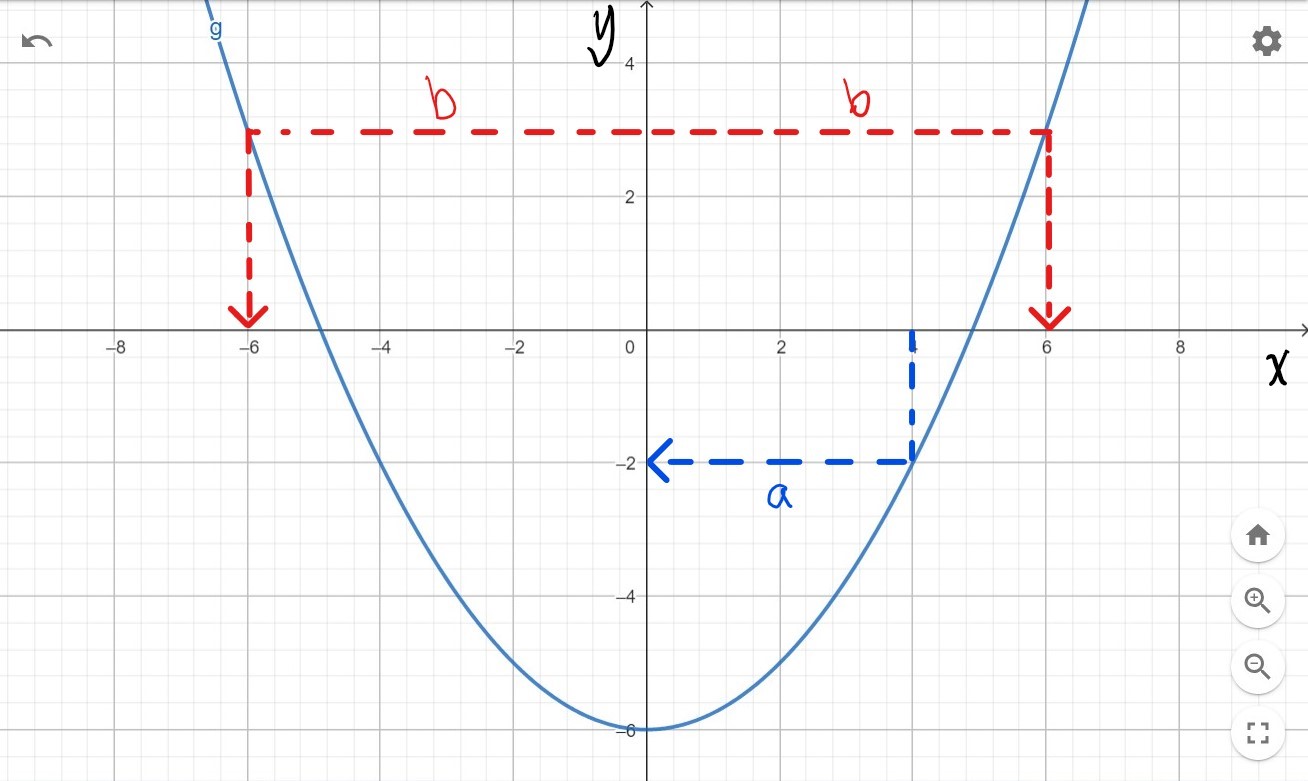
Vastaus:
a) Funktion arvo on \(y=-2\) (tai lyhyesti \(f(4)=-2\)).
b) Muuttujan arvot ovat \(x=-6\) ja \(x=6\).
Esim. 3
Piirrä geometriaohjelmalla funktion \(g(x)=\frac{1}{4}x^{2}-6\) kuvaaja. Määritä kuvaajan perusteella
a) funktion \(g\) nollakohdat (eli funktio saa arvon \(y=0\), kuvaaja leikkaa \(x\)-akselin)
b) ne muuttujan \(x\) arvot, joilla funktion \(g\) arvo on positiivinen (eli \(y> 0\), kuvaaja kulkee \(x\)-akselin yläpuolella)
c) ne muuttujan \(x\) arvot, joilla funktion \(g\) arvo on negatiivinen (eli \(y< 0\), kuvaaja kulkee \(x\)-akselin alapuolella).
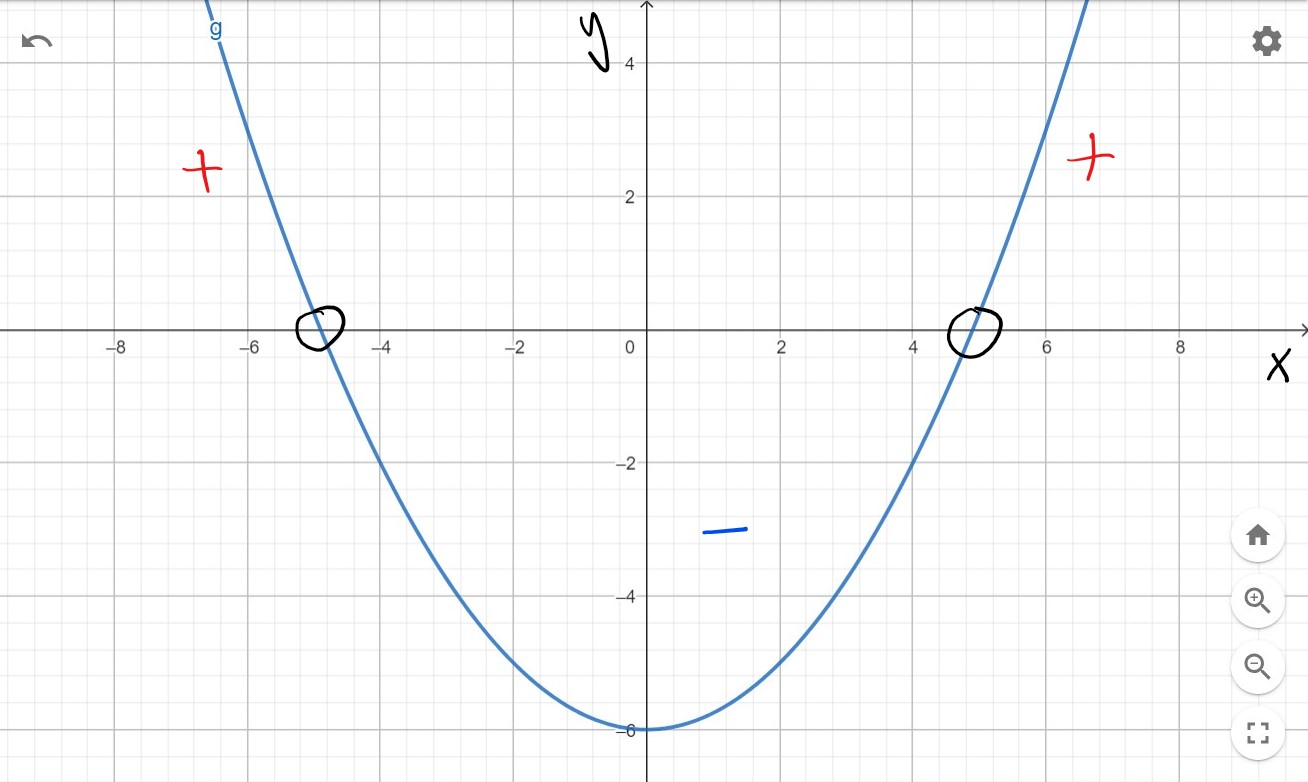
Vastaus:
a) \(x\approx -4{,}9\) ja \(x\approx 4{,}9\).
b) \(x< -4{,}9\) tai \(x> 4{,}9\).
c) \( -4{,}9 < x < 4{,}9 \).
Esim. 4
Piirrä geometriaohjelmalla funktioiden \(f(x)=x-1\) ja \(g(x)=\frac{1}{4}x^{2}-6\) kuvaajat. Määritä kuvaajien perusteella, millä muuttujan \(x\) arvoilla funktiot \(f\) ja \(g\) saavat saman arvon eli \(f(x)=g(x)\)?
Vastaus: \(x\approx -2{,}9\) ja \(x\approx 6{,}9\).
Esim. 5
Piirrä geometriaohjelmalla funktion \(f(x)=x^{2}\) kuvaaja. Määritä kuvaajan perusteella yhtälön
a) \(x^{2}=4\) ratkaisu
b) \(x^{2}=8\) ratkaisu yhden desimaalin tarkkuudella.
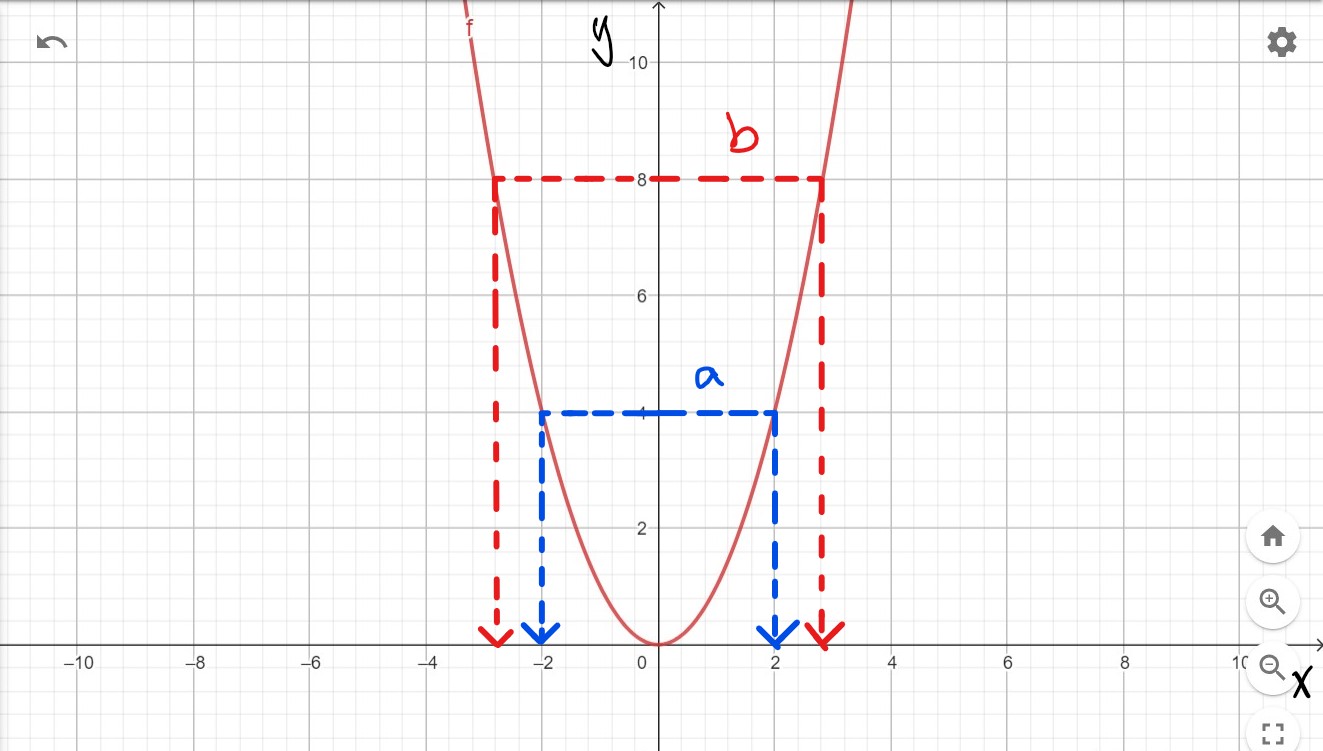
Vastaus:
a) \(x=-2\) ja \(x=2\).
b) \(x\approx -2{,}8\) ja \(x\approx 2{,}8\).
6 PROSENTIT
6.1 Prosentti
Prosentti
Yksi prosentti tarkoittaa yhtä sadasosaa.
$$1\ \%=\frac{1}{100}=0{,}01$$
Prosenttiluku muunnetaan desimaaliluvuksi jakamalla luvulla \(100\).
Esim. 1
Muunna desimaaliluvuksi.
a) \(37\ \%=0{,}37\)
b) \(105\ \%=1{,}05\)
c) \(2{,}1\ \%=0{,}021\)
Desimaaliluku muunnetaan prosenttiluvuksi kertomalla luvulla \(100\).
Esim. 2
Muunna prosenttiluvuksi.
a) \(0{,}24=24\ \%\)
b) \(3{,}5=350\ \%\)
c) \(0{,}019=1{,}9\ \%\)
Prosenttiluvun laskeminen
$$\text{prosenttiluku}\ p\ \%=\frac{\text{prosenttiarvo}\ a}{\text{perusarvo}\ b}\cdot 100\ \%$$
Prosenttiluvun laskeminen tuottaa vastauksen kysymykseen, kuinka monta prosenttia luku \(a\) on luvusta \(b\). Luvusta \(a\) käytetään nimitystä prosenttiarvo ja luvusta \(b\) perusarvo. Perusarvo on luku joka vastaa sadan prosentin kokonaisuutta.
Esim. 1
Koripallon alkuperäinen hinta oli 40 euroa. Tarjouksessa se maksoi 8 euroa vähemmän. Kuinka monta prosenttia alennus oli alkuperäisestä hinnasta?
\(\displaystyle{\frac{8\ \unicode{0x20AC}}{40\ \unicode{0x20AC}}=0{,}2=20\ \%}\)
Vastaus: Alennus oli \(20\ \%\) alkuperäisestä hinnasta.
Prosenttiarvon laskeminen
1) \(\quad\displaystyle{\frac{\text{prosenttiluku}\ p\ \%}{100\ \%}=\text{prosenttikerroin}}\)
2) \(\quad\text{prosenttikerroin}\cdot \text{perusarvo}\ b=\text{prosenttiarvo}\ a\)
Prosenttiarvon laskeminen tuottaa vastauksen kysymykseen, kuinka paljon on \(p\ \%\) perusarvosta \(b\)?"
Esim. 1
Lindan kuukausipalkka on 3 200 euroa. Hänen verokortissaan määritelty ennakonpidätysprosentti on 20 %. Kuinka paljon ennakonpidätys on euroina?
\(20\ \%=0{,}2\)
\(0{,}2\cdot 3\ 200\ \unicode{0x20AC}=640\ \unicode{0x20AC}\)
Vastaus: Ennakonpidätys on \(640\ \unicode{0x20AC}\).
Esim. 2*
Eräällä biologian opintojaksolla tutkittiin merivesien erilaisia suolapitoisuuksia. Opettajalla oli itse kerätyt näytteet vettä Atlantin valtamerestä (suolapitoisuus 3,7 %) ja Itämerestä (suolapitoisuus 0,7 %). Opiskelijalta sekoittui 500 g Atlantin vettä ja 200 g Itämeren vettä. Mikä oli seoksen suolapitoisuus?
Uusi nestemäärä:
\(500\ \text{g} + 200\ \text{g} =700\ \text{g}\)
Uusi suolamäärä:
\(0{,}037\cdot500\ \text{g} + 0{,}007\cdot 200\ \text{g} =19{,}9\ \text{g}\)
Seoksen suolapitoisuus:
\(\displaystyle{\frac{19{,}9\ \text{g}}{700\ \text{g}}=0{,}028\ 42\approx0{,}028=2{,}8\ \%}\)
Vastaus: Seoksen suolapitoisuus on \(2{,}8\ \%\).
Perusarvon laskeminen
Prosenttiarvon laskukaavasta muodostetaan yhtälö.
$$\text{prosenttikerroin}\cdot \text{perusarvo}\ b=\text{prosenttiarvo}\ a$$
Perusarvo ratkaistaan yhtälöstä.
$$\text{perusarvo}\ b=\frac{\text{prosenttiarvo}\ a}{\text{prosenttikerroin}}$$
Perusarvon laskeminen tuottaa vastauksen kysymykseen, mikä on perusarvo \(b\), jos \(p\ \%\) tuntemattomasta perusarvosta \(b\) on tunnettu prosenttiarvo \(a\).
Esim. 1
Liuos sisältää 15 prosenttia painostaan suolaa. Kuinka paljon liuosta on, kun siinä on 90 g suolaa?
\(15\ \%=0{,}15\)
\( \begin{aligned} 0{,}15\cdot x&=90\ \text{g}\\ x&=\displaystyle{\frac{90\ \text{g}}{0{,}15}=600\ \text{g}} \end{aligned} \)
Vastaus: Liuosta on \(600\ \text{g}\).
Esim. 2 *
Ostaessasi auton osamaksulla, joudut maksamaan 20 prosenttia auton hinnasta käsirahana. Mitä auto maksaa, jos maksettavaa jää 13 600 euroa?
\(100\ \% - 20\ \% =80\ \%=0{,}8\)
\( \begin{aligned} 0{,}8\cdot x&=13\ 600\ \unicode{0x20AC}\\ x&=\displaystyle{\frac{13\ 600\ \unicode{0x20AC}}{0{,}8}=17\ 000\ \unicode{0x20AC}} \end{aligned} \)
Vastaus: Auto maksaa \(17\ 000\ \unicode{0x20AC}\).
6.2 Muutos- ja vertailuprosentti
Vertailuprosentti
$$\text{vertailuprosentti}=\frac{\text{erotus}}{\text{vertailuarvo}}\cdot 100\ \%$$
Esim. 1
Manute Bol ja Tyrone Bogues ovat molemmat entisiä NBA-pelaajia. Bol on 231 cm pitkä ja Bogues 160 cm.
a) Kuinka monta prosenttia Bol on pidempi kuin Bogues?
b) Kuinka monta prosenttia Bogues on lyhyempi kuin Bol?
a) Vertailuarvona Boguesin pituus:
\(\begin{align} \displaystyle{\frac{231-160}{160}}&=\displaystyle{\frac{71}{160}}\\ &\approx0{,}44\\ &=44\ \% \end{align}\)
Vastaus: Bol on \(44\ \%\) pidempi.
b) Vertailuarvona Bolin pituus:
\(\begin{align} \displaystyle{\frac{231-160}{231}}&=\displaystyle{\frac{71}{231}}\\ &\approx0{,}31\\ &=31\ \% \end{align}\)
Vastaus: Bogues on \(31\ \%\) lyhyempi.
Muutosprosentti
$$\text{muutosprosentti}=\frac{\text{muutos}}{\text{alkuperäinen arvo}}\cdot 100\ \%$$
Esim. 1
Bensiinin litrahinta nousi 1,94 eurosta 2,02 euroon. Kuinka monta prosenttia hinta nousi?
\(\begin{align} \displaystyle{\frac{2{,}02\ \unicode{0x20AC}-1{,}94\ \unicode{0x20AC}}{1{,}94\ \unicode{0x20AC}}}&=\displaystyle{\frac{0{,}08\ \unicode{0x20AC}}{1{,}94\ \unicode{0x20AC}}}\\ &=0{,}04123\\ &\approx0{,}041\\ &=4{,}1\ \% \end{align}\)
Vastaus: Bensiinin hinta nousi \(4{,}1\ \%\).
Esim. 2
Puolueen kannatus laski 22 prosentista 19 prosenttiin.
a) Kuinka monta prosenttiyksikköä kannatus laski?
b) Kuinka monta prosenttia kannatus laski?
a) Muutos prosenttiyksikköinä:
\(22-19=3\)
Vastaus: Kannatus nousi \(3\) prosenttiyksikköä.
b) Muutosprosentti:
\(\begin{align} \displaystyle{\frac{22-19}{22}}&=\displaystyle{\frac{3}{22}}\\ &=0{,}13636\ldots\\ &\approx0{,}136\\ &=13{,}6\ \% \end{align}\)
Vastaus: Kannatus laski \(13{,}6\ \%\).
Esim. 3*
Liikuntapalvelujen arvonlisävero nousi 10 prosentista 14 prosenttiin.
a) Kuinka monta prosenttiyksikköä arvonlisävero nousi?
b) Kuinka monta prosenttia liikuntapalveluista maksettava vero nousi?
a) Muutos prosenttiyksikköinä:
\(14-10=4\)
Vastaus: Arvonlisävero nousi \(4\) prosenttiyksikköä.
b) Merkitään liikuntapalvelun hintaa yleisesti muuttujalla \(a\).
Vanha veron määrä: \(0{,}1a\)
Uusi veron määrä: \(0{,}14a\)
Muutosprosentti:
\(\begin{align} \displaystyle{\frac{0{,}14a-0{,}1a}{0{,}1a}}&=\displaystyle{\frac{0{,}04a}{0{,}1a}}\\ &=0{,}4\\ &=40\ \% \end{align}\)
Vastaus: Veron määrä nousi \(40\ \%\).
6.3 Muuttuva arvo
Esim. 1
Kuinka moninkertaiseksi tuotteen hinta muuttuu alkuperäiseen hintaan verrattuna, jos hintaa
a) nostetaan 100 %
b) nostetaan 200 %
c) nostetaan 50 %
d) lasketaan 50 %
a) \(100\ \%+100\ \%=200\ \%=2\)
Vastaus: Kaksinkertaiseksi.
b) \(100\ \%+200\ \%=300\ \%=3\)
Vastaus: Kolminkertaiseksi.
c) \(100\ \%+50\ \%=150\ \%=1{,}5\)
Vastaus: 1,5- eli puolitoistakertaiseksi.
d) \(100\ \%-50\ \%=50\ \%=0{,}5\)
Vastaus: 0,5-kertaiseksi eli hinta puolittuu.
Esim. 2
Koripallo maksaa 75 euroa. Sen hintaa nostetaan 5 %. Laske uusi hinta.
\(100\ \%+5\ \%=105\ \%=1{,}05\)
\(1{,}05\cdot 75\ \unicode{0x20AC}=78{,}75\ \unicode{0x20AC}\)
Vastaus: Uusi hinta on \(78{,}75\ \unicode{0x20AC}\).
Esim. 3
120 euron tennismaila myydään 15 prosentin alennuksella. Laske alennettu hinta.
\(100\ \%-15\ \%=85\ \%=0{,}85\)
\(0{,}85\cdot 120\ \unicode{0x20AC}=102\ \unicode{0x20AC}\)
Vastaus: Alennettu hinta on \(102\ \unicode{0x20AC}\).
Esim. 4
Tuotteen hinta nousi ensin 10 % ja sitten 20 %. Kuinka monta prosenttia hinta nousi yhteensä?
Merkitään tuotteen alkuperäistä hintaa \(a\).
Hinta 1. korotuksen jälkeen:
\(100\ \%+10\ \%=110\ \%=1{,}1\)
\(1{,}1a\)
Hinta 2. korotuksen jälkeen:
\(100\ \%+20\ \%=120\ \%=1{,}2\)
\(1{,}2\cdot 1{,}1a=1{,}32a\)
Muutosprosentti:
\(\begin{align} \displaystyle{\frac{1{,}32a-a}{a}}&=\displaystyle{\frac{0{,}32\cancel{a}}{\cancel{a}}}\\ &=0{,}32\\ &=32\ \% \end{align}\)
Vastaus: Hinta nousi yhteensä \(32\ \%\).
7 VERRANNOLLISUUS
7.1 Suoraan verrannollisuus
Jos suureet A ja B ovat suoraan verrannollisia, niin ne muuttuvat samassa suhteessa samaan suuntaan. Esimerkiksi jos suure A kaksinkertaistuu, niin myös suure B kaksinkertaistuu.
Esim. 1. Banaanien kilohinta.
Banaanien hinta on suoraan verrannollinen banaanien määrään (massaan).
| massa (kg) | hinta (€) |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | 8 |
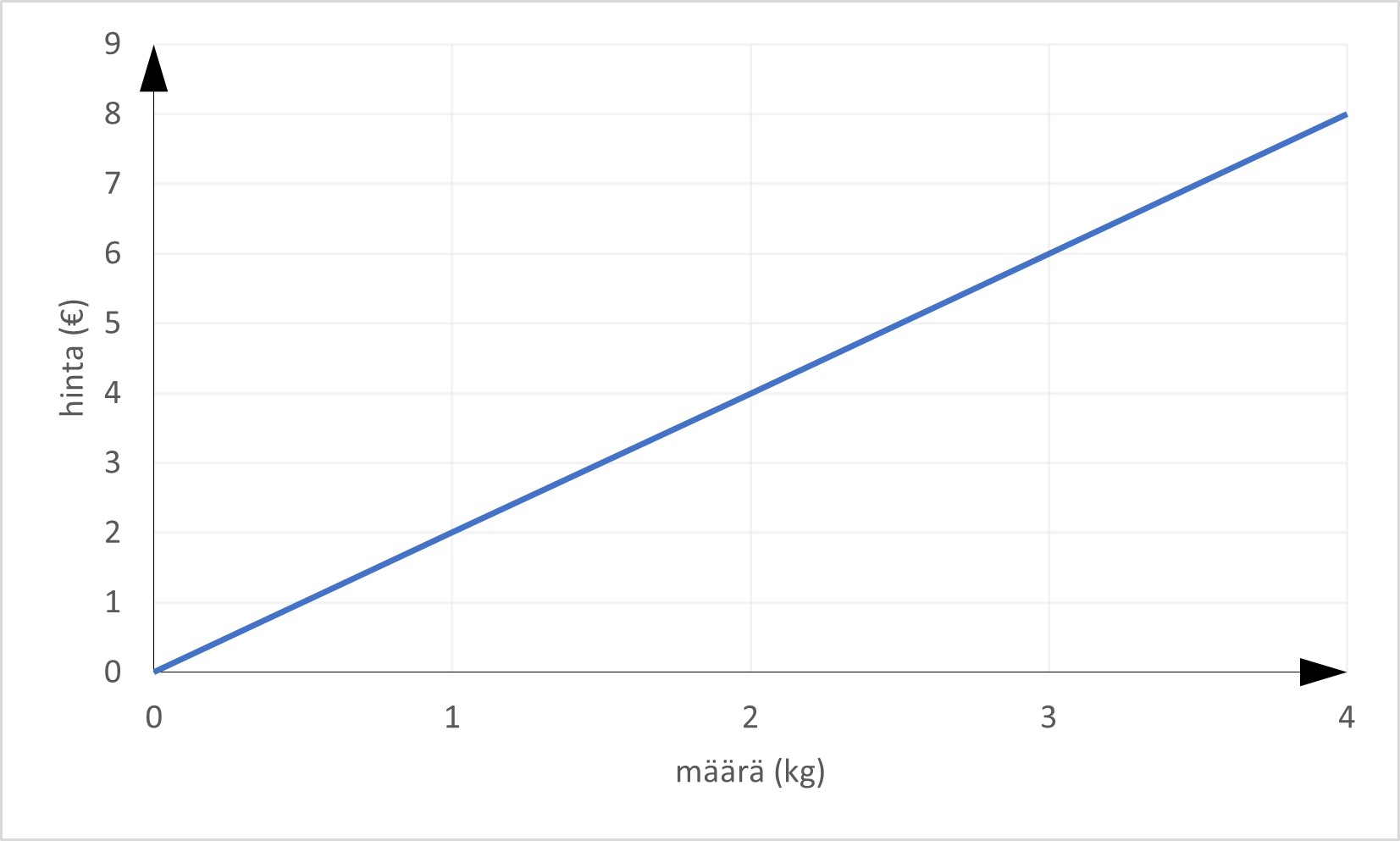
Suoraan verrannollisen funktion kuvaaja on koordinaatistossa origon kautta kulkeva nouseva suora. Suoran yhtälö on muotoa \(y=kx\), missä \(k\) on suoran kulmakerroin.
Suoraan verrannollinen funktio
Kuvaajan yhtälö:
\(y=kx\).
Kulmakerroin:
\(\displaystyle{k=\frac{y}{x}}\).
Esimerkissä 1 kulmakerroin \(k=2\) on itse asiassa banaanien kilohinta 2 €/kg.
Esim. 2. Suoraan verrannollinen tehtävä.
Lettuihin tulee jauhoja 150 g ja nestettä 6 dl. Kuinka paljon tarvitaan nestettä, jos jauhoja tulee 500 g?
| jauhoja (g) | nestettä (dl) |
|---|---|
| 150 | 6 |
| 500 | x |
\( \begin{aligned} \frac{150\ \text{g}}{500\ \text{g}}&=\frac{6\ \text{dl}}{x} \quad\quad\quad||\ \text{kerrotaan ristiin}\ (x\neq0)\\ 150\cdot x&=500\cdot 6\ \text{dl} \quad\ ||:150\\ x&=\frac{500\cdot 6\ \text{dl}}{150}=20\ \text{dl} \end{aligned} \)
Vastaus: Nestettä tarvitaan \(20\ \text{dl}\).
7.2 Kääntäen verrannollisuus
Jos suureet A ja B ovat kääntäen verrannollisia, niin ne muuttuvat samassa suhteessa eri suuntiin. Esimerkiksi jos suure A kaksinkertaistuu, niin suure B pienenee puoleen.
Esim. 1. Nopeuden vaikutus matkaan kuluvaan aikaan.
Matkaan kuluva aika on kääntäen verrannollinen nopeuteen, jolla matka kuljetaan.
| nopeus (km/h) | aika (h) |
|---|---|
| 10 | 6 |
| 20 | 3 |
| 30 | 2 |
| 60 | 1 |
| 120 | 0,5 |
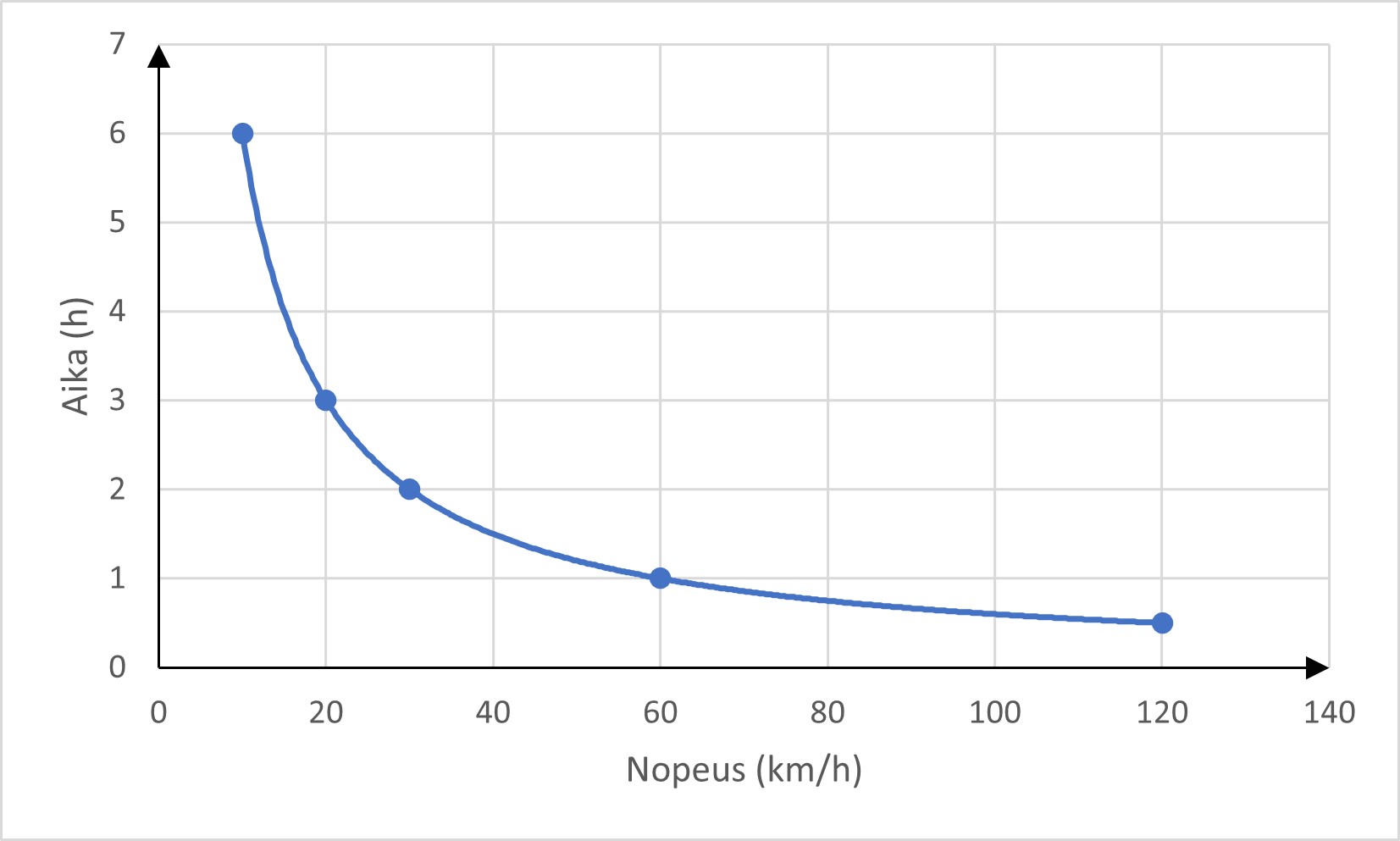
Kääntäen verrannollisen funktion kuvaaja on koordinaatistossa hyperbeli. Kuvaajan yhtälö on muotoa \(y=\frac{k}{x}\), missä \(k\) on verrannollisuuskerroin.
Kääntäen verrannollinen funktio
Kuvaajan (hyperbeli) yhtälö:
\(\displaystyle{y=\frac{k}{x}}\).
Verrannollisuuskerroin:
\(k=yx\).
Esimerkissä 1 verrannollisuuskerroin \(k=60\) on itse asiassa kuljettu välimatka 60 km.
Esim. 2 Kääntäen verrannollinen tehtävä.
Henkilöauton nopeus on 100 km/h ja pikajunan 180 km/h. Missä ajassa auto kulkee matkan, johon junalta kuluu 1,5 h?
| nopeus (km/h) | aika (h) |
|---|---|
| 100 | x |
| 180 | 1,5 |
\( \begin{aligned} \frac{100\ \text{km/h}}{180\ \text{km/h}}&=\frac{1{,}5\ \text{h}}{x} \quad\quad\ \ \ ||\ \text{kerrotaan ristiin}\ (x\neq0)\\ 100\cdot x&=180\cdot 1{,}5\ \text{h} \quad||:100\\ x&=\frac{180\cdot 1{,}5\ \text{h}}{100}=2{,}7\ \text{h} \end{aligned} \)
Muunnetaan tunnin kymmenesosat minuuteiksi \(0{,}7\cdot60\ \text{min}=42\ \text{min}\).
Vastaus: Auto kulkee matkan ajassa \(2\ \text{h}\ 42\ \text{min}\).