Geometria (MAA3)
Laajuus
2 op
Yleiset tavoitteet (LOPS 2021)
Moduulin tavoitteena on, että opiskelija
- harjaantuu hahmottamaan ja kuvaamaan tilaa ja muotoa koskevaa tietoa sekä kaksi- että kolmiulotteisissa tilanteissa
- osaa soveltaa yhdenmuotoisuutta, Pythagoraan lausetta sekä suora- ja vinokulmaisen kolmion trigonometriaa
- harjaantuu muotoilemaan, perustelemaan ja käyttämään geometrista tietoa sisältäviä lauseita
- osaa käyttää ohjelmistoja tutkiessaan kuvioita ja kappaleita sekä niihin liittyvää geometriaa
Keskeiset sisällöt (LOPS 2021)
- kuvioiden ja kappaleiden yhdenmuotoisuus
- sini- ja kosinilause
- monikulmioihin liittyvien pituuksien, kulmien ja pinta-alojen laskeminen
- ympyrän ja sen osien ja siihen liittyvien suorien geometria
- suoraan lieriöön ja suoraan kartioon sekä palloon liittyvien pituuksien, pinta-alojen ja tilavuuksien laskeminen
Aikataulu
Suoritus
- osallistuminen
- oppikirjan tehtävien tekeminen
- kaksi harjoitustehtävää
- loppukoe
Arviointi
- säännöllinen, aktiivinen ja vastuullinen osallistuminen +1 p
- enintään neljä poissaoloa
- tehtävien asianmukainen ja jatkuva tekeminen +3 p
- vähintään yksi asianmukaisesti tehty oppikirjan tehtävä käytössä ollutta oppituntia kohden
- tarkistetaan kahden viikon jaksoissa
- harjoitustehtävät 2 x 12 p = 24 p
- loppukoe 6 x 12 p = 72 p
- yhteensä max. 100 p
- 30 % arviointi
Arvosanataulukko
| Pisteet | Arvosana | Muuta |
|---|---|---|
| 0 - 14 | i \(\to\) K | Pakko täydentää. |
| 15 - 29 | 4 | Oikeus täydentää. |
| 30 - 42 | 5 | |
| 43 - 55 | 6 | |
| 56 - 68 | 7 | |
| 69 - 81 | 8 | |
| 82 - 94 | 9 | |
| 95 - 100 | 10 |
Keskeyttäminen
Opettaja keskeyttää opiskelijan opintojakson, jos
- opiskelija niin pyytää
- opiskelija ei ole läsnä opintojakson kahdella ensimmäisellä opetuskerralla ja opiskelija ei ole yhteydessä opettajaan eikä opettaja saa yhteyttä opiskelijaan.
Opettaja voi keskeyttää opiskelijan opintojakson, jos opiskelijalla on neljä poissaoloa. Tällaiset tilanteet opettaja käy läpi tapauskohtaisesti ja on ennen lopullista keskeytystä yhteydessä opiskelijaan.
Keskeyttämisestä opettaja merkitsee opintojaksosta opiskelijalle K-merkinnän Wilmaan ja poistaa opiskelijan sen jälkeen Wilman ryhmästä. Opettaja lähettää keskeyttämisestä viestin opiskelijalle, alaikäisen opiskelijan huoltajalle, ryhmänohjaajalle ja opolle.
1 TASOGEOMETRIAN PERUSTEITA
1.1 Peruskäsitteitä
Piste ja viiva
Piste on geometrian perustavanlaatuisimpia käsitteitä. Alkeiskäsitteenä sille ei ole määritelmää. Voitaneen sanoa, että piste on avaruuden äärettömän pieni kohta. Pisteellä ei ole mittaa.
Viiva on pisteiden ura.
Erilaisia viivoja
- suora = äärettömän pitkä suora viiva
- puolisuora = suora viiva, jolla on yksi päätepiste
- jana = suora viiva, jolla on kaksi päätepistettä
- murtoviiva = muodostuu peräkkäin olevista janoista
Viiva voi olla
- suljettu = päätepisteet kohtaavat
- avoin = päätepisteet eivät kohtaa
- itseään leikkaava
- itseään leikkaamaton
Kulma
Kulma on kahden samasta pisteestä alkavan puolisuoran väliin jäävä aukeama.
Kulma voidaan nimetä oikean kyljen pisteen, kärkipisteen ja vasemman kyljen pisteen mukaan tai pelkän kärkipisteen mukaan taikka kreikkalaisilla kirjaimilla.
Kulmien luokittelua
- nollakulma, \(0^{\circ}\)
- suorakulma, \(90^{\circ}\)
- oikokulma, \(180^{\circ}\)
- täysi kulma, \(360^{\circ}\)
- terävä kulma, \(0^{\circ}<\alpha<90^{\circ}\)
- tylppä kulma, \(90^{\circ}<\alpha<180^{\circ}\)
- kovera kulma, \(0^{\circ}<\alpha<180^{\circ}\)
- kupera kulma, \(180^{\circ}<\alpha<360^{\circ}\)
1.2 Leikkaavat suorat
Tasossa kulkevat suorat ovat yhdensuuntaiset, jos niillä ei ole yhtään yhteistä pistettä, tai ne yhtyvät.
Jos suorat eivät ole yhdensuuntaiset, ne leikkaavat toisensa yhdessä pisteessä.
Suorat, jotka ovat kohtisuorassa eli \(90^{\circ}\):een kulmassa toisiinsa nähden, ovat toistensa normaaleja.
Vieruskulmat ja ristikulmat
Kun kaksi suoraa leikkaa, syntyy yhteensä neljä kulmaa. Kaksi vierekkäistä kulmaa ovat toistensa vieruskulmia. Toisiaan vastapäätä olevat kulmat ovat toistensa ristikulmia.
Vieruskulmien summa on \(180^{\circ}\).
Ristikulmat ovat yhtä suuret.
Samankohtaiset kulmat
Kun suora leikkaa kahta muuta suoraa, syntyy yhteensä kahdeksan kulmaa. Ensimmäisessä leikkauskohdassa olevalle kulmalle ovat samankohtaisia kulmia ne toisen leikkauskohdan kulmat, joilla leikkaava suora on samana kulman kylkenä kuin ensimmäisen leikkauskohdan kulmalla.
Yhdensuuntaisuuslause
Kolmannen suoran leikkaamat kaksi suoraa ovat yhdensuuntaiset, jos näin syntyvät samankohtaiset kulmat ovat yhtä suuret.
Lause on yhtäpitävä eli pätee molempiin suuntiin.
1.3 Monikulmioita
Monikulmio on suljetun, itseään leikkaamattoman murtoviivan rajaama tasoalue.
Säännöllisen monikulmion kaikki sivut ovat yhtä pitkiä ja kaikki kulmat yhtä suuria.
Erilaisia kolmioita
- teräväkulmainen kolmio = kaikki kulmat ovat teräviä
- tylppäkulmainen kolmio = yksi kulma on tylppä
- suorakulmainen kolmio = yksi kulma on suora
- tasakylkinen kolmio = kaksi sivua (kolmion kyljet) ovat yhtä pitkät ja kaksi kulmaa (kanta kulmat) ovat yhtä suuret
- tasasivuinen kolmio (eli säännöllinen kolmio) = kaikki sivut ovat yhtä pitkiä ja kaikki kulmat yhtä suuria
Erilaisia nelikulmioita
- puolisuunnikas = kaksi yhdensuuntaista sivua
- suunnikas = vastakkaiset sivut yhdensuuntaiset ja yhtä pitkät
- neljäkäs eli vinoneliö = vastakkaiset sivut yhdensuuntaiset ja kaikki sivut yhtä pitkiä
- suorakulmio = vastakkaiset sivut yhtä pitkiä ja kaikki kulmat suoria
- neliö (eli säännöllinen nelikulmio) = kaikki sivut yhtä pitkiä ja kaikki kulmat suoria
Monikulmion kulmien summa
Monikulmion kulmien summa voidaan laskea lausekkeella \( \left(n-2\right)\cdot 180^{\circ} \), missä \(n\) on monikulmion kulmien lukumäärä.
Erityisesti kolmion kulmien summa on \(180^{\circ}\).
Monikulmion piiri
Monikulmion piiri tarkoittaa tasokuvion reunan pituutta eli ympärysmittaa. Monikulmion piiri lasketaan monikulmion sivujen pituuksien summana.
Monikulmioiden pinta-aloja
Monikulmion pinta-ala tarkoittaa tasokuvion peittämän alueen kokoa.
Suorakulmion pinta-ala, \(A\), lasketaan kanta, \(a\), kertaa korkeus, \(h\).
$$A=ah$$
Neliö on suorakulmio, jonka on kaikki sivut ovat yhtä pitkiä. Neliön pinta-ala, \(A\), on siis sivun pituuden, \(a\), neliö.
$$A=a^2$$
Suunnikas voidaan palauttaa suorakulmioksi. Suunnikkaan pinta-ala lasketaan siis kuten suorakulmion pinta-ala eli kanta kertaa korkeus.
Puolisuunnikkaan pinta-ala, \(A\), voidaan laskea siten, että yhdensuuntaisten sivujen, \(a\) ja \(b\), pituuksien keskiarvo kerrotaan puolisuunnikkaan korkeudella, \(h\).
$$A=\frac{a+b}{2}\cdot h$$
Kolmion pinta-ala, \(A\), lasketaan kanta, \(a\), kertaa korkeus, \(h\), jaettuna kahdella.
$$A=\frac{ah}{2}$$
Kolmion pinta-ala on siis puolet suunnikkaasta, jonka kanta ja korkeus ovat samat kuin kolmiolla.
Monimutkaisempien monikulmioiden pinta-aloja voidaan laskea esimerkiksi jakamalla tasokuvio osiin, joiden pinta-alat on mahdollista laskea yllä esitettyjen kaavojen avulla.
2 YHDENMUOTOISUUS
2.1 Mittakaava
Yhdenmuotoisuus
Kaksi kuviota ovat yhdenmuotoiset, jos niillä on sama muoto.
Yhdenmuotoisuuskuvaukset siirto, kierto, peilaus ja skaalaus säilyttävät yhdenmuotoisuuden.
Yhdenmuotoisissa kuvioissa
- vastinkulmat ovat yhtä suuret,
- vastinosien pituuksien suhteet ovat yhtä suuret.
Mittakaava
Mittakaava, \(k\), on vastinosien pituuksien suhde.
Suhde on jakolasku. Mittakaava voidaan esittää jakolaskuna jakoviivalla tai jakopisteellä merkittynä \(k=\frac{a}{b}=a:b\).
Huom.
Vakiintunut tapa on, että mittakaavalla ilmaistaan kuvan suhde alkuperäiseen kuvioon. Jos ei ole pääteltävissä, kumpi on kuva ja kumpi alkuperäinen kuvio, voi järjestyksen määrittää itse.
Yhtenevyys
Kaksi kuviota ovat yhtenevät, jos ne ovat yhdenmuotoiset ja samankokoiset.
Huom.
Yhtenevien kuvioiden mittakaava on \(k=1:1\).
Esim. 1
Kolmiot \(ABC\) ja \(DEF\) ovat yhdenmuotoiset \(\left(\Delta ABC \sim \Delta DEF\right)\).
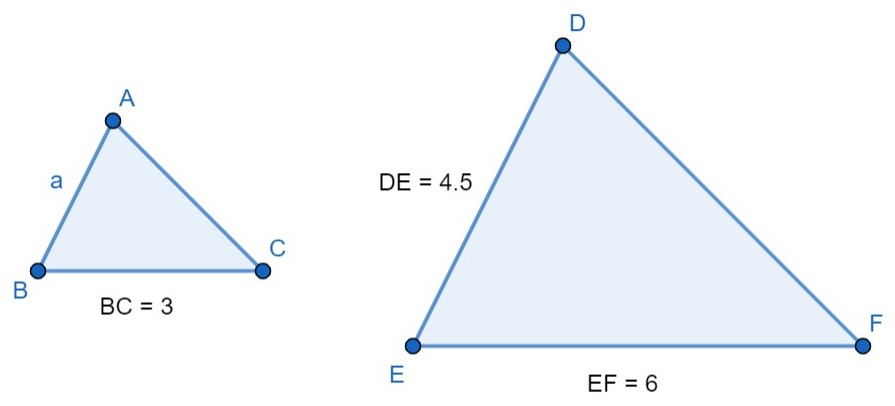
a) Taulukoi vastinosat.
b) Määritä kolmioiden mittakaava.
c) Laske sivun \(a\) pituus.
a) Taulukoidaan vastinsivut:
| \(\Delta ABC\) | \(\Delta DEF\) |
|---|---|
| \(AB\) | \(DE\) |
| \(BC\) | \(EF\) |
| \(AC\) | \(DF\) |
b) Monikulmioiden mittakaava saadaan vastinsivujen pituuksien suhteena. Valitaan yksi pari vastinsivuja ja määritetään niiden suhde.
\(3:6=\frac{3}{6}^{(3}=\frac{1}{2}=1:2\)
Vastaus: Mittakaava on \(1:2\).
c) Tapa 1:
Mittakaava ilmaisee, että kolmion \(ABC\) sivujen pituudet ovat puolet kolmion \(DEF\) sivujen pituuksista.
$$a=\frac{1}{2}\cdot 4{,}5\ \text{cm}=2{,}25\ \text{cm}\approx2{,}3\ \text{cm}$$
Tapa 2:
Koska vastinsivujen suhteet ovat samat, voidaan hyödyntää verrantoa.
| \(\Delta ABC\) | \(\Delta DEF\) |
|---|---|
| \(a\) | \(4{,}5\ \text{cm}\) |
| \(3\ \text{cm}\) | \(6\ \text{cm}\) |
$$ \begin{align} \frac{a}{3\ \text{cm}}&=\frac{4{,}5\ \cancel{\text{cm}}}{6\ \cancel{\text{cm}}}\\ 6a&=4{,}5 \cdot 3\ \text{cm}\\ a&=\frac{4{,}5 \cdot 3\ \text{cm}}{6}=2{,}25\ \text{cm}\approx2{,}3\ \text{cm} \end{align} $$
Vastaus: Sivun \(a\) pituus on noin \(2{,}3\ \text{cm}\).
Kolmioiden yhdenmuotoisuus voidaan todeta, jos tiedetään vähintään kahden vastinkulman suuruus.
Kolmioiden yhdenmuotoisuuslause (kk-lause)
Jos kolmion kahdella kulmalla on yhtä suuri vastinkulma toisessa kolmiossa, ovat kolmiot yhdenmuotoiset.
Esim. 2
Iltapäivällä maahan pystyyn laitetun 70 cm pitkän kepin varjo oli 1,2 m. Puun varjo oli 15 m. Mikä oli puun korkeus?
Piirretään mallikuva. Merkitään puun korkeus \(x\).
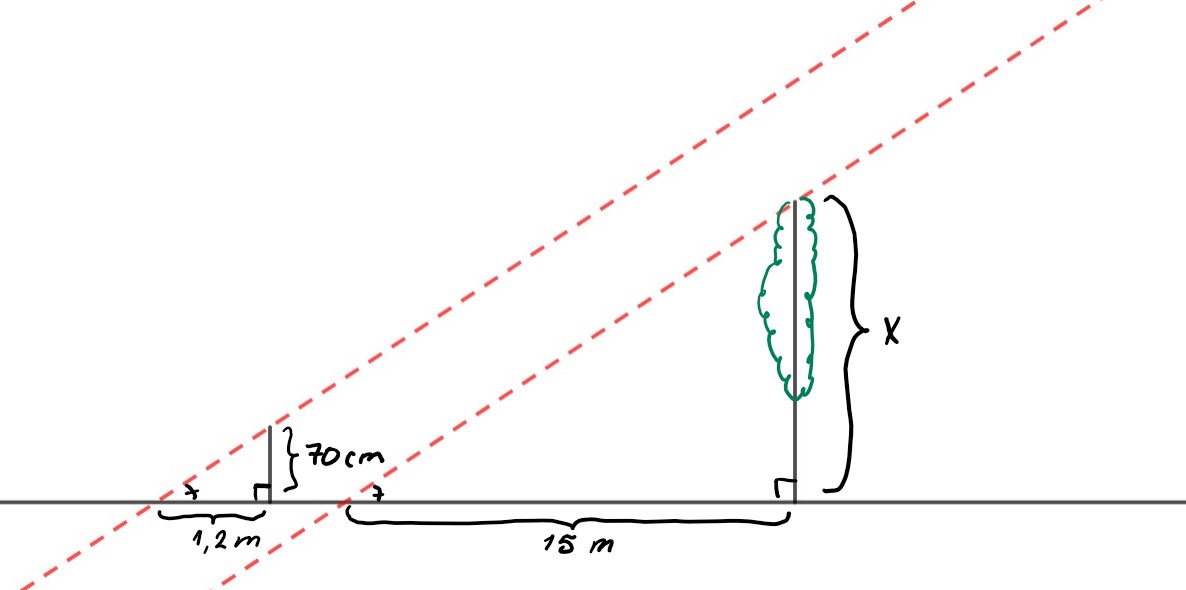
Puun ja kepin oletetaan olevan kohtisuorassa maata vastaan (suorakulma).
Kaukaisesta pistemäisestä kohteesta saapuvien valonsäteiden oletaan kulkevan yhdensuuntaisina. Siten puun ja kepin ylittävien valonsäteiden ja maan väliset kulmat ovat samankohtaisina kulmina yhtä suuret.
Koska kuvan suorakulmaisissa kolmioissa on kaksi yhtä suurta kulmaa, ovat kolmiot kk-lauseen perusteella yhdenmuotoiset.
Yhdenmuotoisissa kolmioissa vastinsivujen suhteet ovat yhtä suuret.
Muutetaan \(70\ \text{cm}=0{,}7\ \text{m}\).
Kirjoitetaan verrantoyhtälö.
$$ \begin{align} \frac{x}{15\ \text{m}}&=\frac{0{,}7\ \cancel{\text{m}}}{1{,}2\ \cancel{\text{m}}}\\ 1{,}2x&=0{,}7 \cdot 15\ \text{m}\\ x&=\frac{0{,}7 \cdot 15\ \text{m}}{1{,}2}=8{,}75\ \text{m}\approx8{,}8\ \text{m} \end{align} $$
Vastaus: Puun korkeus on noin \(8{,}8\ \text{m}\).
2.2 Pinta-alojen ja tilavuuksien suhde
Tutkimus
Piirretään suunnikas, jonka kanta on \(a\) ja korkeus \(h\). Piirretään suunnikkaasta kuva mittakaavassa \(3:1\). Määritetään suunnikkaiden pinta-alat. Määritetään kuvan ja alkuperäisen suunnikkaan pinta-alojen suhde. Mitä havaitaan?
Pinta-alojen suhde
Pinta-alojen suhde on mittakaavan neliö.
Esim. 1
Kolmiot ovat yhdenmuotoiset mittakaavassa \(3:2\). Laske suuremman kolmion pinta-ala, kun pienemmän kolmion pinta-ala on \(12\ \text{m}^2\).
\(k=3:2\)
\(k^{2}=(3:2)^{2}=\left(\frac{3}{2}\right)^{2}=\frac{9}{4}\)
Suuremman kolmion pinta-ala:
$$\frac{9}{4}\cdot12\ \text{m}^2=\frac{108\ \text{m}^2}{4}=27\ \text{m}^2 $$
Vastaus: \(27\ \text{m}^2\)
Tilavuuksien suhde
Tilavuuksien suhde on mittakaavan kuutio.
3 KOLMIO
3.1 Suorakulmainen kolmio
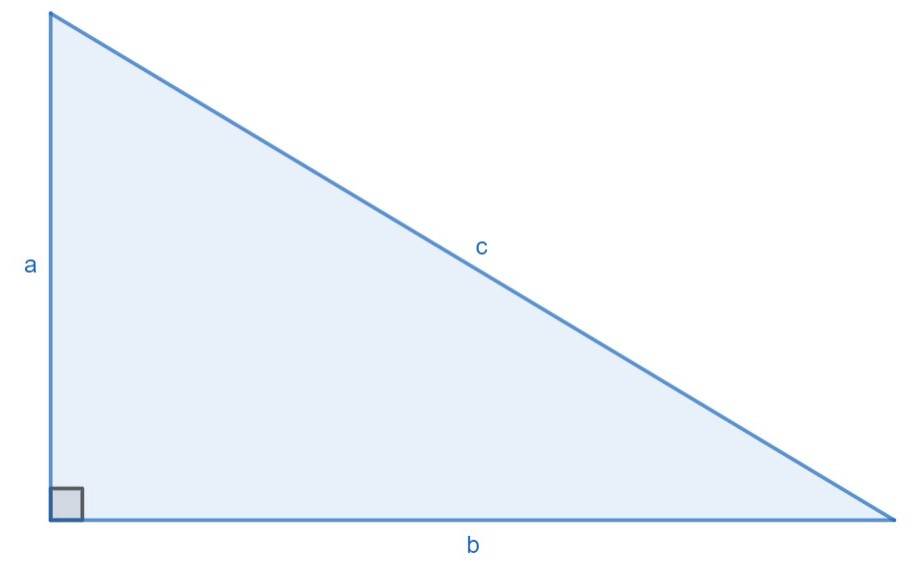
Suorakulmaisessa kolmiossa lyhyempiä sivuja \(a\) ja \(b\) kutsutaan kateeteiksi ja pisintä sivua \(c\) hypotenuusaksi.
Pythagoraan lause
Suorakulmaisessa kolmiossa kateettien \(a\) ja \(b\) pituuksien neliöiden summa on hypotenuusan \(c\) pituuden neliö.
$$a^{2}+b^{2}=c^{2}$$
Esim. 1
Kolmion kaksi lyhyempää sivua ovat \(4\ \text{cm}\) ja \(7\ \text{cm}\) ja pisin sivu \(8\ \text{cm}\).
a) Onko kolmio suorakulmainen?
b) Jos kolmio ei ole suorakulmainen, onko lyhyempien sivujen välinen kulma yli vai alle \(90^{\circ}\)?
a) Tutkitaan kolmion suorakulmaisuus Pythagoraan lauseen avulla.
$$\begin{align} 4^{2}+7^{2}&=8^{2} \\ 16+49&=64 \\ 65&=64\ \text{(epätosi)} \end{align}$$
Vastaus: Kolmio ei ole suorakulmainen.
b) A-kohdan perusteella \(65>64\) eli Pythagoraan lauseen hypotenuusan pituuden neliötä vastaava lukuarvo on pienempi ja näin ollen lyhyempien sivujen välinen kulma on alle \(90^{\circ}\).
Vastaus: Lyhyempien sivujen välinen kulma on alle \(90^{\circ}\).
Esim. 2
Suorakulmaisen kolmion hypotenuusa on \(10{,}0\ \text{cm}\) ja lyhyempi kateetti \(5{,}0\ \text{cm}\). Laske kolmion pinta-ala.
Lasketaan Pythagoraan lauseen avulla pidemmän kateetin pituus.
$$\begin{eqnarray} 5{,}0^{2}+x^{2}&=&10{,}0^{2}&\quad ||&-5{,}0^{2} \\ x^{2}&=&10{,}0^{2}-5{,}0^{2}&& \\ x^{2}&=&100{,}0-25{,}0&& \\ x^{2}&=&75{,}0&\quad ||&\sqrt{} \\ x&=&\pm \sqrt{75{,}0}&& \end{eqnarray}$$
Kateetin pituus on lukuarvoltaan aina positiivinen, joten negatiivinen arvo voidaan hylätä.
Lasketaan kolmion pinta-ala.
$$A=\frac{5{,}0\cdot \sqrt{75{,}0}}{2} \approx21{,}6506\approx 21{,}7$$
Vastaus: Kolmion pinta-ala on \(21{,}7\ \text{cm}^{2}\).
Trigonometriset funktiot
$$\sin \alpha=\frac{\text{kulman}\ \alpha\ \text{vastainen kateetti}}{\text{hypotenuusa}}$$
$$\cos \alpha=\frac{\text{kulman}\ \alpha\ \text{viereinen kateetti}}{\text{hypotenuusa}}$$
$$\tan \alpha=\frac{\text{kulman}\ \alpha\ \text{vastainen kateetti}}{\text{kulman}\ \alpha\ \text{viereinen kateetti}}$$
Trigonometristen funktioiden avulla voidaan laskea suorakulmaisen kolmion sivun pituus, kun tunnetaan yksi kulma ja yksi sivu, tai kulman suuruus, kun tunnetaan kahden sivun pituudet.
Esim. 3
Laske sivun \(x\) pituus.
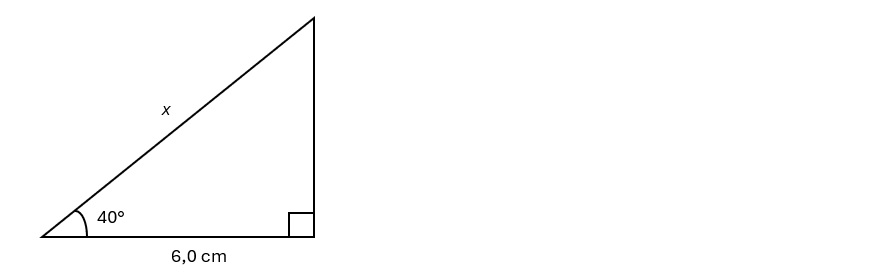
Tunnistetaan sopiva trigonometrinen funktio, kirjoitetaan yhtälö ja ratkaistaan se.
\(\begin{align} \cos40^{\circ}&=\frac{6{,}0\ \text{cm}}{x}\quad\mid \cdot\, x \\ \\ x\cos40^{\circ}&=6{,}0\ \text{cm}\quad\ \, \mid\, :\cos40^{\circ} \\ \\ x&=\frac{6{,}0\ \text{cm}}{\cos40^{\circ}}\\ \\ &=7{,}832\ldots\ \text{cm}\\ \\ &\approx7{,}8\ \text{cm} \end{align}\)
Vastaus: \(7{,}8\ \text{cm}\).
Esim. 4
Laske kulman \(\alpha\) suuruus.
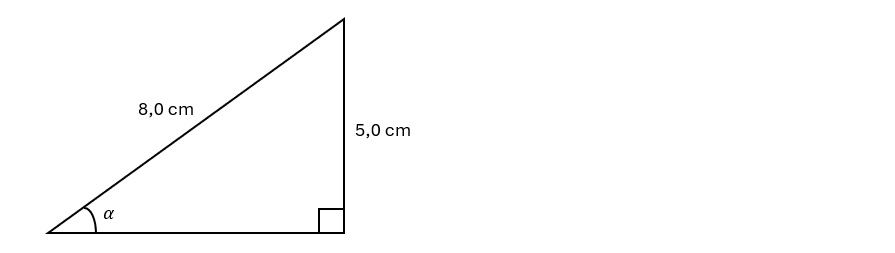
Tunnistetaan sopiva trigonometrinen funktio, kirjoitetaan yhtälö ja ratkaistaan se.
\(\begin{align} \sin\alpha&=\frac{5{,}0\ \text{cm}}{8{,}0\ \text{cm}}\quad\mid\arcsin \\ \\ \alpha&=38{,}682\ldots^{\circ} \\ \\ &\approx38{,}7^{\circ} \end{align}\)
Vastaus: \(38{,}7^{\circ}\).
3.2 Sinilause
Kolmion pinta-ala
$$ A=\frac{1}{2}ab\sin\beta, $$
missä kulma \(\beta\) on sivujen \(a\) ja \(b\) välinen kulma.
Esim. 1
Kolmion kahden sivun pituudet ovat 4 ja 5 ja pinta-ala on 9. Määritä sivujen välisen kulman suuruus
a) GeoGebralla piirtämällä
b) laskemalla.
b) Muodostetaan yhtälö kolmion pinta-alan lausekkeesta ja ratkaistaan.
\(\begin{align} A&=\frac{1}{2}ab\sin\alpha\\ \\ 9&=\frac{1}{2}\cdot4\cdot5\sin\alpha\\ \\ \sin\alpha&=\frac{9}{\frac{1}{2}\cdot4\cdot5}\\ \\ \alpha&\approx65^{\circ}\quad\text{tai}\quad\alpha\approx180^{\circ}-65^{\circ}=115^{\circ} \end{align}\)
Vastaus: \(\alpha\approx65^{\circ}\quad\text{tai}\quad\alpha\approx115^{\circ}\).
Huom.
Kun kulman \(\alpha\) suuruutta ratkaistaan GeoGebran CAS-laskimen Ratkaise-komennolla, on ratkaisut rajattava välille \(0^{\circ}\lt\alpha\lt180^{\circ}\).
Sinin ominaisuuksia
1) Suplementtikulmien sinit ovat yhtä suuret: \(\sin\beta=\sin\left(180^{\circ}-\beta\right)\).
2) Suoran kulman sini on aina 1: \(\sin90^{\circ}=1\).
Sinilause
Kolmiossa sivun pituuden ja sivua vastapäätä olevan kulman sinin suhde on vakio.
$$ \frac{a}{\sin\alpha}=\frac{b}{\sin\beta}=\frac{c}{\sin\gamma} $$
Esim. 2
Kolmion lyhimmän sivun pituus on \(7{,}5\ \text{cm}\). Kolmion kaksi kulmaa ovat \(26^{\circ}\) ja \(78^{\circ}\). Laske kolmion pisimmän sivun pituus.
Lasketaan kolmannen kulman suuruus ja hahmotellaan mallikolmio.
\(180^{\circ}-(26^{\circ}+78^{\circ})\)
\(=180^{\circ}-104^{\circ}\)
\(=76^{\circ}\)
On siis laskettava \(78^{\circ}\):een kulmaa vastapäätä sijaitsevan sivun pituus.
Sinilause:
\(\begin{align} \frac{x}{\sin78^{\circ}}&=\frac{7{,}5\ \text{cm}}{\sin26^{\circ}}\\ \\ x\cdot\sin26^{\circ}&=7{,}5\ \text{cm}\cdot\sin78^{\circ} \quad \mid\, :\sin26^{\circ}\\ \\ x&=\frac{7{,}5\ \text{cm}\cdot\sin78^{\circ}}{\sin26^{\circ}}\\ \\ &=16{,}734\ldots\ \text{cm}\\ \\ &\approx16{,}7\ \text{cm} \end{align}\)
Vastaus: \(16{,}7\ \text{cm}\).
Esim. 3
Kolmion yksi kulma on \(32^{\circ}\). Kulman vieressä vasemmalla oleva kolmion sivu on \(4{,}7\ \text{cm}\) ja vastapäinen sivu \(3{,}6\ \text{cm}\). Laske kolmion kahden muun kulman suuruudet.
Hahmotellaan mallikolmio. Havaitaan, että annettuja tietoja vastaa kaksi mahdollista kolmiota. Merkitään kulmia \(\alpha\) ja \(\alpha'\) sekä \(\beta\) ja \(\beta'\).
Ratkaistaan sinilauseen avulla \(\alpha\) ja \(\alpha'\):
\(\begin{align} \frac{4{,}7\ \text{cm}}{\sin\alpha}&=\frac{3{,}6\ \text{cm}}{\sin32^{\circ}}\\ \\ 3{,}6\ \text{cm}\cdot\sin\alpha&=4{,}7\ \text{cm}\cdot\sin32^{\circ} \quad \mid\, :3{,}6\ \text{cm}\\ \\ \sin\alpha&=\frac{4{,}7\ \text{cm}\cdot\sin32^{\circ}}{3{,}6\ \text{cm}}\ \ \mid\arcsin\\ \\ \alpha&=43{,}775\ldots^{\circ}\\ \\ &\approx44^{\circ} \end{align}\)
tai suplementtikulma
\(\alpha'=180^{\circ}-44^{\circ}=136^{\circ}.\)
Lasketaan kolmannen kulman suuruus:
\(\begin{align} \beta&=180^{\circ}-(32^{\circ}+44^{\circ})\\ \\ &=180^{\circ}-76^{\circ}\\ \\ &=104^{\circ} \end{align}\)
tai
\(\begin{align} \beta'&=180^{\circ}-(32^{\circ}+136^{\circ})\\ \\ &=180^{\circ}-168^{\circ}\\ \\ &=12^{\circ}. \end{align}\)
Vastaus: Kaksi muuta kulmaa ovat \(44^{\circ}\) ja \(104^{\circ}\) tai \(136^{\circ}\) ja \(12^{\circ}\).
3.3 Kosinilause
Kosinilause
$$c^{2}=a^{2}+b^{2}-2ab\cos\gamma,$$
missä kulma \(\gamma\) on sivua \(c\) vastapäätä.
Kosinin ominaisuuksia
Suoran kulman kosini on nolla: \(\cos90^{\circ}=0\).
Huom.
Kun kulma \(\gamma=90^{\circ}\) kosinilause palautuu Pythagoraan lauseeksi.
Esim. 1
Kolmion sivujen pituudet ovat \(4{,}0\ \text{cm}\), \(5{,}0\ \text{cm}\) ja \(6{,}0\ \text{cm}\). Laske kolmion pienimmän kulman suuruus.
Pienin kulma on lyhintä sivua vastapäätä.
\(\begin{align} c^{2}&=a^{2}+b^{2}-2ab\cos\gamma\\ \\ 4{,}0^{2}&=5{,}0^{2}+6{,}0^{2}-2\cdot5{,}0\cdot6{,}0\cos\gamma\\ \\ 2\cdot5{,}0\cdot6{,}0\cos\gamma&=5{,}0^{2}+6{,}0^{2}-4{,}0^{2}\\ \\ \cos\gamma&=\frac{5{,}0^{2}+6{,}0^{2}-4{,}0^{2}}{2\cdot5{,}0\cdot6{,}0}\\ \\ \gamma&=41{,}409\ldots^{\circ}\approx41{,}4^{\circ} \end{align}\)
Vastaus: \(41{,}4^{\circ}\).
Esim. 2
Laske kolmion kolmannen sivun pituus, kun kolmion kahden sivun pituudet ovat
a) \(4{,}0\ \text{cm}\) ja \(6{,}0\ \text{cm}\) ja sivujen välinen kulma on \(27^{\circ}\)
b) \(4{,}0\ \text{cm}\) ja \(6{,}0\ \text{cm}\) ja jälkimmäisen vastainen kulma on \(27^{\circ}\)
c) \(6{,}0\ \text{cm}\) ja \(4{,}0\ \text{cm}\) ja jälkimmäisen vastainen kulma on \(27^{\circ}\).
a) Voidaan ratkaista käsin tai CAS-laskimella.
\(\begin{align} c^{2}&=a^{2}+b^{2}-2ab\cos\gamma\\ \\ c^{2}&=4{,}0^{2}+6{,}0^{2}-2\cdot4{,}0\cdot6{,}0\cos27^{\circ}\\ \\ c&=\pm\sqrt{4{,}0^{2}+6{,}0^{2}-2\cdot4{,}0\cdot6{,}0\cos27^{\circ}}\\ \\ c&=\pm3{,}038\ldots\approx\pm3{,}0 \end{align}\)
Pituus on positiivista.
Vastaus: \(3{,}0\ \text{cm}\).
b) Voidaan ratkaista vain CAS-laskimella ennen MAA2:a.
\(\begin{align} c^{2}&=a^{2}+b^{2}-2ab\cos\gamma\\ \\ 6{,}0^{2}&=4{,}0^{2}+b^{2}-2\cdot4{,}0b\cos27^{\circ}\quad\mid\,\text{CAS-laskin}\\ \\ b&=-2{,}154\ldots\quad\text{tai}\quad b=9{,}282\ldots \end{align}\)
Pituus on positiivista.
Vastaus: \(9{,}3\ \text{cm}\).
c) Voidaan ratkaista vain CAS-laskimella ennen MAA2:a.
\(\begin{align} c^{2}&=a^{2}+b^{2}-2ab\cos\gamma\\ \\ 4{,}0^{2}&=6{,}0^{2}+b^{2}-2\cdot6{,}0b\cos27^{\circ}\quad\mid\,\text{CAS-laskin}\\ \\ b&=2{,}416\ldots\quad\text{tai}\quad b=8{,}275\ldots \end{align}\)
Vastaus: \(2{,}4\ \text{cm}\) tai \(8{,}3\ \text{cm}\).
4 YMPYRÄ
4.1 Ympyrään liittyviä käsitteitä
Ympyrä on niiden tason pisteiden joukko, jotka sijaitsevat säteen etäisyydellä keskipisteestä.
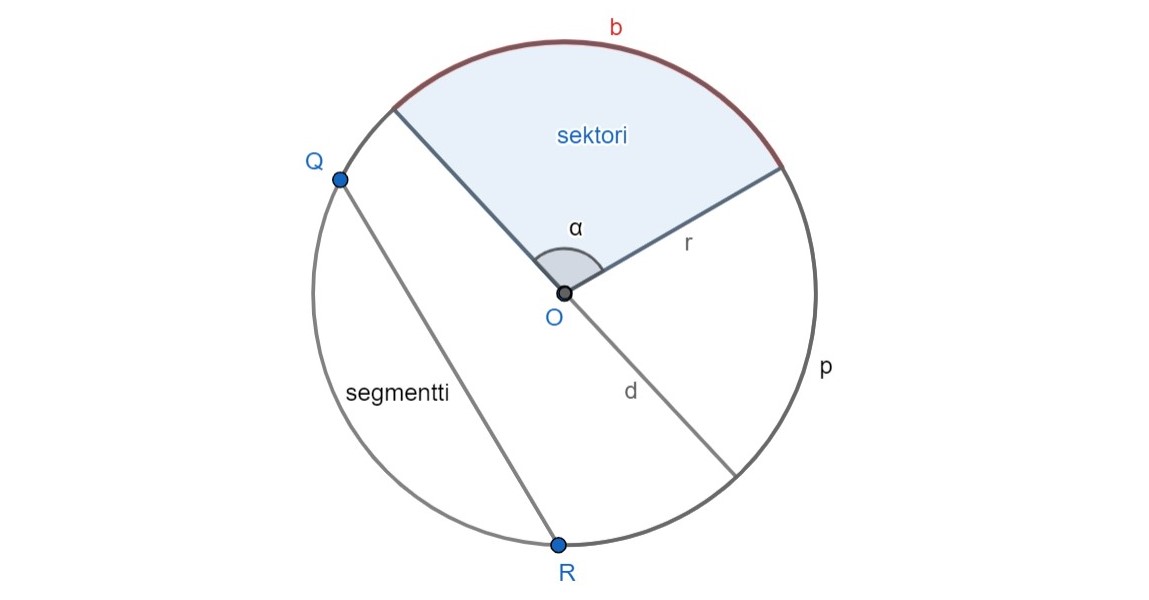
- keskipiste, \(O\)
- säde, \(r=\frac{d}{2}\)
- kehä, \(p\)
- halkaisija, \(d=2r\)
- keskuskulma, \(\alpha\)
- sektori
- kaari, \(b\)
- jänne, \(QR\)
- segmentti
4.2 Ympyrään liittyviä kaavoja
Piiri eli kehän pituus
Tässä applettissa havainnollistetaan piirin ja halkaisijan välistä suhdetta.
Ympyrän pinta-ala
Kaaren pituus
Sektorin pinta-ala
Esim. 1 (Segmentin pinta-alan laskeminen.)
Laske \(10^{\circ}\):een kaarta vastaavan segmentin pinta-ala, kun ympyrän piiri on \(20{,}0\ \text{cm}\).
Segmentin pinta-ala on \(A_{\text{segmentti}}=A_{\text{sektori}}-A_{\text{kolmio}}\).
Lasketaan ensin ympyrän säde.
$$ \begin{aligned} p&=2\pi r\\ 20,0\ \text{cm}&=2\pi r\\ r&=\frac{20{,}0\ \text{cm}}{2\pi}=\frac{10{,}0}{\pi}\ \text{cm}\\ \end{aligned} $$
Lasketaan sitten sektorin pinta-ala.
$$ \begin{aligned} A_{\text{sektori}}&=\frac{\alpha}{360^{\circ}}\cdot \pi r^{2}\\ &=\frac{10^{\circ}}{360^{\circ}}\cdot \pi \cdot \left(\frac{10{,}0}{\pi}\ \text{cm}\right)^{2}=\frac{25}{9\pi}\ \text{cm}^{2}\\ \end{aligned} $$
Lasketaan seuraavaksi pinta-ala sellaiselle tasakylkiselle kolmiolle, jonka kyljet ovat säteen mittaisia ja kylkien välinen kulma on \(10^{\circ}\).
$$ \begin{aligned} A_{\text{kolmio}}&=\frac{1}{2}ab\sin\beta\\ &=\frac{1}{2}\cdot \left(\frac{10{,}0}{\pi}\ \text{cm}\right)^{2}\cdot\sin10^{\circ}=\frac{50\sin10^{\circ}}{\pi^{2}}\ \text{cm}^{2}\\ \end{aligned} $$
Lasketaan lopuksi segmentin pinta-ala vähentämällä sektorin pinta-alasta kolmion pinta-ala.
$$ \begin{aligned} A_{\text{segmentti}}&=A_{\text{sektori}}-A_{\text{kolmio}}\\ &=\frac{25}{9\pi}\ \text{cm}^{2}- \frac{50\sin10^{\circ}}{\pi^{2}}\ \text{cm}^{2}\\ &=0{,}004482\ \text{cm}^{2}\approx0{,}4\ \text{mm}^{2}\\ \end{aligned} $$
Vastaus: Segmentin pinta-ala on noin \(0{,}4\ \text{mm}^{2}\).
4.3 Ympyrään liittyviä lauseita
ApplettiKehäkulman kärki on ympyrän kehällä. Sen toisen kyljen osana on jänne ja toisen kyljen osana jänne tai toisena kylkenä on tangentti.
Kehäkulmalause
Lause
Thaleen lause
Suoraa, joka sivuaa ympyrää yhdessä pisteessä, kutsutaan tangentiksi.
Lause
Tangenttikulma on kahden samalle ympyrälle piirretyn tangentin väliin jäävä kulma.
Lause
Suoraa, joka leikkaa ympyrän kahdessa pisteessä, kutsutaan sekantiksi.
Kolmio ja ympyrä
Kolmion sisään piirretty ympyrä
Kolmion kulmanpuolittajien leikkauspiste on kolmion sisään piirretyn ympyrän keskipiste.
Kolmion ympäri piirretty ympyrä
Kolmion sivujen keskinormaalien leikkauspiste on kolmion ympäri piirretyn ympyrän keskipiste.
5 AVARUUSGEOMETRIA
5.1 Suorakulmainen särmiö
Suorakulmainen särmiö on avaruuskappale, jonka osat ovat suorakulmioita. Kuutio on suorakulmaisen särmiön erityistapaus. Kuutio koostuu kuudesta neliöstä ja sen särmät ovat yhtä pitkät.
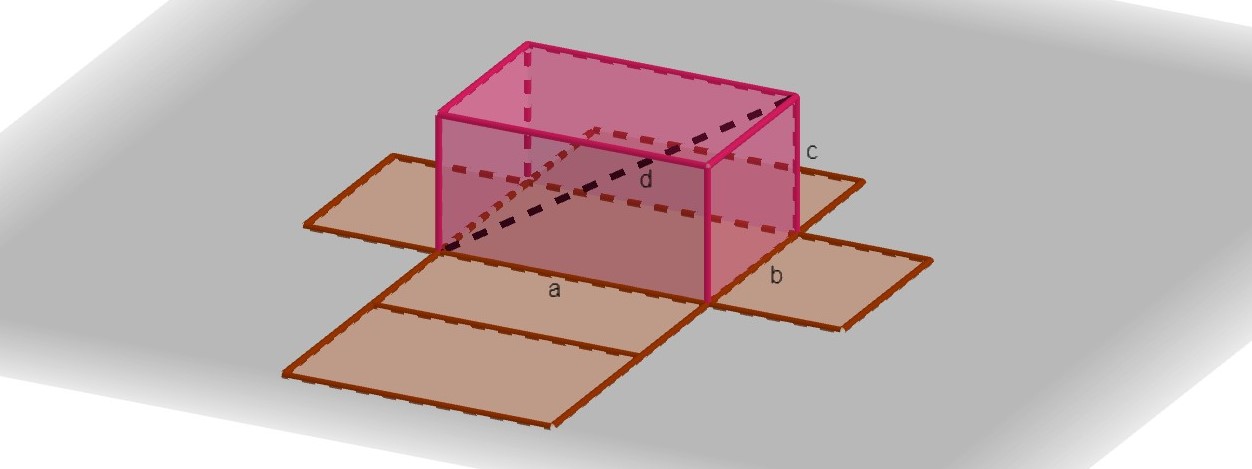
Suorakulmaisen särmiön tilavuus
$$V_{\text{SUORAK. SÄRMIÖ}}=abc,$$
missä \(a\), \(b\) ja \(c\) ovat suorakulmaisen särmiön leveys, syvyys ja korkeus.
Suorakulmaisen särmiön pinta-ala
$$A_{\text{SUORAK. SÄRMIÖ}}=2ab+2bc+2ac,$$
missä \(a\), \(b\) ja \(c\) ovat suorakulmaisen särmiön leveys, syvyys ja korkeus.
Pythagoraan lause kolmessa ulottuvuudessa
$$d^{2}=a^{2}+b^{2}+c^{2},$$
missä \(d\) vastaa suorakulmaisen särmiön avaruuslävistäjän pituutta ja \(a\), \(b\) ja \(c\) ovat suorakulmaisen särmiön leveys, syvyys ja korkeus.
Esim. 1
Suorakulmaisen särmiön mitat ovat leveys \(6\ \text{cm}\), syvyys \(4\ \text{cm}\) ja korkeus \(3\ \text{cm}\). Laske suorakulmaisen särmiön
a) tilavuus
b) pinta-ala
c) pohjan lävistäjä
d) avaruuslävistäjä.
a) Tilavuus:
\(\begin{align} V_{\text{SUORAK. SÄRMIÖ}}&=abc\\ \\ &=6\ \text{cm}\cdot4\ \text{cm}\cdot3\ \text{cm}\\ \\ &=72\ \text{cm}^{3} \end{align}\)
b) Pinta-ala:
\(\begin{align} &A_{\text{SUORAK. SÄRMIÖ}}\\ \\ &=2ab+2bc+2ac\\ \\ &=2\cdot6\ \text{cm}\cdot4\ \text{cm}+2\cdot4\ \text{cm}\cdot3\ \text{cm}+2\cdot6\ \text{cm}\cdot3\ \text{cm}\\ \\ &=48\ \text{cm}^{2}+24\ \text{cm}^{2}+36\ \text{cm}^{2}\\ \\ &=108\ \text{cm}^{2} \end{align}\)
c) Merkitään pohjan lävistäjää \(x\). Ratkaistaan pohjan lävistäjä pythagoraan lauseella.
$$x^{2}=a^{2}+b^{2}\quad\mid\sqrt{\ }$$
Pohjan lävistäjä:
$$x=\pm\sqrt{a^2+b^2}$$
d) Ratkaistaan avaruuslävistäjä \(d\) pythagoraan lauseella kolmessa ulottuvuudessa.
$$d^{2}=a^{2}+b^{2}+c^{2}\quad\mid\sqrt{\ }$$
Avaruuslävistäjä:
$$d=\pm\sqrt{a^2+b^2+c^2}$$
Esim. 2
Kuution särmä on 1. Määritä kuution tahkon lävistäjän ja avaruuslävistäjän välisen kulman suuruus.
Kuution särmä, tahkon lävistäjä ja avaruuslävistäjä rajaavat suorakulmaisen kolmion, jonka kateetteina toimivat särmä ja tahkon lävistäjä.
Pohjan lävistäjän pituus \(x\) voidaan ratkaista yhtälöstä:
\(\begin{align} a^{2}+b^{2}&=c^{2}\quad\mid a=1, b=1, c=x\\ \\ 1^{2}+1^{2}&=x^{2}\quad\mid\sqrt{\ }\\ \\ x&=\sqrt{1^2+1^2}=\sqrt{2} \end{align}\)
Tahkon lävistäjän ja avaruuslävistäjän välinen kulma \(\alpha\) voidaan ratkaista yhtälöstä:
\(\begin{align} \tan\alpha&=\dfrac{1}{\sqrt{2}}\\ \\ \alpha&=35{,}264\ldots^{\circ}\approx35{,}3^{\circ} \end{align}\)
Vastaus: \(35{,}3^{\circ}\)
5.2 Lieriö
Lieriö on avaruuskappale, jossa on kaksi yhtenevää ja yhdensuuntaista pohjaa, joita yhdistää vaippa. Särmiö on lieriö, jonka pohja on monikulmio. Suorakulmainen särmiö ja kuutio ovat lieriön erityistapauksia.
Lieriön tilavuus lasketaan lieriön pohjan pinta-ala ja korkeuden tulona.
Lieriön tilavuus
$$V_{\text{lieriö}}=A_{\text{pohja}}h$$
Lieriön pinta-ala lasketaan yhdistämällä lieriön osien pinta-alat.
Lieriön pinta-ala
$$V_{\text{lieriö}}=2A_{\text{pohja}}+A_{\text{vaippa}}$$
Suoran ympyrälieriön vaippa on tasoon avattuna suorakulmio, jonka leveys on pohjaympyrän piiri, \(p\), ja korkeus sama kuin ympyrälieriön korkeus, \(h\). Tällöin vaipan pinta-ala on pohjaympyrän piirin ja korkeuden tulo.
Suoran ympyrälieriön vaipan pinta-ala
$$A_{\text{vaippa}}=ph=2\pi rh$$
Esim. 1
Suoran ympyrälieriön tilavuus on \(240\ \text{cm}^3\) ja pohjan pinta-ala \(60\ \text{cm}^2\). Laske suoran ympyrälieriön vaipan pinta-ala.
Lasketaan ensin lieriön korkeus.
$$ \begin{aligned} V_{\text{lieriö}}&=A_{\text{pohja}}h\quad||:A_{\text{pohja}} \\ h&=\frac{V_{\text{lieriö}}}{A_{\text{pohja}}}\\ h&=\frac{240\ \text{cm}^3}{60\ \text{cm}^2}=4\ \text{cm}\\ \end{aligned} $$
Lasketaan sitten pohjaympyrän säde.
$$ \begin{aligned} A_{\text{pohja}}&=\pi r^{2}\quad\quad\ \ ||:\pi \\ r^{2}&=\frac{A_{\text{pohja}}}{\pi}\quad||\sqrt{}\\ r&=\pm\sqrt{\frac{A_{\text{pohja}}}{\pi}}\\ r&=\pm\sqrt{\frac{60\ \text{cm}^2}{\pi}}\\ \end{aligned} $$
Säteen lukuarvo on positiivinen.
Lasketaan lopuksi vaipan pinta-ala.
$$ \begin{aligned} A_{\text{vaippa}}&=2\pi rh\\ &=2\pi\sqrt{\frac{60\ \text{cm}^2}{\pi}}\cdot 4\ \text{cm}\\ &=109{,}83\ \text{cm}^2\approx 110\ \text{cm}^2\\ \end{aligned} $$
Vastaus: Vaipan pinta-ala on noin \(110\ \text{cm}^2\).
5.3 Kartio
Kartio on avaruuskappale, jossa on pohja ja huippu sekä niitä yhdistävä vaippa. Pyramidi on kartio, jonka pohja on monikulmio.
Kartion tilavuus lasketaan pohjan pinta-ala kertaa korkeus jaettuna kolmella (kolmella jakaminen on sama kuin yksikolmasosalla kertominen).
Kartion tilavuus
$$V_{\text{kartio}}=\frac{A_{\text{pohja}}h}{3}=\frac{1}{3}A_{\text{pohja}}h$$
Kartion pinta-ala lasketaan yhdistämällä kartion osien pinta-alat.
Kartion pinta-ala
$$A_{\text{kartio}}=A_{\text{pohja}}+A_{\text{vaippa}}$$
Suoran ympyräkartion vaipan pinta-ala lasketaan kaavalla \(\pi rs\), missä \(r\) on kartion pohjaympyrän säde ja \(s\) on kartion sivujanan pituus.
Suoran ympyräkartion vaipan pinta-ala
$$A_{\text{vaippa}}=\pi rs$$
Esim. 1
Suoran ympyräkartion leveys on \(10\ \text{cm}\) ja korkeus \(20\ \text{cm}\). Laske tilavuus ja pinta-ala.
Lasketaan pohjaympyrän säde:
\(\begin{align} r&=\dfrac{d}{2}\\ &=\dfrac{10\ \text{cm}}{2}\\ &=5\ \text{cm} \end{align}\)
Lasketaan kartion tilavuus:
\(\begin{align} V_{\text{kartio}}&=\dfrac{1}{3}A_{\text{pohja}}h \quad\mid A_{\text{pohja}}=\pi r^{2}\\ &=\dfrac{1}{3}\pi r^{2}h\quad\quad\mid r=5\ \text{cm}, h=20\ \text{cm}\\ &=\dfrac{1}{3}\pi (5\ \text{cm})^{2}\cdot20\ \text{cm}\\ &=\dfrac{500\pi}{3}\pi\ \text{cm}^{3}\\ &=523{,}59\ldots\ \text{cm}^{3}\\ &\approx520\ \text{cm}^{3} \end{align}\)
Kartion pinta-alan laskemiseksi on ratkaistava kartion sivujanan \(s\) pituus.
\(\begin{align} a^{2}+b^{2}&=c^{2}\quad\quad\mid a=r=5\ \text{cm}, b=h=20\ \text{cm}, c=s\\ (5\ \text{cm})^{2}+(20\ \text{cm})^{2}&=s^{2}\quad\quad\mid \sqrt{\ }\\ s&=\pm\sqrt{(5\ \text{cm})^{2}+(20\ \text{cm})^{2}}\\ s&=\pm\sqrt{425\ \text{cm}^{2}}\\ s&=\pm\sqrt{425}\ \text{cm} \end{align}\)
Pituus on positiivista.
Kartion pinta-ala:
\(\begin{align} A_{\text{kartio}}&=A_{\text{pohja}}+A_{\text{vaippa}}\\ &=\pi r^{2}+\pi r s \quad\quad\mid r=5\ \text{cm}, s=\sqrt{425}\ \text{cm}\\ &=\pi \cdot(5\ \text{cm})^{2}+\pi \cdot5\ \text{cm}\cdot\sqrt{425}\ \text{cm}\\ &=402{,}36\ldots\ \text{cm}^{2}\\ &\approx400\ \text{cm}^{2}\\ \end{align}\)
Vastaus: Tilavuus on \(520\ \text{cm}^{3}\) ja pinta-ala \(400\ \text{cm}^{2}\).
Esim. 2
Jogurttipikari on esimerkki kappaleesta, joka on muodoltaan leikattu kartio. Pikarin kannen leveys on \(6{,}5\ \text{cm}\), pohjan leveys \(5{,}0\ \text{cm}\) ja korkeus \(7{,}0\ \text{cm}\). Laske pikarin tilavuus.
Mallikuva (poikkileikkaus):
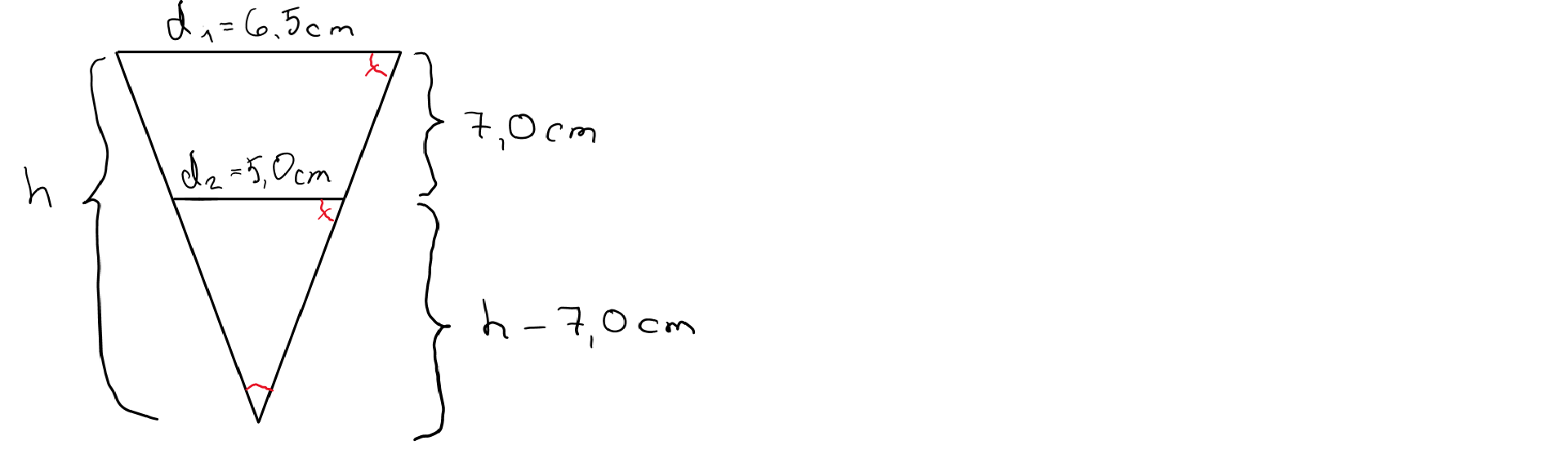
Kuvan tasakylkiset kolmiot ovat yhdenmuotoisia (kk-lause).
Korkeus \(h\) voidaan ratkaista verrantoyhtälöstä:
\(\begin{align} \dfrac{h}{h-7{,}0\ \text{cm}}&=\dfrac{6{,}5\ \text{cm}}{5{,}0\ \text{cm}}\\ h\cdot5{,}0\ \text{cm}&=(h-7{,}0\ \text{cm})\cdot6{,}5\ \text{cm}\\ h\cdot5{,}0\ \text{cm}&=h\cdot6{,}5\ \text{cm}-7{,}0\ \text{cm}\cdot6{,}5\ \text{cm}\\ h\cdot5{,}0\ \text{cm}-h\cdot6{,}5\ \text{cm}&=-45{,}5\ \text{cm}^{2}\\ -h\cdot1{,}5\ \text{cm}&=-45{,}5\ \text{cm}^{2}\\ h&=\dfrac{-45{,}5\ \text{cm}^{2}}{-1{,}5\ \text{cm}}=\dfrac{45{,}5}{1{,}5}\ \text{cm} \end{align}\)
Pohjaympyröiden (eli kannen ja pohjan) säteet:
\(\begin{align} r_1&=\dfrac{d_1}{2}=\dfrac{6{,}5\ \text{cm}}{2}=3{,}25\ \text{cm}\\ \\ r_2&=\dfrac{d_2}{2}=\dfrac{5{,}0\ \text{cm}}{2}=2{,}5\ \text{cm} \end{align}\)
Jogurttipikarin tilavuus:
\(\begin{align} V&=V_{1}-V_{2}\\ &=\dfrac{1}{3}\pi r_{1}^{2}h-\dfrac{1}{3}\pi r_{2}^{2}(h-7{,}0\ \text{cm})\\ &=\dfrac{1}{3}\pi (3{,}25\ \text{cm})^{2}h-\dfrac{1}{3}\pi (2{,}5\ \text{cm})^{2}\left(\dfrac{45{,}5}{1{,}5}\ \text{cm}-7{,}0\ \text{cm}\right)\\ &=182{,}801\ldots\ \text{cm}^{3}\approx180\ \text{cm}^{3}=180\ \text{ml}=1{,}8\ \text{dl} \end{align}\)
Vastaus: Jogurttipikarin tilavuus on noin 1,8 dl.
5.4 Pallo
Pallo on kappale, jonka pinnan jokainen piste on säteen etäisyydellä pallon keskipisteestä.
Pallon tilavuus
$$V=\frac{4\pi r^{3}}{3}=\frac{4}{3}\pi r^{3}$$
Pallon pinta-ala
$$A=4\pi r^{2}$$
Kun palloa leikataan tasolla, syntyvät osat ovat pallosegmenttejä ja pinnat kalotteja.
Kaksi yhdensuuntaista tasoa rajaavat pallosta pinnan, jota kutsutaan vyöhykkeeksi.
Pallosegmentin tilavuus
$$V=\pi h^{2} \left(r-\frac{h}{3}\right)$$
Kalotin ja vyöhykkeen pinta-ala
$$A=2\pi rh$$
Esim. 1

Lähde: pixabay.com.
Millenium dome (nyk. O2 Arena) on yksi Lontoon maamerkeistä. Sen halkaisija on 365 m ja korkeus 52 m. Rakennelma on likimain pallosegmentin muotoinen. Laske rakennelman tilavuus kuutiometreinä kahden merkitsevän numeron tarkkuudella.
Mallikuva (poikkileikkaus):
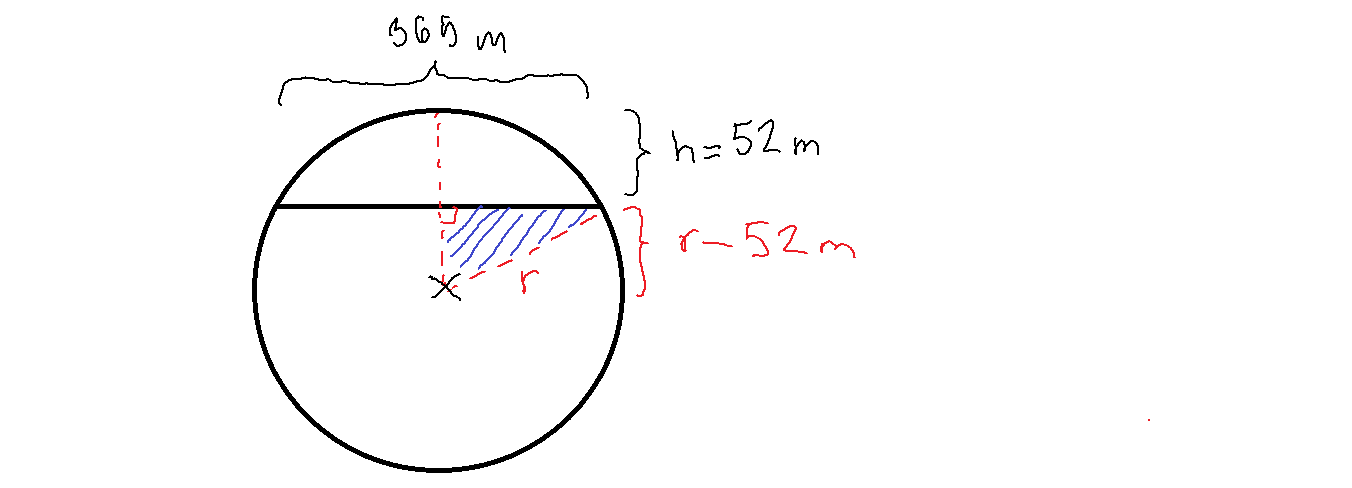
Ratkaistaan pallon säde \(r\) Pythagoraan lauseen avulla:
\(\begin{align} a^{2}+b^{2}&=c^{2}\\ (r-52\ \text{m})^{2}+\left(\dfrac{365\ \text{m}}{2}\right)^{2}&=r^{2} \quad\mid\text{CAS-laskin}\\ r&=346{,}25\ldots\ \text{m} \end{align}\)
Lasketaan tilavuus pallosegmentin tilavuuden kaavalla:
\(\begin{align} V&=\pi h^{2}\left(r-\dfrac{h}{3}\right)\\ &=\pi(52\ \text{m})^{2}\left(346{,}25\ldots\ \text{m}-\dfrac{52\ \text{m}}{3}\right)\\ &=2\ 794\ 103{,}18\ldots\ \text{m}^{3}\\ &\approx2\ 800\ 000\ \text{m}^{3} \end{align}\)
Vastaus: Rakennelman tilavuus on noin \(2\ 800\ 000\ \text{m}^{3}\).
Esim. 2
Tulossa myöhemmin.
Tulossa myöhemmin.