Analyyttinen geometria ja vektorit (MAA4)
Laajuus
3 op
Yleiset tavoitteet (LOPS 2021)
Moduulin tavoitteena on, että opiskelija
- ymmärtää, kuinka analyyttinen geometria luo yhteyksiä geometristen ja algebrallisten käsitteiden välille
- ymmärtää yhtälön geometrisen merkityksen
- osaa ratkaista muotoa \(\left| f(x)\right| =a\) tai \(\left| f(x) \right| = \left| g(x)\right|\) olevia itseisarvoyhtälöitä
- ymmärtää vektorikäsitteen ja perehtyy vektorilaskennan perusteisiin
- osaa tutkia kaksiulotteisen koordinaatiston pisteitä, etäisyyksiä ja kulmia vektoreiden avulla
- osaa ratkaista tasogeometrian ongelmia vektoreiden avulla
- osaa käyttää ohjelmistoja käyrien ja vektoreiden tutkimisessa sekä niihin liittyvissä sovelluksissa.
Keskeiset sisällöt (LOPS 2021)
- käyrän yhtälö
- suoran, ympyrän ja paraabelin yhtälö
- yhtälöryhmä
- suorien yhdensuuntaisuus ja kohtisuoruus
- itseisarvoyhtälö
- pisteen etäisyys suorasta
- vektoreiden perusominaisuudet
- tason vektoreiden yhteen- ja vähennyslasku sekä tason vektorin kertominen luvulla
- tason vektoreiden pistetulo, tason vektoreiden välinen kulma
Aikataulu
Suoritus
- osallistuminen
- tehtävien tekeminen
- 3 osakoetta
Arviointi
- tehtävien asianmukainen ja jatkuva tekeminen
- Opintojakson suorittaminen edellyttää vähintään 60 oppikirjan tehtävän asianmukaista tekemistä tai 23 pistettä kokeesta.
- Poissaolot korvataan tehtävillä. Jos poissaoloja on kuusi, edellytetään opintojakson suorittamiseksi vähintään 120 tehtyä oppikirjan tehtävää.
- Tehdyistä tehtävistä saa lisäpisteitä seuraavasti:
- osakokeista max. 144 p = 72 p + 36 p + 36 p
- yhteensä max. 153 p
- 30 % arviointi
| Tehtävät | Lisäpisteet |
|---|---|
| 60 | 3 |
| 90 | 5 |
| 120 | 7 |
| 150 | 9 |
| Pisteet | Arvosana | Muuta |
|---|---|---|
| 0 - 22* | i \(\to\) K | Pakko täydentää. |
| 23 - 42** | 4 | Oikeus täydentää. |
| 43 - 62 | 5 | |
| 63 - 82 | 6 | |
| 83 - 102 | 7 | |
| 103 - 122 | 8 | |
| 123 - 142 | 9 | |
| 143 - 153 | 10 |
* ja vähimmäistehtävävaatimus ei täyty.
** tai vähimmäistehtävävaatimus täyttyy.
Keskeyttäminen
Opettaja keskeyttää opiskelijan opintojakson, jos
- opiskelija niin pyytää
- opiskelija ei ole läsnä opintojakson kahdella ensimmäisellä opetuskerralla ja opiskelija ei ole yhteydessä opettajaan eikä opettaja saa yhteyttä opiskelijaan.
Opettaja voi keskeyttää opiskelijan opintojakson, jos opiskelijalla on viisi poissaoloa. Tällaiset tilanteet opettaja käy läpi tapauskohtaisesti ja on ennen lopullista keskeytystä yhteydessä opiskelijaan.
Keskeyttämisestä opettaja merkitsee opintojaksosta opiskelijalle K-merkinnän Wilmaan ja poistaa opiskelijan sen jälkeen Wilman ryhmästä. Opettaja lähettää keskeyttämisestä viestin opiskelijalle, alaikäisen opiskelijan huoltajalle, ryhmänohjaajalle ja opolle.
1 YHTÄLÖITÄ
1.1 Itseisarvo
Luvun itseisarvo on luvun etäisyys nollasta lukusuoralla.
Itseisarvon määritelmä
$$\left| a\right| = \begin{cases} a,\ \text{kun}\ a\geq0\\ -a,\ \text{kun}\ a\lt0\\ \end{cases}$$
Määritelmän mukaan, jos luku \(a\) on
- suurempi tai yhtä suuri kuin 0, luvun \(a\) itseisarvo on luku \(a\) itse,
- pienempi kuin 0, luvun \(a\) itseiarvo on luvun \(a\) vastaluku \(-a\).
Esim. 1
Määritä luvun itseisarvo.
a) \(\frac{1}{5}\) b) \(0\) c) \(-\frac{1}{5}\) d) \(\sqrt{2}-1\) e) \(1-\sqrt{2}\)
Itseisarvon ominaisuuksia
1) \(\left| a\right|\geq0\)
2) \(\left| a\right|=\left| -a\right|\)
3) \(\left| ab\right|=\left| a\right| \left| b\right|\)
4) \(\left| \frac{a}{b}\right|=\frac{\left| a\right|}{\left| b\right|}\)
Kahden luvun erotuksen itseisarvo on lukujen etäisyys toisistaan lukusuoralla.
Lukujen \(a\) ja \(b\) etäisyys
Lukujen \(a\) ja \(b\) välinen etäisyys toisistaan lukusuoralla on lukujen erotuksen itseisarvo$$\left| a-b \right|.$$
Esim. 2
Ilmatieteen laitoksen mukaan lämpötilan ennätykset Suomessa ovat 37,2 ja -51,5 astetta celsiusta. Mikä on korkeimman ja matalimman mitatun lämpötilan välinen ero celsiusasteina?
Esim. 3
Määritä lukujen \(\sqrt{2} -1\) ja \(1-\sqrt{2}\) välinen etäisyys.
CAS-laskimella itseisarvolausekkeita voidaan sieventää abs()-komennolla, käyttämällä laskimen näppäimistöltä löytyvää syöttöpohjaa tai tietokoneen näppäimistöllä alt gr + |.
Esim. 4
Sievennä käsin ja tarkista CAS-laskimella.
a) \(\left| 2x \right| + \left| -2x \right|\)
b) \(\left| 2x-2 \right|\), kun \(x<1\)
Huom.
Ehto \(x<1\) voidaan ilmoittaa CAS-laskimelle esimerkiksi näin:
oleta(\(x<1,\left| 2x-2 \right|\)).
1.2 Itseisarvoyhtälö
Yhtälön \(\left| f(x)\right| =a\) ratkaiseminen
(1) Jos \(a\geq0\), puretaan yhtälö kahdeksi yhtälöksi ja ratkaistaan molemmat:
$$\left| f(x)\right| =a$$
$$f(x)=a\quad \text{tai}\quad f(x)=-a$$
(2) Jos \(a<0\), yhtälöllä ei ole ratkaisua.
Esim. 1
Ratkaise itseisarvoyhtälö.
a) \(\left| 2x+5 \right| = 9\)
b) \(\left| 3x+4 \right| = -8\)
Vastaus: a) \(x=2\) tai \(x=-7\) b) Ei ratkaisua.
Yhtälön \(\left| f(x)\right| = \left| g(x)\right|\) ratkaiseminen
Puretaan yhtälö kahdeksi yhtälöksi ja ratkaistaan molemmat:
$$\left| f(x)\right| = \left| g(x)\right|$$
$$f(x)=g(x)\quad \text{tai}\quad f(x)=-g(x)$$
Toisin sanoen funktioiden \(f(x)\) ja \(g(x)\) arvot ovat samat tai toistensa vastaluvut.
Esim. 2
Ratkaise itseisarvoyhtälö \(\left| x^{2}+3 \right| = \left| 2x+2 \right|\).
Vastaus: \(x=2\)
1.3 Yhtälöryhmä
Yhtälöryhmä tarkoittaa kahta tai useampaa yhtälöä, joissa on yksi tai useampia muuttujia. Kahden yhtälön tapauksessa puhutaan yleensä yhtälöparista. Yhtälöryhmän ratkaiseminen tarkoittaa, että selvitetään kaikki luvut, jotka toteuttavat yhtälöryhmän kaikki yhtälöt.
Huom.
Yhtälöryhmä voidaan ratkaista vain, jos muuttujia on korkeintaan yhtä monta kuin yhtälöitä.
Esim.
Ratkaise yhtälöryhmä, jossa on kolme yhtälöä ja kaksi muuttujaa.
$$ \begin{cases} \ \ x+2y=\ \ \ 8\\ 2x+\ \ y=-2\\ \ \ x+\ \ y=\ \ \ 2 \end{cases} $$
Vastaus: \(x=-4\ \text{ja}\ y=6\).
Esim.
Ratkaise yhtälöryhmä, jossa on kolme yhtälöä ja kolme muuttujaa.
$$ \begin{cases} 3x-\ \ y+2z=0\\ 2x+4y-2z=0\\ 5x+2y+\ \ z=4 \end{cases} $$
Vastaus: \(x=-6,\ y=10\ \text{ja}\ z=14\).
Huom.
CAS-laskimella yhtälöryhmä voidaan ratkaista käyttäen solve()- tai ratkaise()-komentoa. Vaikkapa edellisen esimerkin yhtälöryhmä voitaisiin ratkaista GeoGebralla:
solve(\( \left\{3x-y+2z=0,2x+4y-2z=0,5x+2y+z=4\right\} , \left\{x,y,z \right\} \))
2 Jana ja suora
2.1 Jana
Janan pituuden \(d\) laskeminen
$$d=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}$$
Janan keskipisteen \(M\) koordinaatit
$$M=\left(\frac{x_{1}+x_{2}}{2},\frac{y_{1}+y_{2}}{2}\right)$$
Esim. 1
Janan päätepisteiden koordinaatit ovat \(\left(-1,4\right)\) ja \(\left(3,1\right)\).
a) Laske janan pituus.
b) Määritä janan keskipisteen koordinaatit.
Vastaus:
a) \(5\)
b) \(\left(1,\frac{5}{2}\right)\)
2.2 Suora
Suoran kulmakertoimen arvo voidaan määrittää, jos tunnetaan kahden suoran pisteen koordinaatit.
Kulmakerroin \(k\)
$$k=\frac{\Delta y}{\Delta x}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$$
Esim. 1
Määritä suoran kulmakerroin, kun suora kulkee pisteiden \((-1,-2)\) ja \((2,4)\) kautta.
Vastaus: \(k=2\)
Suuntakulma on toinen mahdollinen tapa ilmaista suoran suunta. Suuntakulma on suoran ja x-akselin positiivisen suunnan välinen kulma. Suuntakulman \(\alpha\) arvo on aina \(-90^{\circ}<\alpha\leq90^{\circ}\).
Suuntakulman \(\alpha\) ja kulmakertoimen \(k\) välinen yhteys
(1) Kun \(-90^{\circ}<\alpha<90^{\circ}\),$$k=\tan\alpha=\frac{\Delta y}{\Delta x}.$$
(2) Kun \(\alpha=90^{\circ}\), suora on pystysuora (ei kulmakerrointa).
Esim. 2
Määritä suoran suuntakulma, kun suoran kulmakerroin on
a) \(k=-\frac{2}{3}\)
b) \(k=2\).
Vastaus: a) \(-33{,}7^{\circ}\) b) \(63{,}4^{\circ}\).
Huom.
Kulmakerroin ja suuntakulma ilmaisevat suoran suunnan.
$$ \begin{array}{lll} \hline \mathbf{kulmakerroin} & \mathbf{suuntakulma} & \mathbf{suoran\ suunta}\\ \hline k>0 & 0^{\circ}<\alpha<90^{\circ} & \text{nouseva}\\ k=0 & \alpha=0^{\circ} & \text{vaakasuora}\\ k<0 & -90^{\circ}<\alpha<0^{\circ} & \text{laskeva}\\ \text{ei kulmakerrointa} & \alpha=90^{\circ} & \text{pystysuora}\\ \hline \end{array} $$
Lisäksi mitä suurempi on \(\left|k\right|\), sitä jyrkemmin suora kulkee.
Suoran yhtälö voidaan määrittää, jos tunnetaan kulmakertoimen arvo ja yhden suoran pisteen koordinaatit tai jos tunnetaan kahden suoran pisteen koordinaatit.
Pisteen \((x_{0},y_{0})\) kautta kulkevan suoran yhtälö
$$y-y_{0}=k(x-x_{0})$$
Esim. 3
Suora, jonka kulmakerroin on \(k=-2\), kulkee pisteen \((4,-1)\) kautta.
a) Määritä suoran yhtälö.
b) Tutki, onko piste \((-1,9)\) suoralla.
Vastaus: a) Suoran yhtälö on \(y=-2x+7\). b) Piste \((-1,9)\) on suoralla.
Esim. 4
Suora kulkee pisteiden \((-2,1)\) ja \((3,6)\) kautta. Määritä suoran yhtälö. Ilmoita vastaus normaalimuodossa.
Vastaus: Suoran yhtälö normaalimuodossa on \(x-y+3=0\).
Huom.
CAS-laskimella voidaan piirtoalueelle piirtää suora työkalujen avulla tai syöttämällä suoran yhtälö algebraikkunaan. Piirtoalueelle työkalujen avulla piirretyn suoran yhtälö on luettavissa algebraikkunasta asetuksista valitsemalla joko ratkaistussa muodossa, parametrimuodossa tai normaalimuodossa.
2.3 Suorien leikkauspiste
Esim. 1.
Määritä suorien \(2x+4y=-2\) ja \(3x+5y=-1\) leikkauspiste.
Ratkaisu:
Suorien leikkauspisteen koordinaatit ovat lukupari, joka toteuttaa suorien yhtälöistä muodostetun yhtälöparin.
\( \ \ \ \left\{ \begin{aligned} 2x+4y&=-2\quad\quad\mid\ \cdot 3 \\ 3x+5y&=-1\quad\quad\mid\ \cdot (-2) \\ \end{aligned} \right. \)
\(
\underline{\begin{array}\ \\+\end{array}\left\{
\begin{aligned}
\cancel{6x}+12y&=-6 \\
\cancel{-6x}-10y&=2 \\
\end{aligned}
\right.}
\)
\(
\qquad \qquad \qquad 2y=-4
\)
\( \qquad \qquad \qquad \ \ y=\frac{-4}{2}=-2 \)
Sijoitetaan \(y=-2\) alkuperäisistä yhtälöistä ylempään.
\( \begin{aligned} 2x+4\cdot (-2)&=-2\\ 2x-8&=-2\\ 2x&=-2+8\\ 2x&=6\\ x&=\frac{6}{2}=3 \end{aligned} \)
Vastaus: \(\left(3, -2\right)\).
2.4 Yhdensuuntaiset ja leikkaavat suorat
(1) Suorat \(s_1\) ja \(s_2\) ovat yhdensuuntaiset, mutta eivät yhdy, eli \(s_1\parallel s_2\)
- Kulkevat yhdensuuntaisina erillään
- Ei yhteisiä pisteitä
- Kulmakertoimet samat (ja eri vakiotermit tai molemmat pystysuoria)
- Suorat eivät rajaa kulmaa
(2) Suorat \(s_1\) ja \(s_2\) yhtyvät eli \(s_1=s_2\)
- Edellisen erityistapaus: kulkevat yhdensuuntaisina päällekkäin
- Äärettömän monta yhteistä pistettä
- Yhtälöt samat (eli sama kulmakerroin ja vakiotermi tai molemmat pystysuoria)
- Suorien välinen kulma \(0^{\circ}\)
(3) Suorat \(s_1\) ja \(s_2\) eivät ole yhdensuuntaiset eli \(s_1\nparallel s_2\)
- Leikkaavat
- Yksi yhteinen piste
- Eri kulmakertoimet
- Suorien välinen kulma \(\left]0^{\circ},90^{\circ}\right]\)
(4) Suorat \(s_1\) ja \(s_2\) ovat kohtisuorassa toisiaan vastaan eli \(s_1\perp s_2\)
- Edellisen erityistapaus: leikkaavat toisensa suorassa kulmassa (suorat ovat toistensa normaaleja)
- Yksi yhteinen piste
- Kulmakertoimien tulo on \(k_1\cdot k_2=-1\)
- Suorien välinen kulma \(90^{\circ}\)
Yhdensuuntaisuusehto
Suorat ovat yhdensuuntaiset, jos niillä on sama kulmakerroin tai molemmat suorat ovat pystysuoria.
Kohtisuoruusehto
Suorat ovat toistensa normaaleja (eli kohtisuoria), jos niiden kulmakertoimien tulo on \(-1\) tai toinen on vaakasuora ja toinen pystysuora.
Esim.
Määritä yhtälö pisteen \((-1,2)\) kautta kulkevalle suoralle, joka on suoran \(4x-2y-10=0\)
a) kanssa yhdensuuntainen
b) normaali.
Vastaus: a) \(y=2x+4\) b) \(y=-\frac{1}{2}x+\frac{3}{2}\)
Suorien välinen kulma tarkoittaa kahden suoran leikatessa muodostuvista kulmista pienempää. Kulman suuruus voidaan laskea suorien suuntakulmien avulla tai alla olevalla kaavalla.
Suorien välinen kulma \(\varphi\)
Kun \(0^{\circ}\leq\varphi<90^{\circ}\),$$\tan \varphi=\left|\frac{k_{1}-k_{2}}{1+k_{1}k_{2}} \right|$$
Esim.
Määritä suorien yhteiset pisteet ja välinen kulma.
a) \(6x-3y+9=0\) ja \(2x-3y-3=0\)
b) \(6x-3y+9=0\) ja \(y=2x+3\)
Vastaus:
a) Yhteinen piste \((-3,-3)\) ja välinen kulma \(29{,}7^{\circ}\)
b) Äärettömän monta yhtälön \(y=2x+3\) määräämää yhteistä pistettä ja välinen kulma \(0^{\circ}\)
2.5 Pisteen etäisyys suorasta
Pisteen \((x_{0},y_{0})\) etäisyys suorasta tarkoittaa pisteen lyhintä eli kohtisuoraa etäisyyttä suorasta. Etäisyys voidaan määrittää pisteen \((x_{0},y_{0})\) kautta kulkevan suoran normaalin avulla tai alla olevalla kaavalla.
Pisteen etäisyys suorasta
Pisteen \((x_{0},y_{0})\) etäisyys \(d\) suorasta \(ax+by+c=0\)
$$d=\frac{\left|ax_{0}+by_{0}+c\right|}{\sqrt{a^{2}+b^{2}}}$$
Esim.
Määritä pisteen \((1,6)\) etäisyys suorasta \(3x-4y+1=0\).
Vastaus: \(4\)
Esim.
Määritä suoran yhtälö, kun suora on \(2\) yksikön etäisyydellä suorasta \(4x+3y-6=0\).
Vastaus: \(4x+3y-16=0\) ja \(4x+3y+4=0\)
Määritelmä
Janan keskinormaali on normaali, joka kulkee janan keskipisteen kautta.
Lause
Janan keskinormaalin piste on yhtä kaukana janan päätepisteistä.
Esim.
Janan \(AB\) päätepisteet ovat \(A(-4,5)\) ja \(B(-2,3)\). Missä pisteessä janan \(AB\) keskinormaali leikkaa x-akselin.
Vastaus: \((-7,0)\)
Määritelmä
Kulmanpuolittaja on puolisuora, joka jakaa kulman kahteen yhtä suureen osaan.
Lause
Kulmanpuolittajan piste on yhtä kaukana kulman kyljistä.
Esim.
Määritä suorien \(8x-4y+3=0\) ja \(x-2y-1=0\) kulmanpuolittajien yhtälöt.
Vastaus: \(4x+4y+7=0\) ja \(12x-12y-1=0\)
3 YMPYRÄ
3.1 Ympyrän yhtälön keskipistemuoto
Esim. 1
Piirrä ympyrä, jonka keskipiste on \((x_0,y_0)=(2,1)\) ja säde \(r=5\). Johda ympyrälle yhtälö.
Piirretään kuva GeoGebralla.
Johdetaan ympyrälle yhtälö käyttäen kahden pisteen välisen etäisyyden kaavaa, kun pisteet ovat ympyrän keskipiste (2,1), eräs kehän piste (x,y) ja kahden pisteen välinen etäisyys on säde, 5 yksikköä.
\( \begin{align} \left|AB\right|&=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)}\\ 5&=\sqrt{\left(x-2\right)^2+\left(y-1\right)^2}\\ \sqrt{\left(x-2\right)^2+\left(y-1\right)^2}&=5\ \mid\left(\right)^2\\ \left(x-2\right)^2+\left(y-1\right)^2&=5^2\\ \left(x-2\right)^2+\left(y-1\right)^2&=25 \end{align} \)
Vastaus: Ympyrän yhtälö on \((x-2)^2+(y-1)^2=5^2\) (keskipistemuoto).
Ympyrän yhtälön keskipistemuoto
$$(x-x_0)^2 +(y-y_0)^2=r^2,$$ missä \((x_0,y_0)\) on ympyrän keskipiste ja \(r\) on ympyrän säde.
Esim. 2
Tutki laskemalla, ovatko pisteet \((-1,-3)\) ja \((-3,2)\) ympyrän \((x-2)^2+(y-1)^2=5^2\) kehällä, kehän sisäpuolella vai sen ulkopuolella.
Tutkitaan, toteuttaako piste \((-1,-3)\) ympyrän yhtälön.
\( \begin{align} \left(-1-2\right)^2+\left(-3-1\right)^2&=5^2\\ \left(-3\right)^2+\left(-4\right)^2&=25\\ 9+16&=25\\ 25&=25 \quad \text{(tosi)} \end{align} \)
Piste \((-1,-3)\) on kehällä.
Tutkitaan, toteuttaako piste \((-3,2)\) ympyrän yhtälön.
\( \begin{align} \left(-3-2\right)^2+\left(2-1\right)^2&=5^2\\ \left(-5\right)^2+1^2&=25\\ 25+1&=25\\ 26&=25 \quad \text{(epätosi)} \end{align} \)
Piste \((-3,2)\) ei ole kehällä. Koska yhtälön vasen puoli (kahden pisteen etäisyyden neliö) on suurempi kuin oikea puoli (säteen neliö), on piste \((-3,2)\) kehän ulkopuolella.
Vastaus: Piste \((-1,-3)\) on ympyrän kehällä ja piste \((-3,2)\) on kehän ulkopuolella.
Esim. 3
Ympyrän yhtälö on \((x+3)^2+y^2=4\). Määritä ympyrän keskipisteen koordinaatit ja säteen pituus piirtämällä sekä laskemalla.
Piirtämällä: GeoGebra.
Laskemalla:
Muokataan ympyrän yhtälöä vastaamaan ympyrän yhtälön keskipistemuodon kaavaa:
\( \begin{align} (x-x_0)^2+(y-y_0)^2&=r^2.\\ \\ \left(x+3\right)^2+y^2\quad \quad \ \ &=4\\ \left(x-\left(-3\right)\right)^2+\left(y-0\right)^2&=2^2 \end{align} \)
Vastaus: Ympyrän keskipiste on \((-3,0)\) ja säde \(2\).
3.2 Ympyrän yhtälön normaalimuoto
Ympyrän yhtälö voidaan esittää myös normaalimuodossa eli siten, että kaikki nollasta eroavat termit on järjestelty yhtälön vasemmalle puolelle. Ympyrän yhtälön normaalimuodosta käytetään myös nimitystä ympyrän yhtälön yleinen muoto.
Esim. 1
Ympyrän yhtälö on keskipistemuodossa \((x-2)^2+(y-1)^2=5^2\). Saata yhtälö normaalimuotoon.
\( \begin{align} \left(x-2\right)^2+\left(y-1\right)^2&=5^2 \mid (a-b)^2=a^2-2ab+b^2\\ x^2-2\cdot x\cdot2+2^2+y^2-2\cdot y\cdot1+1^2&=25\\ x^2-4x+4+y^2-2y+1&=25 \mid -25\\ x^2+y^2-4x-2y+4+1-25&=0\\ x^2+y^2-4x-2y-20&=0 \end{align} \)
Vastaus: \(x^{2}+y^{2}-4x-2y-20=0\) (normaalimuoto)
Ympyrän yhtälön normaalimuoto (eli yleinen muoto)
$$x^{2}+y^{2}+ax+by+c=0,$$ missä \(a\), \(b\) ja \(c\) ovat vakioita.
Esim. 2
Ympyrän yhtälö on normaalimuodossa \(x^{2}+y^{2}+6x-4y-17=0\). Saata yhtälö keskipistemuotoon.
Vastaus: \((x+3)^2+(y-2)^2=2^2\)
Huom.
Edellisessä esimerkissä voidaan hyödyntää GeoGebran komentoa TäydennäNeliöön(). Ympyrän yhtälön muotoa voi myös vaihtaa GeoGebrassa kuten suorankin tapauksessa.
3.3 Ympyrän leikkauspisteitä
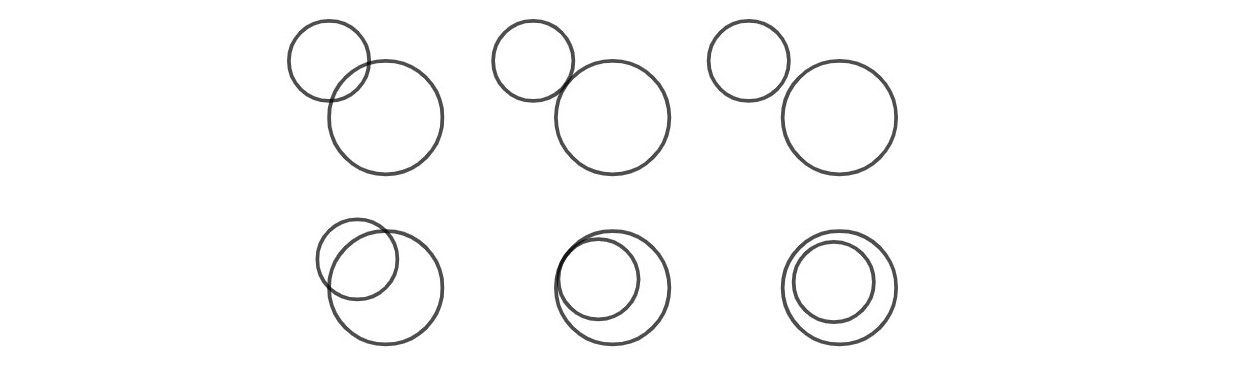
Suoralla ja ympyrällä voi olla 0, 1 tai 2 leikkauspistettä.
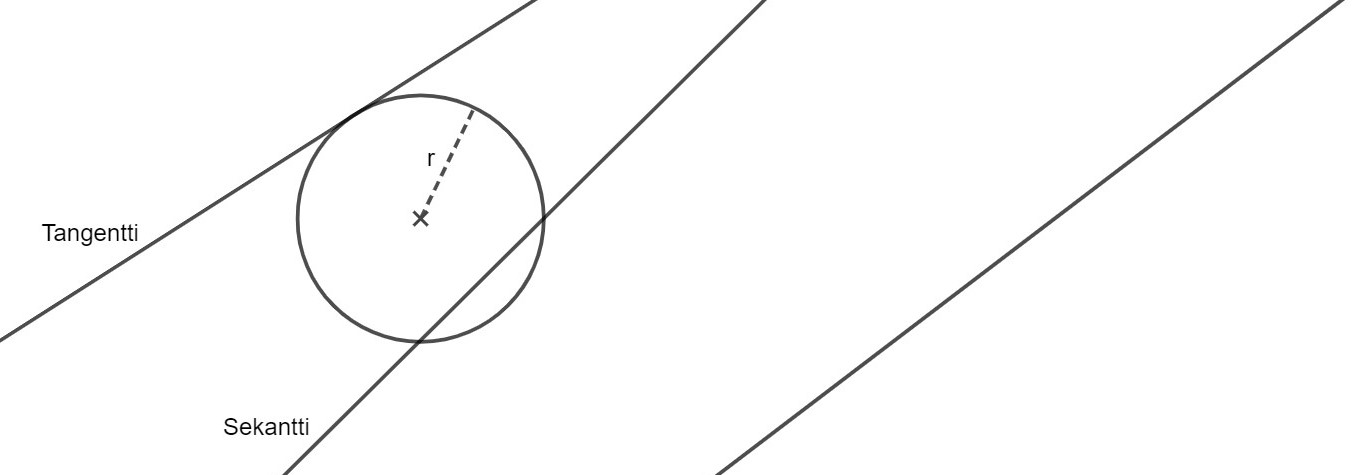
Kahdella ympyrällä voi olla 0, 1 tai 2 leikkauspistettä. Ympyrät voivat sijaita toisiinsa nähden alla kuvatuilla tavoilla.
Esim.
Olkoon suora \(x+y=7\) ja ympyrät \(x^{2}+y^{2}-8x-6y+23=0\) sekä \((x-5)^{2}+(y-2)^{2}=4\). Määritä laskemalla leikkauspisteet
a) suoralle ja ympyrälle \(x^{2}+y^{2}-8x-6y+23=0\)
b) ympyröille.
Vastaus: a) \((3,4)\) ja \((5,2)\) b) \((3,2)\) ja \((5,4)\).
3.4 Ympyrän tangentti
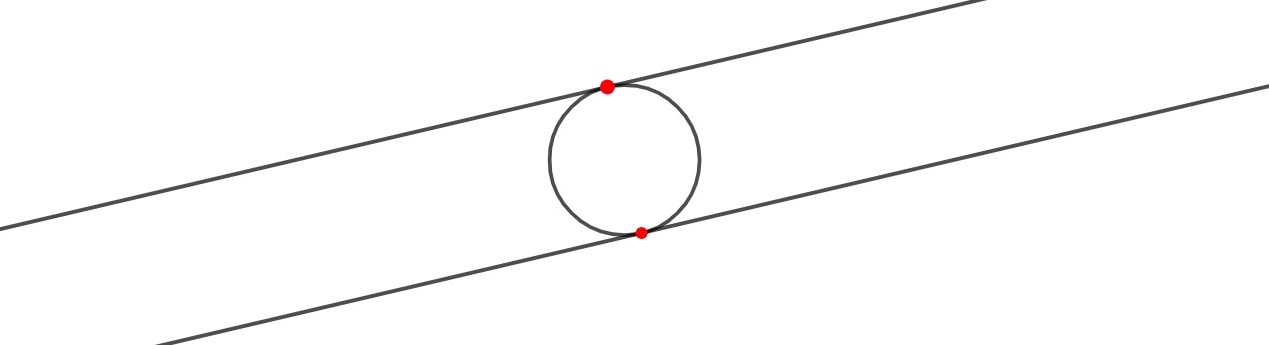
Suora, joka sivuaa (eli leikkaa yhdessä pisteessä) ympyrää, on ympyrän tangentti.
Lause
Tangentti on säteen etäisyydellä ympyrän keskipisteestä.
Lause
Tangentti ja sivuamispisteeseen päättyvä säde ovat kohtisuorassa toisiaan vastaan.
Ympyrän kehällä olevan pisteen kautta voidaan piirtää yksi tangentti.
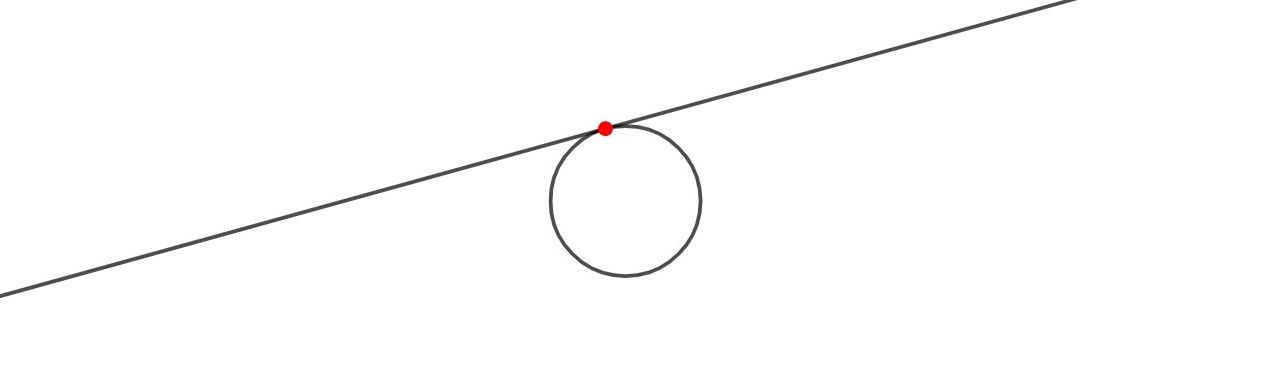
Ympyrän kehän ulkopuolella olevan pisteen kautta voidaan piirtää kaksi tangenttia samalle ympyrälle.
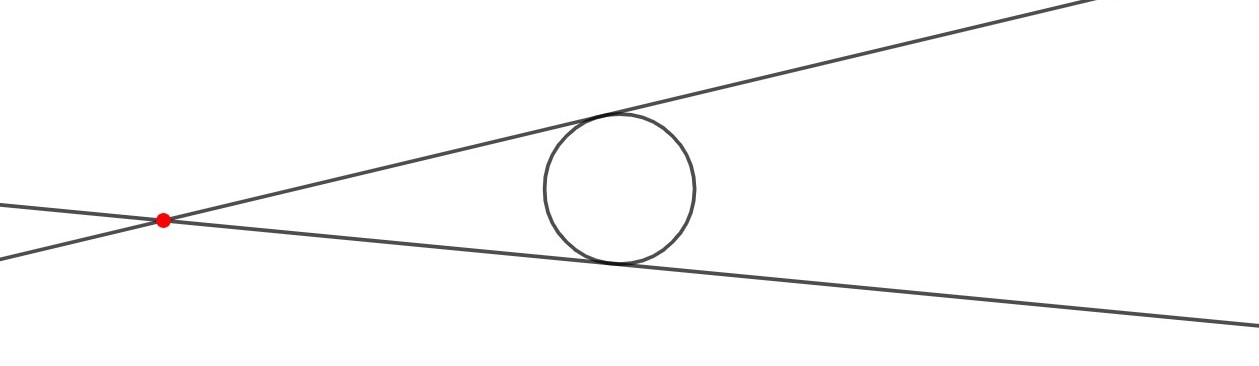
Ympyrälle voidaan piirtää kaksi tangenttia, joilla on keskenään sama kulmakerroin.
Esim.
Osoita, että suora \(y=x+1\) on ympyrän \((x-3)^{2}+(y-2)^{2}=2\) tangentti.
Vihje: On osoitettava, että suoran \(y=x+1\) etäisyys ympyrän ympyrän keskipisteestä on ympyrän säde.
4 PARAABELI
4.1 Paraabelin määritelmä
Paraabeli
Paraabeli on tason pistejoukko, jonka jokainen piste sijaitsee yhtä kaukana paraabelin polttopisteestä ja johtosuorasta.
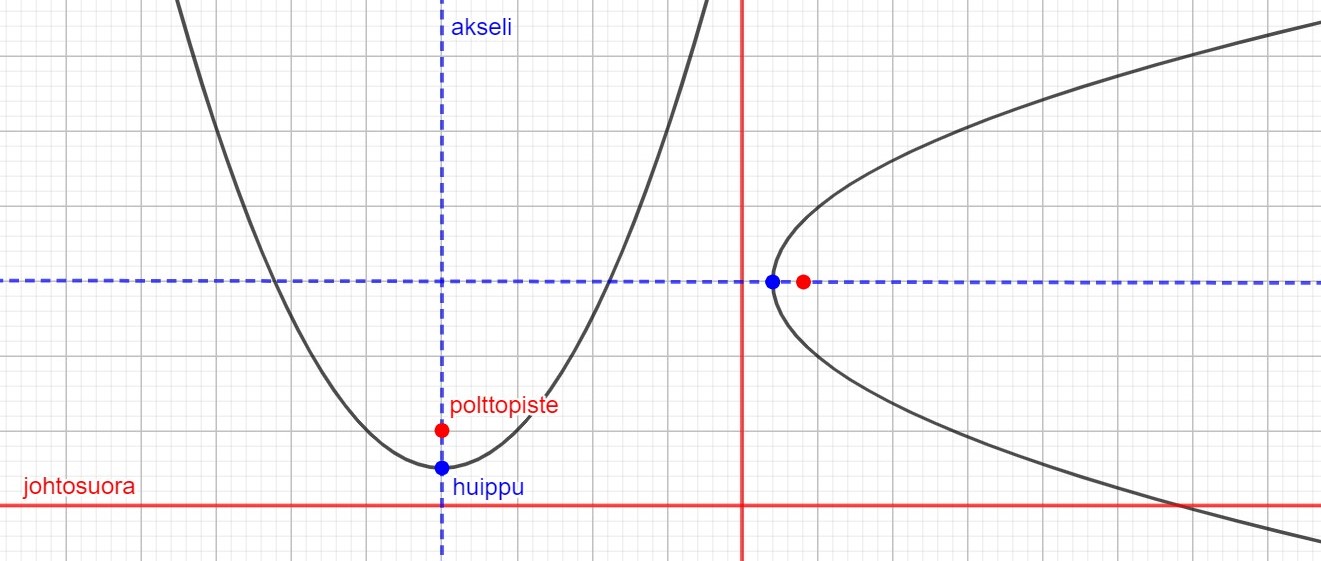
Paraabelin akseli
- on johtosuoran normaali
- kulkee polttopisteen kautta
- on paraabelin symmetria-akseli
Paraabelin huippu
- on paraabelin ja sen akselin leikkauspiste
- on piste, jossa paraabelin kulkusuunta vaihtuu
- sijaitsee johtosuoran ja polttopisteen puolivälissä
Esim. 1
Määritä paraabelin yhtälö, kun sen johtosuora on \(x=-2\) ja polttopiste \((1,-3)\).
Koska johtosuora on pystysuora, paraabeli aukeaa vaakasuuntaan.
Merkitään paraabelin pistettä \((x,y)\).
Paraabelin pisteen \((x,y)\) etäisyys johtosuorasta (vaakasuora etäisyys):
\(d_1=\left|x-(-2)\right|=\left|x+2\right|.\)
Paraabelin pisteen \((x,y)\) etäisyys polttopisteestä:
\( \begin{align} d_2&=\sqrt{(x-1)^{2}+(y-(-3))^{2}}\\ &=\sqrt{(x-1)^{2}+(y+3)^{2}} \end{align} \)
Paraabelin määritelmän perusteella saadaan yhtälö:
\( \begin{align} d_1&=d_2\\ \left|x+2\right|&=\sqrt{(x-1)^{2}+(y+3)^{2}} \quad \mid \text{CAS-laskin}\\ x&=\frac{1}{6}y^{2}+y+1 \end{align} \)
Vastaus: \(\displaystyle{x=\frac{1}{6}y^{2}+y+1}\)
4.2 Paraabelin yhtälön normaalimuoto
Paraabelin yhtälön normaalimuoto (eli yleinen muoto)
Pystysuuntaan aukeava paraabeli:
$$y=ax^{2}+bx+c.$$
Vaakasuuntaan aukeava paraabeli:
$$x=ay^{2}+by+c.$$
Yhtälöissä \(a\), \(b\) ja \(c\) ovat vakioita ja \(a\neq 0\).
- Jos \(a>0\), paraabeli aukeaa ylös tai oikealle.
- Jos \(a<0\), paraabeli aukeaa alas tai vasemmalle.
Esim. 1
Määritä pystysuuntaan aukeavan paraabelin yhtälö, kun paraabeli kulkee pisteiden \((3,2)\), \((-4,-1)\) ja \((4,3)\) kautta.
Koska paraabeli aukeaa pystysuuntaan, sen yhtälö on muotoa:
Muodostetaan yhtälöryhmä:
\( \begin{cases} 2=a\cdot3^{2}+x\cdot3+c\\ -1=a\cdot(-4)^{2}+x\cdot(-4)+c\\ 3=a\cdot4^{2}+x\cdot4+c \end{cases} \)
Ratkaistaan CAS-laskimella.
\(a=\frac{1}{14}\), \(b=\frac{1}{2}\) ja \(c=-\frac{1}{7}\)
Sijoitetaan paraabelin yhtälöön kertoimien \(a\), \(b\) ja \(c\) paikalle:
\(\displaystyle{y=\frac{1}{14}x^{2}+\frac{1}{2}x-\frac{1}{7}}\).
Vastaus: \(\displaystyle{y=\frac{1}{14}x^{2}+\frac{1}{2}x-\frac{1}{7}}\)
4.3 Paraabelin yhtälön huippumuoto
Paraabelin yhtälön huippumuoto
Pystysuuntaan aukeava paraabeli:
$$y-y_{0}=a(x-x_{0})^{2}.$$
Vaakasuuntaan aukeava paraabeli:
$$x-x_{0}=a(y-y_{0})^{2}.$$
Yhtälöissä \((x_{0},y_{0})\) on paraabelin huippu ja \(a\neq 0\).
Esim. 1
Määritä vaakasuuntaan aukeavan paraabelin yhtälö, kun sen huippu on pisteessä \((-1,2)\) ja se kulkee pisteen \((0,4)\) kautta.
Vastaus: \(x=\frac{1}{4}y^{2}-y\).
Esim. 2
Saata paraabelin \(y=x^2+2x-4\) yhtälö huippumuotoon. Mitkä ovat huipun koordinaatit?
Vastaus: \(y+5=(x+1)^{2}\) ja \((-1,-5)\).
5 VEKTORI
5.1 Vektorin käsite
Vektori on matemaattinen objekti, jolla on suuruuden lisäksi suunta, mutta ei paikkaa.
Esim. 1
Idästä tuulee 4 m/s.
Merkintöjä
$$\begin{array}{cl} \bar{a}&\text{vektori}\ \bar{a}\\ -\bar{a}&\text{vektorin}\ \bar{a}\ \text{vastavektori}\\ \left|\bar{a}\right|&\text{vektorin}\ \bar{a}\ \text{itseisarvo eli pituus}\\ \bar{a}\parallel\bar{b}&\text{vektorit}\ \bar{a}\ \text{ja}\ \bar{b}\ \text{ovat}\ yhdensuuntaiset\\ \bar{a}\uparrow\uparrow\bar{b}&\text{vektorit}\ \bar{a}\ \text{ja}\ \bar{b}\ \text{ovat}\ samansuuntaiset\\ \bar{a}\uparrow\downarrow\bar{b}&\text{vektorit}\ \bar{a}\ \text{ja}\ \bar{b}\ \text{ovat}\ vastakkaissuuntaiset\\ \bar{a}\nparallel\bar{b}&\text{vektorit}\ \bar{a}\ \text{ja}\ \bar{b}\ \text{ovat}\ erisuuntaiset\\ \end{array}$$
Esim. 2
Vastaa kuvan perusteella.
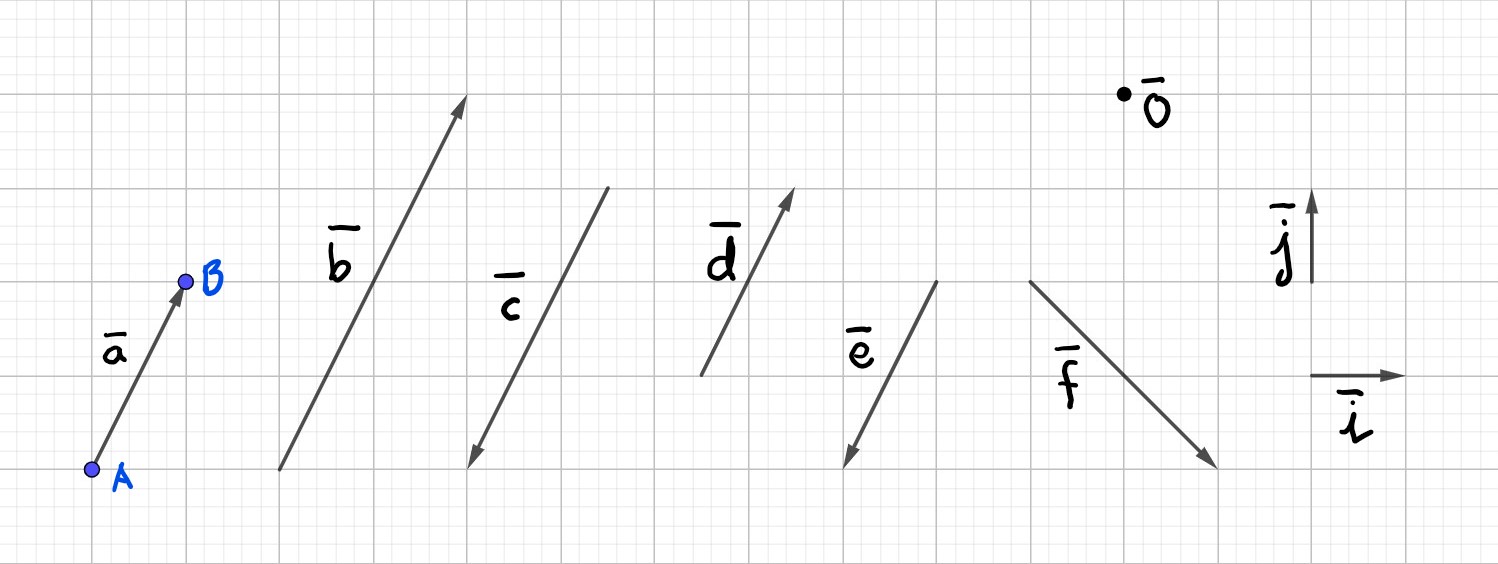
Annan esimerkki kahdesta vektorista, jotka ovat keskenään
a) yhdensuuntaisia
b) samansuuntaisia
c) vastakkaissuuntaisia
d) samat
e) vastavektoreita
f) erisuuntaisia?
a) \(\bar{a}\parallel\bar{b}\), \(\bar{b}\parallel\bar{c}\) tai \(\bar{a}\parallel\bar{c}\) (nuolien varret yhdensuuntaiset)
b) \(\bar{a}\uparrow\uparrow\bar{b}\) (nuolien kärjet osoittavat samaan suuntaan)
c) \(\bar{a}\uparrow\downarrow\bar{c}\) (nuolien kärjet osoittavat vastakkaisiin suuntiin)
d) \(\bar{a}=\bar{d}\) (nuolien kärjet osoittavat samaan suuntaan ja nuolien varret ovat yhtä pitkät)
e) \(\bar{a}=-\bar{e}\) tai \(\bar{e}=-\bar{a}\) (nuolien kärjet osoittavat vastakkaisiin suuntiin ja nuolien varret ovat yhtä pitkät)
f) \(\bar{a}\nparallel\bar{c}\)
Määritelmiä
Vektori, jonka pituus on 1, on yksikkövektori.
Vektori, jonka pituus on 0, on nollavektori.
Merkintöjä
$$\begin{array}{cl} \bar{a}^0&\text{vektorin}\ \bar{a}\ \text{suuntainen yksikkövektori}\\ \bar{i}&x\text{-akselin suuntainen yksikkövektori}\\ \bar{j}&y\text{-akselin suuntainen yksikkövektori}\\ \bar{0}&\text{nollavektori} \end{array}$$
Huom.
Nollavektorilla ei ole suuntaa. Kuvassa nollavektori voidaan esittää pisteenä.
Määritelmä
Jana, jolle on määritelty suunta alkupisteestä \(A\) loppupisteeseen \(B\), on suuntajana.
Huom.
Vektori ja suuntajana eivät ole sama asia, mutta ne voidaan rinnastaa \(\bar{a}=\overline{AB}\).
5.2 Vektorien välinen kulma
Vektorien välinen kulma tarkoittaa korkeintaan 180 asteen kulmaa, joka syntyy, kun vektorit asetetaan alkamaan samasta pisteestä.
Merkintä
Vektorien \(\bar{a}\) ja \(\bar{b}\) välinen kulma merkitään: \(\sphericalangle(\bar{a},\bar{b})\).
Esim. 1
Määritä vektorien välinen kulma.
a) \(\sphericalangle(\bar{a},\bar{b})\) b) \(\sphericalangle(\bar{c},\bar{d})\) c) \(\sphericalangle(\bar{e},\bar{f})\)
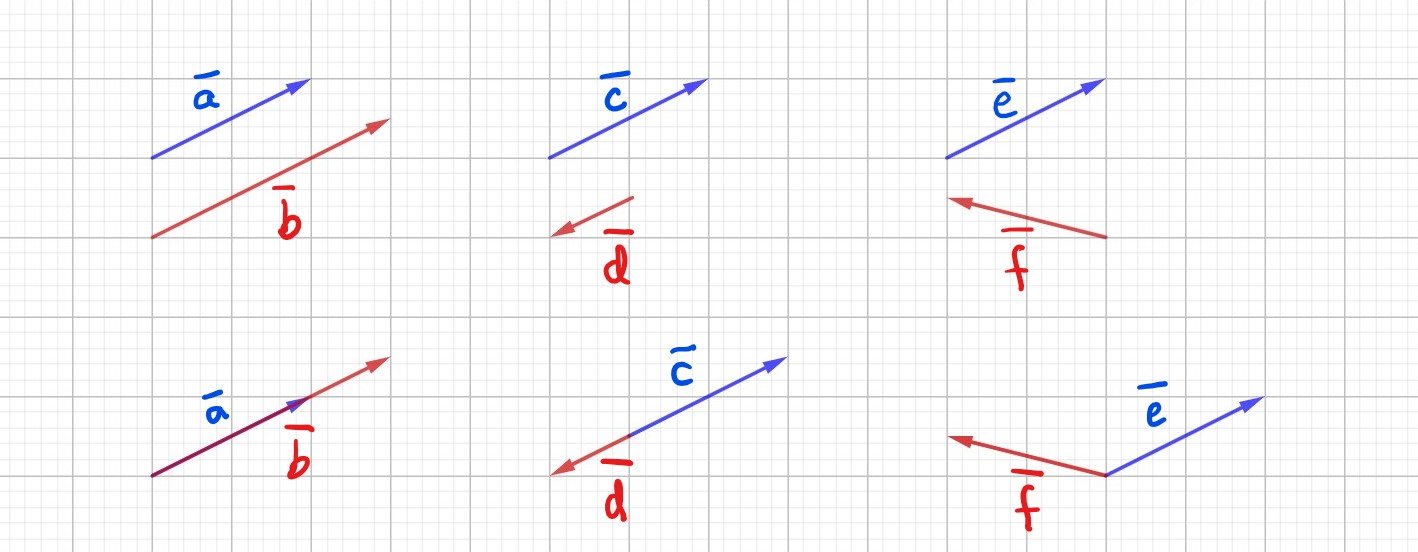
Vastaus: a) \(\sphericalangle(\bar{a},\bar{b})=0^{\circ}\) b) \(\sphericalangle(\bar{c},\bar{d})=180^{\circ}\) c) \(\sphericalangle(\bar{e},\bar{f})=139^{\circ}\)
5.3 Vektorien summa ja erotus
Vektorien summa ja erotus
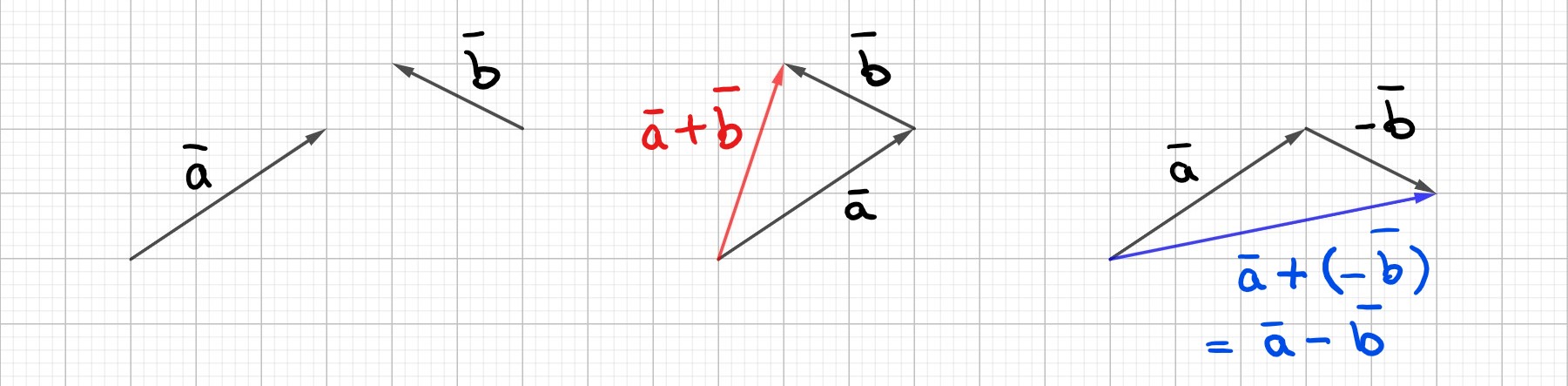
Vektorien summa
Vektorien \(\bar{a}\) ja \(\bar{b}\) summa tarkoittaa vektoria \(\bar{a}+\bar{b}\), joka saadaan asettamalla vektorit peräkkäin ja piirtämällä summavektori ensimmäisen vektorin alkupisteestä jälkimmäisen loppupisteeseen.
Vektorien erotus
Vektorien \(\bar{a}\) ja \(\bar{b}\) erotus voidaan määritellä vektorien summan ja vastavektorin avulla $$\bar{a}-\bar{b}=\bar{a}+(-\bar{b})$$ (eli vektorin vähentäminen on vastavektorin lisäämistä).
Vektorien summan ja erotuksen ominaisuuksia
1) Yhteenlaskun vaihdannaisuus:
$$\bar{a}+\bar{b}=\bar{b}+\bar{a}.$$
2) Yhteenlaskun liitännäisyys:
$$(\bar{a}+\bar{b})+\bar{c}=\bar{a}+(\bar{b}+\bar{c}).$$
3) Vastavektori:
$$\bar{a}+(-\bar{a})=\bar{a}-\bar{a}=\bar{0}.$$
4) Nollavektori:
$$\bar{a}+\bar{0}=\bar{a}.$$
5.4 Reaaliluvun ja vektorin tulo
Reaaliluvun ja vektorin tulo
Reaaliluvun \(t\) ja vektorin \(\bar{a}\) tulo tarkoittaa tulovektoria \(t\bar{a}\).
- Tulovektorin \(t\bar{a}\) pituus on \(\left|t\bar{a}\right|=\left|t\right|\left|\bar{a}\right|\)
- Jos \(t>0\) ja \(\bar{a}\neq\bar{0}\), \(t\bar{a}\uparrow\uparrow\bar{a}\).
- Jos \(t<0\) ja \(\bar{a}\neq\bar{0}\), \(t\bar{a}\uparrow\downarrow\bar{a}\).
- Jos \(t=0\) ja \(\bar{a}\neq\bar{0}\), \(t\bar{a}=0\cdot\bar{a}=\bar{0}\).
- Jos \(t\in\mathbb{R}\) ja \(\bar{a}=\bar{0}\), \(t\bar{a}=t\cdot\bar{0}=\bar{0}\).
Esim. 1
Olkoon vektorin \(\bar{a}\) pituus \(3\) ja suunta \(x\)-akselin positiiviseen suuntaan. Piirrä vektorit.
a) \(2\bar{a}\)
b) \(\frac{1}{3}\bar{a}\)
c) \(-\frac{2}{3}\bar{a}\)
d) \(0\bar{a}\)
Reaaliluvun ja vektorin tulon ominaisuuksia
1) Reaaliluvun ja vektorin tulon vaihdannaisuus:
$$t\bar{a}=\bar{a}t.$$
2) Reaaliluvun ja vektorin tulon liitännäisyys:
$$(st)\bar{a}=s(t\bar{a})=st\bar{a}.$$
3) Reaalilukujen summan ja vektorin tulon osittelu:
$$(s+t)\bar{a}=s\bar{a}+t\bar{a}.$$
4) Reaaliluvun ja vektorien summan tulon osittelu:
$$t(\bar{a}+\bar{b})=t\bar{a}+t\bar{b}.$$
Esim. 2
Vektoreille \(\bar{a}\) ja \(\bar{b}\), jotka eivät ole nollavektoreita, on voimassa yhtälö \(2(\bar{a}-\bar{b})=4\bar{a}-\bar{b}\).
a) Osoita, että vektorit \(\bar{a}\) ja \(\bar{b}\) ovat vastakkaissuuntaisia.
b) Vertaa vektorin \(\bar{a}\) pituutta vektorin \(\bar{b}\) pituuteen.
6 VEKTORI KOORDINAATISTOSSA
6.1 Vektori xy-koordinaatistossa
Merkintä
Yksikkövektoria, joka osoittaa
- x-akselin positiiviseen suuntaan merkitään \(\bar{i}\).
- y-akselin positiiviseen suuntaan merkitään \(\bar{j}\).
Esim. 1
Esitä vektori \(\bar{a}\) xy-koordinaatiston kantavektorien \(\bar{i}\) ja \(\bar{j}\) avulla.
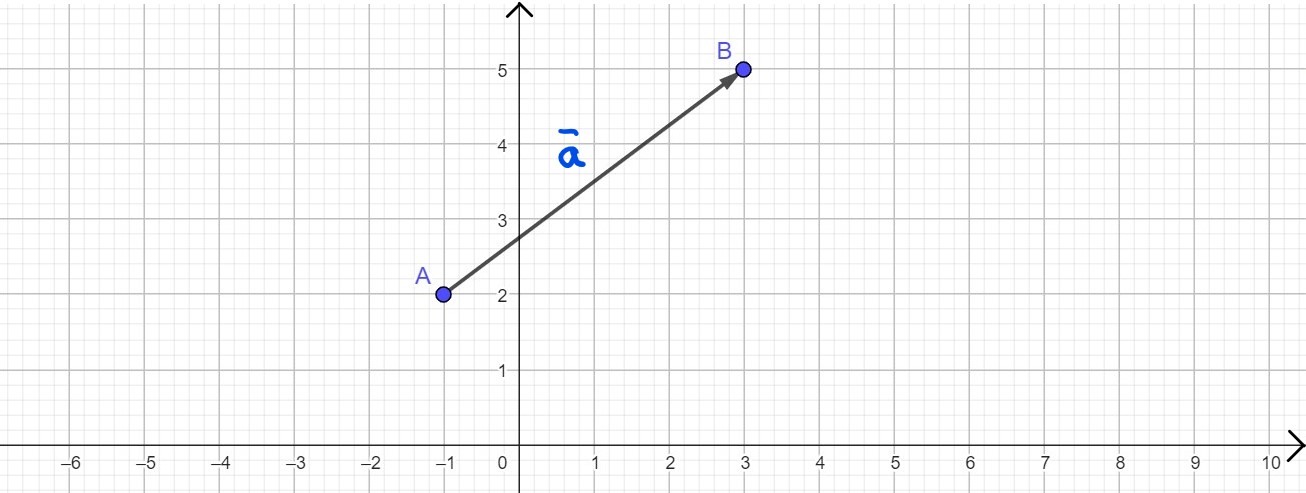
Vastaus: \(\bar{a}=4\bar{i}+3\bar{j}\)
6.2 Paikkavektori
Paikkavektori
Pisteen \(P(x,y)\) paikkavektori on $$\overline{OP}=x\bar{i}+y\bar{j}.$$
Esim. 1
Määritä pisteen \(P(3,-4)\) paikkavektori.
Vastaus: \(\overline{OP}=3\bar{i}-4\bar{j}\).
Esim. 2
Pisteestä \(A=(2,-3)\) siirrytään vektorin \(\bar{a}=5\bar{i}+4\bar{j}\) verran pisteeseen \(B\). Mitkä ovat pisteen \(B\) koordinaatit?
Vastaus: \(B=(7,1)\).
Huom.
GeoGebralla erimerkiksi vektori \(\bar{a}=5\bar{i}+4\bar{j}\) voidaan määrittää komennolla Vektori((5,4)). Vektoreiden yhteen- ja vähennyslaskua sekä reaaliluvulla kertomista voidaan suorittaa GeoGebralla käyttäen kyseistä komentoa ja laskutoimitusmerkkejä.
6.3 Pisteiden välinen vektori
Pisteiden \(A\) ja \(B\) välinen vektori
$$\overline{AB}=(b_x-a_x)\bar{i}+(b_y-a_y)\bar{j},$$
missä \((a_x,a_y)\) on pisteen \(A\) ja \((b_x,b_y)\) pisteen \(B\) koordinaatit.
Esim. 1
Olkoon pisteet \(A(1,2)\) ja \(B(6,5)\). Määritä pisteiden \(A\) ja \(B\) välinen vektori.
Vastaus: \(\overline{AB}=5\bar{i}+3\bar{j}\).
6.4 Vektorin pituus
Vektorin pituus
Olkoon vektori \(\bar{a}=a_{x}\bar{i}+a_{y}\bar{j}\). Tällöin vektorin \(\bar{a}\) pituus on $$\left|\bar{a}\right|=\sqrt{a_{x}^{2}+a_{y}^{2}}.$$
Esim. 1
Laske vektorin pituus.
a) \(\bar{a}=3\bar{i}+4\bar{j}\)
b) \(\bar{b}=8\bar{i}-6\bar{j}\)
Vastaus: a) \(\left|\bar{a}\right|=5\) \(\left|\bar{b}\right|=10\)
Pisteiden \(A\) ja \(B\) välisen vektorin pituus
Pisteiden \(A\) ja \(B\) välisen vektorin \(\overline{AB}\) pituus on pisteiden \(A\) ja \(B\) välinen etäisyys:
$$\left|\overline{AB}\right|=\sqrt{(b_x-a_x)^2+(b_y-a_y)^2},$$
missä \((a_x,a_y)\) on alkupisteen \(A\) ja \((b_x,b_y)\) loppupisteen \(B\) koordinaatit.
Esim. 2
Olkoon pisteet \(A(1,2)\) ja \(B(6,5)\). Määritä pisteiden \(A\) ja \(B\) välisen vektorin pituus.
Vastaus: \(\left|\overline{AB}\right|=\sqrt{34}\).
6.5 Vektorin komponentit
Esim.
Vektorin \(\bar{a}\) pituus on \(\left|\bar{a}\right|=6{,}0\) ja suuntakulma \(\alpha=30^{\circ}\). Määritä laskemalla kantavektorien \(\bar{i}\) ja \(\bar{j}\) suuntaiset komponentit \(\bar{a}_{x}\) ja \(\bar{a}_{y}\).
Vastaus: \(\bar{a}_{x}\approx5{,}2\bar{i}\) ja \(\bar{a}_{y}=3\bar{j}\).
Esim.
Auto on pysäköity mäkeen, jonka kaltevuus on \(15^{\circ}\). Maa vetää autoa puoleensa \(6000\ N\) voimalla. Määritä laskemalla maan vetovoiman mäen pinnan suuntaisen ja pintaa vastaan kohtisuoran komponentin suuruus.
Vastaus: Mäen pinnan suuntaisen komponentin suuruus on \(\left|\overline{G}_{x}\right|\approx1600\ N\) ja mäen pintaa vastaan kohtisuoran \(\left|\overline{G}_{y}\right|\approx5800\ N\).
6.6 Yksikkövektori
Yksikkövektori
Vektorin \(\bar{a}\) suuntainen yksikkövektori on $$\bar{a}^{0}=\frac{1}{\left|\bar{a}\right|}\bar{a}=\frac{\bar{a}}{\left|\bar{a}\right|}.$$
Esim. 1
Määritä vektorin \(\bar{a}=4\bar{i}+3\bar{j}\)
a) suuntainen yksikkövektori
b) kanssa vastakkaissuuntainen vektori \(\bar{b}\), jonka pituus on \(2\).
Vastaus:a) \(\bar{a}^{0}=\frac{4}{5}\bar{i}+\frac{3}{5}\bar{j}\) b) \(\bar{b}=-2\bar{a}^{0}=-\frac{8}{5}\bar{i}-\frac{6}{5}\bar{j}\).
Esim. 2
Pisteestä \(P(-7,6)\) siirrytään \(10\) yksikköä vektorin \(\bar{a}=3\bar{i}-4\bar{j}\) suuntaan. Mihin pisteeseen \(A\) päädytään?
Vastaus: \((-1,-2)\).
Huom.
GeoGebralla vaikkapa vektorin \(\bar{a}=3\bar{i}-4\bar{j}\) suuntainen yksikkövektori voidaan määrittää komennolla yksikkövektori((3,-4)).
6.7 Yhdensuuntaiset vektorit
Vektorien yhdensuuntaisuus
Vektorit \(\bar{a}\) ja \(\bar{b}\) ovat yhdensuuntaiset, jos ja vain jos vektori \(\bar{a}\) saadaan vektorista \(\bar{b}\) kertomalla nollasta eroavalla reaaliluvulla \(t\) eli $$\bar{a}\parallel\bar{b}\quad\Leftrightarrow\quad\bar{a}=t\bar{b}, t\neq0.$$
Esim. 1
Ovatko vektorit \(\bar{a}=2\bar{i}-4\bar{j}\) ja \(\bar{b}=-3\bar{i}+6\bar{j}\) yhdensuuntaiset?
Vastaus: Kyllä, koska on olemassa \(t=-\frac{2}{3}\), jolle pätee \(\bar{a}=-\frac{2}{3}\bar{b}\).
Huom.
GeoGebralla vaikkapa reaaliluvun \(-2\) ja vektorin \(3\bar{i}-4\bar{j}\) tulo lasketaan \(-2\cdot(3,-4)\).
6.8 Pistetulo
Vektorien pistetulo (eli skalaaritulo)
Vektorien \(\bar{a}=a_{x}\bar{i}+a_{y}\bar{j}\) ja \(\bar{b}=b_{x}\bar{i}+b_{y}\bar{j}\) pistetulo lasketaan
$$\bar{a}\cdot \bar{b}=a_{x}b_{x}+a_{y}b_{y}.$$
Esim. 1
Laske vektorien \(\bar{a}=2\bar{i}-4\bar{j}\) ja \(\bar{b}=-3\bar{i}+5\bar{j}\) pistetulo.
Vastaus: \(-26\).
Vektorien kohtisuoruusehto
Vektorit \(\bar{a}\) ja \(\bar{b}\), jotka eivät ole nollavektoreita, ovat kohtisuorassa toisiaan vastaan, jos ja vain jos niiden pistetulo \(\bar{a}\cdot \bar{b}\) on nolla eli
$$\bar{a}\perp \bar{b}\quad \Leftrightarrow \quad \bar{a}\cdot \bar{b}=0 \quad (\bar{a}\neq\bar{0}, \bar{b}\neq\bar{0}).$$
Esim. 2
Tutki, ovatko vektorit \(\bar{a}=2\bar{i}-3\bar{j}\) ja \(\bar{b}=6\bar{i}+4\bar{j}\) kohtisuorassa toisiaan vastaan.
Vastaus: Kyllä, koska pistetulo on nolla.
Vektorien pistetulon ominaisuuksia
1) Pistetulon vaihdannaisuus
$$\bar{a}\cdot \bar{b}=\bar{b}\cdot \bar{a}$$
2) Osittelu
$$\bar{a}\cdot(\bar{b}+\bar{c})=\bar{a}\cdot \bar{b}+\bar{a}\cdot \bar{c}$$
3) Kertoimen siirtosääntö
$$(s\bar{a})\cdot (t\bar{b})=(st)\bar{a}\cdot \bar{b}$$
4) Vektorin pistetulo itsensä kanssa
$$\bar{a}\cdot \bar{a}=\left|\bar{a}\right|^{2}$$
6.9 Pistetulo ja vektorien välinen kulma
Vektorien välisen kulman laskeminen
Olkoon vektorit \(\bar{a}\) ja \(\bar{b}\), jotka eivät ole nollavektoreita. Tällöin vektorien \(\bar{a}\) ja \(\bar{b}\) välinen kulma voidaan ratkaista yhtälöstä
$$\cos \left(\bar{a}, \bar{b}\right)=\frac{\bar{a}\cdot \bar{b}}{\left|\bar{a}\right|\left|\bar{b}\right|},$$ missä \(\cos \left(\bar{a}, \bar{b}\right)=\cos \left(\sphericalangle \left(\bar{a}, \bar{b}\right)\right)\).
Esim. 1
Laske vektorien \(\bar{a}=4\bar{i}-2\bar{j}\) ja \(\bar{b}=6\bar{i}+3\bar{j}\) välinen kulma.
Vastaus: \(\sphericalangle \left(\bar{a}, \bar{b}\right)\approx53{,}1^{\circ}\).
7 GEOMETRIAA VEKTOREILLA
7.1 Suuntavektori
Suoran suuntavektoreita ovat kaikki vektorit, jotka ovat suoran kanssa yhdensuuntaisia.
Lause
Olkoon \(s_{x}\neq0\) ja \(\bar{s}=s_{x}\bar{i}+s_{y}\bar{j}\) suoran eräs suuntavektori. Tällöin suoran kulmakerroin on \(k=\frac{s_{y}}{s_{x}}\).
Lause
Olkoon suoran kulmakerroin \(k\). Tällöin suoran eräs suuntavektori on \(\bar{s}=\bar{i}+k\bar{j}\).
Esim. 1
Määritä suorien \(y=5x+4\) ja \(y=\frac{2}{3}x-1\) välinen kulma suuntavektorien avulla.
Vastaus: \(45^{\circ}\).
7.2 Normaalivektori
Suoran normaalivektoreita ovat kaikki vektorit, jotka ovat suoraa vastaan kohtisuorassa.
Lause
Olkoon \(a\neq0\) ja \(b\neq0\) ja \(ax+by+c=0\) suoran yhtälö normaalimuodossa. Tällöin suoran eräs normaalivektori on \(\bar{n}=a\bar{i}+b\bar{j}\).
Esim. 1
Määritä suorien \(y=5x+4\) ja \(y=\frac{2}{3}x-1\) välinen kulma normaalivektorien avulla.
Vastaus: \(45^{\circ}\).
Esim. 2
Määritä laskemalla suoralta \(y=2x+3\) piste \(B\), joka on lähinnä pistettä \(A(5,-2)\).
Vastaus: \((-1,1)\)
7.3 Todistamista
Todistetaan seuraava tasogeometriaan liittyvä lause vektorien avulla:
Lause
Neliön lävistäjät ovat kohtisuorassa toisiaan vastaan.
TODISTUS:
Olkoon neliön sivun pituus \(a\). Sovitetaan neliö xy-koordinaatiston ensimmäiseen neljännekseen siten, että yksi kärki on origossa ja kaksi sivua ovat koordinaattiakseleiden päällä.
Merkitään koordinaattiakseleiden päällä olevia sivuja vektoreina \(a\bar{i}\) ja \(a\bar{j}\).
Tällöin lävistäjät voidaan ilmoittaa vektoreina \(\bar{c}=a\bar{i}+a\bar{j}\) ja \(\bar{d}=-a\bar{i}+a\bar{j}\).
Lävistäjät \(\bar{c}\) ja \(\bar{d}\) ovat kohtisuorassa toisiaan vastaan, jos niiden pistetulo on nolla.
$$\bar{c}\cdot \bar{d}=a\cdot (-a)+a\cdot a=-a^{2}+a^{2}=0$$
Koska pistetulo on nolla, neliön lävistäjät ovat kohtisuorassa toisiaan vastaan. \(_\square\)