Funktiot ja yhtälöt 2 (MAA5)
Laajuus
2 op
Yleiset tavoitteet (LOPS 2021)
Moduulin tavoitteena on, että opiskelija
- tutustuu ilmiöiden matemaattiseen mallintamiseen sini- ja kosinifunktioiden sekä eksponentti- ja logaritmifunktioiden avulla
- tutkii sini- ja kosinifunktioita yksikköympyrän symmetrioiden avulla
- osaa ratkaista sellaisia trigonometrisia yhtälöitä, jotka ovat tyyppiä \(\sin f(x)=a\) tai \(\sin f(x)=\sin g(x)\)
- osaa soveltaa sini- ja kosinifunktioiden yhteyttä \(\sin^{2}x+\cos^{2}x=1\)
- tuntee eksponentti- ja logaritmifunktioiden ominaisuudet ja osaa ratkaista niihin liittyviä yhtälöitä
- osaa käyttää ohjelmistoja funktioiden tutkimisessa, yhtälöiden ratkaisemisessa ja sovellusten yhteydessä.
Keskeiset sisällöt (LOPS 2021)
- suunnattu kulma ja radiaani
- yksikköympyrä
- sini- ja kosinifunktiot symmetria- ja jaksollisuusominaisuuksineen
- sini- ja kosiniyhtälöiden ratkaiseminen
- murtopotenssi ja sen yhteys juureen
- eksponenttifunktiot ja -yhtälöt
- logaritmi ja logaritmin laskusäännöt
- logaritmifunktiot ja yhtälöt
Aikataulu
Suoritus
- osallistuminen
- tehtävien tekeminen
- monivalintatehtävien tekeminen
- loppukoe
Arviointi
- säännöllinen, aktiivinen ja vastuullinen osallistuminen +1 p
- tehtävien asianmukainen ja jatkuva tekeminen +1 p
- monivalintatehtävistä +1 p kustakin tehdystä monivalintakokonaisuudesta, saavutettava tavoitetaso 80 %, yht. max. 5 p
- loppukokeesta max. 55 p
- max. 60 p (teoreettisesti 62 p)
- 30 % arviointi
| Pisteet | Arvosana | Muuta |
|---|---|---|
| 0 - 9 | i \(\rightarrow\) K | Pakko täydentää. |
| 10 - 17 | i \(\rightarrow\) 4 | Oikeus täydentää. |
| 18 - 25 | 5 | |
| 26 - 33 | 6 | |
| 34 - 41 | 7 | |
| 42 - 49 | 8 | |
| 50 - 57 | 9 | |
| 58 - 60 | 10 |
Keskeyttäminen
Opettaja keskeyttää opiskelijan opintojakson, jos
- opiskelija niin pyytää
- opiskelija ei ole läsnä opintojakson kahdella ensimmäisellä opetuskerralla ja opiskelija ei ole yhteydessä opettajaan eikä opettaja saa yhteyttä opiskelijaan.
Opettaja voi keskeyttää opiskelijan opintojakson, jos opiskelijalla on viisi poissaoloa. Tällaiset tilanteet opettaja käy läpi tapauskohtaisesti ja on ennen lopullista keskeytystä yhteydessä opiskelijaan.
Keskeyttämisestä opettaja merkitsee opintojaksosta opiskelijalle K-merkinnän Wilmaan ja poistaa opiskelijan sen jälkeen Wilman ryhmästä. Opettaja lähettää keskeyttämisestä viestin opiskelijalle, alaikäisen opiskelijan huoltajalle, ryhmänohjaajalle ja opolle.
1 PERUSKÄSITTEITÄ
1.1 Suunnattu kulma
Kulma on kahden samasta pisteestä alkavan puolisuoran väliin jäävä aukeama. Puolisuoria kutsutaan kulman kyljiksi.
Suunnattu kulma: Jos nollakulmasta alkaen kulman toista kylkeä kierretään vastapäivään, on kulma positiivinen. Jos kierto tapahtuu myötäpäivään, on kulma negatiivinen.
1.2 Radiaani
Määritelmä
Kulman suuruus radiaaneina on kulmaa vastaavan kaaren pituuden ja säteen suhde.
$$\alpha=\frac{b}{r}$$
Esim.
Kulmaa vastaavan kaaren pituus on 2,0 cm ja säde 3,0 cm. Määritä kulman suuruus radiaaneina.
Huom.
Jos kulmaa vastaavan kaaren pituus on yhtä suuri kuin säde, niin kulman suuruus on 1 (rad).
1.3 Radiaanit ja asteet
Puoliympyrän muotoisen sektorin keskuskulman suuruus on asteina 180° ja radiaaneina
$$\alpha=\frac{b}{r}=\frac{\pi \cancel{r}}{\cancel{r}}=\pi.$$
Siis asteiden ja radiaanien välinen yhteys on: $$180^{\circ} = \pi.$$
Esim. 1
Muuta 54° radiaaneiksi.
Esim. 2
Muuta 0,312 (rad) asteiksi.
2 TRIGONOMETRIA
2.1 Yksikköympyrä
Yksikköympyrän keskipiste on asetettu koordinaatiston origoon ja säde on 1. Yksikköympyrätarkastelussa suunnatun kulman alkukylki on positiivisella x-akselilla ja loppukyljen päätepistettä ympyrän kehällä kutsutaan kehäpisteeksi.
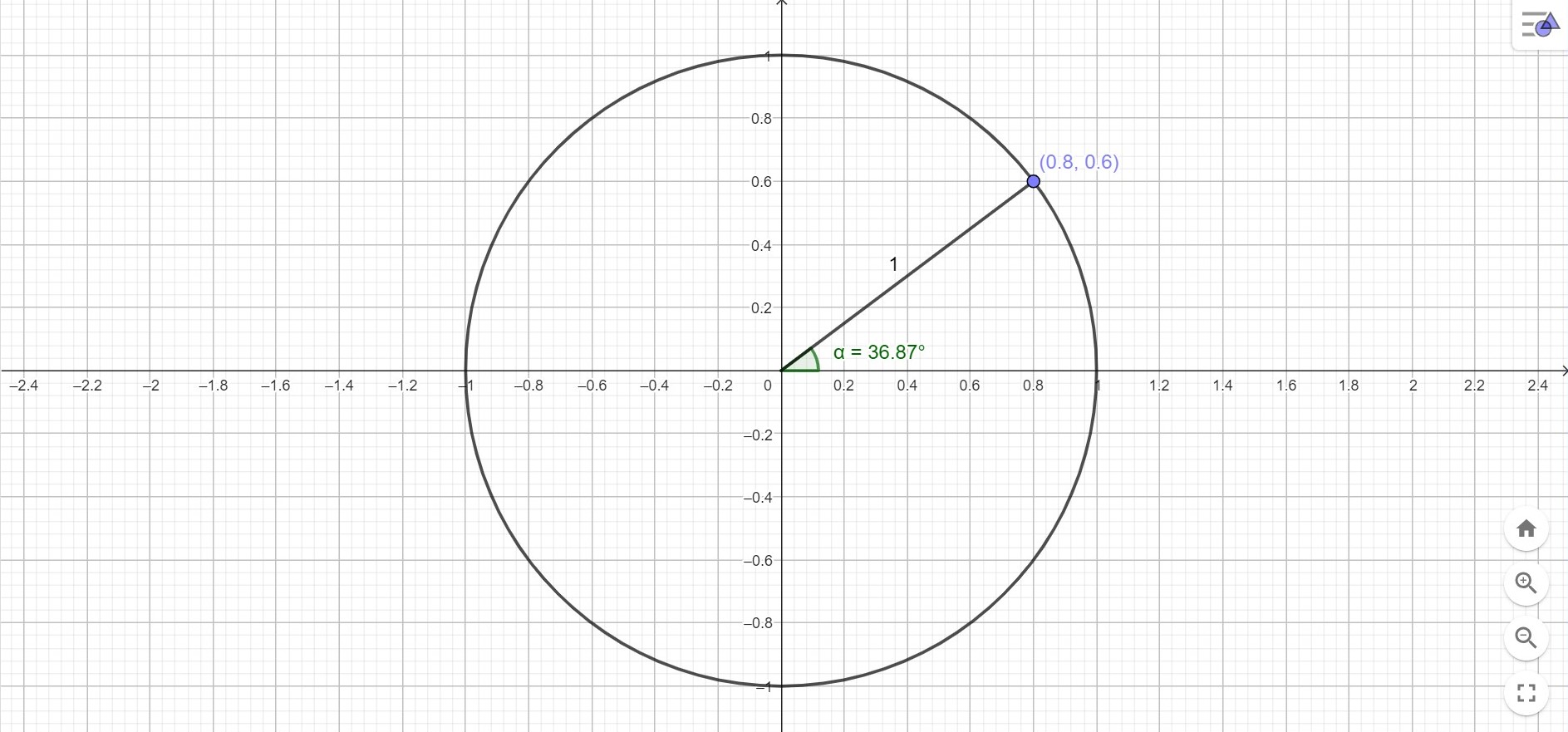
Kehäpisteen x-koordinaatti on vastaa keskuskulman kosinia ja y-koordinaatti siniä.
Kulman sinin ja kosinin määritelmä
Olkoon suunnattu kulma \(\alpha\) ja sen kehäpisteen koordinaatit \(\left(x,y\right)\). Tällöin pätee
\(\cos \alpha =\frac{x}{1}=x\)
ja
\(\sin \alpha =\frac{y}{1}=y\).
Sinin ja kosinin arvot ovat välillä \(\left[-1,1\right]\). Toisin sanoen kaikilla kulman \(\alpha\) arvoilla pätee $$-1 \leq \sin\alpha \leq 1 \quad\quad \text{ja} \quad\quad -1 \leq \cos\alpha \leq 1.$$
Kehäpisteen y-koordinaatin suhde x-koordinaattiin vastaa keskuskulman tangenttia.
Kulman tangentin määritelmä
Olkoon suunnattu kulma \(\alpha\) ja sen kehäpisteen koordinaatit \(\left(x,y\right)\). Tällöin pätee
\(\tan \alpha =\frac{y}{x}=\frac{\sin\alpha}{\cos\alpha}\),
missä \(x=\cos \alpha \neq 0\) eli \(\alpha\neq\frac{\pi}{2}+n\cdot\pi\), \(n\in\mathbb{Z}\).
Huom.
Kulmien sinin, kosinin ja tangentin arvojen etumerkki voidaan päätellä koordinaatiston neljänneksestä, jossa kulman kehäpiste sijaitsee.

2.2 Tarkkoja arvoja
Kulmille \(0\), \(\frac{\pi}{2}\), \(-\frac{\pi}{2}\) ja \(\pi\) (asteina 0°, 90°, -90° ja 180°) on helppo määrittää tarkat sinin ja kosinin arvot yksikköympyrän avulla.
$$ \begin{array}{lll} \hline \mathbf{kulma} & \mathbf{sini} & \mathbf{kosini}\\ \hline \ \ \ ~0 & \sin 0=0 & \cos 0=1\\ \ \ \ \frac{\pi}{2} & \sin \frac{\pi}{2}=1 & \cos \frac{\pi}{2}=0\\ -\frac{\pi}{2} & \sin \left(-\frac{\pi}{2}\right)=-1 & \cos \left(-\frac{\pi}{2}\right)=0\\ \ \ \ ~\pi & \sin \pi=0 & \cos \pi =-1\\ \hline \end{array} $$
Lisäksi tietyille muillekin kulmille voidaan määrittää tarkat arvot niin sanottujen muistikolmioiden avulla. Nämä löytyvät taulukkokirjasta.
2.3 Jaksollisuus
Yksikköympyrässä suunnatun kulman kehäpiste saa uudelleen samat koordinaattien arvot, kun loppukylki kiertää täyden kierroksen vasta- tai myötäpäivään.
Sinin ja kosinin jaksollisuus
Kun kulmaan \(\alpha\) lisätään tai siitä vähennetään kulman \(2\pi\) (360°) monikerta, kulman sinin ja kosinin arvo pysyy samana:
$$\sin\alpha=\sin\left(\alpha+n\cdot 2\pi\right)$$
$$\cos\alpha=\cos\left(\alpha+n\cdot 2\pi\right),$$
missä \(n\) on kokonaisluku.
Esim.
Määritä sinin ja kosinin arvot ilman laskinta.
a) \(\sin\left(\frac{\pi}{4}-8\pi\right)\)
b) \(\cos7\pi\)
c) \(\sin 390^{\circ}\).
2.4 Palautuskaavat
Yksikköympyrän symmetriasta seuraavien palautuskaavojen avulla minkä tahansa kulman sinin ja kosinin laskeminen voidaan palauttaa välille \(\left[0,\frac{\pi}{2}\right]\) eli asteina \(\left[0^{\circ},90^{\circ}\right]\).
Kulmat \(\alpha\) ja \(-\alpha\) ovat toistensa vastakulmat.
Vastakulmien sini ja kosini
Vastakulmien
- sinit ovat toistensa vastaluvut: $$\sin \alpha =-\sin\left(-\alpha\right)$$
- kosinit ovat samat: $$\cos \alpha =\cos\left(-\alpha\right).$$
Esim. 1
Määritä ilman laskinta
a) \(\cos\left(-\frac{\pi}{3}\right)\)
b) \(-\sin\left(-\frac{\pi}{3}\right)\)
c) \(\sin\left(-\frac{\pi}{4}\right)\).
Kulmat \(\alpha\) ja \(\pi-\alpha\) ovat toistensa suplementtikulmat.
Suplementtikulmien sini ja kosini
Suplementtikulmien
- sinit ovat samat: $$\sin \alpha =\sin\left(\pi-\alpha\right)$$
- kosinit ovat toistensa vastaluvut: $$\cos \alpha =-\cos\left(\pi-\alpha\right).$$
Esim. 2
Määritä ilman laskinta
a) \(\sin\frac{2\pi}{3}\)
b) \(\cos\frac{5\pi}{6}\)
c) \(\sin\frac{4\pi}{3}\).
2.5 Sinin ja kosinin yhteys
Suorakulmaisessa kolmiossa sinin ja kosinin välillä on yhteys. Toisen terävän kulman kannalta pätee $$\sin\alpha=\frac{a}{c}$$ ja toisen $$\cos\left(\frac{\pi}{2}-\alpha\right)=\frac{a}{c}.$$
Sinin ja kosinin yhteys
$$\sin \alpha =\cos\left(\frac{\pi}{2}-\alpha\right)$$
$$\cos \alpha =\sin\left(\frac{\pi}{2}-\alpha\right).$$
2.6 Trigonometrian peruskaava
Yksikköympyrän yhtälö on \(x^2+y^2=1\). Sijoittamalla yhtälöön kehäpisteen koordinaatteina \(x=\cos\alpha\) ja \(y=\sin\alpha\) saadaan: $$ \begin{align} x^2+y^2&=1\\ \left(\cos\alpha\right)^{2}+\left(\sin\alpha\right)^{2}&=1\\ \left(\sin\alpha\right)^{2}+\left(\cos\alpha\right)^{2}&=1\\ \sin^{2}\alpha+\cos^{2}\alpha&=1. \end{align} $$
Trigonometrian peruskaava
Kulman sinin ja kosinin neliöiden summa on 1:
$$\sin^{2}\alpha+\cos^{2}\alpha=1.$$
Huom.
Laskimeen vaikkapa \(\sin^{2}\alpha\) näppäillään \(\left(\sin\left(\alpha\right)\right)^{2}\).
2.7 Kaksinkertaisen kulman sini ja kosini
Kaksinkertaisen kulman sini
$$\sin 2\alpha=2\sin\alpha\cos\alpha.$$
Kaksinkertaisen kulman kosini
$$ \begin{align} \cos 2\alpha &=\cos^{2}\alpha-\sin^{2}\alpha\\ &=2\cos^{2}\alpha-1\\ &=1-2\sin^{2}\alpha. \end{align} $$
3 TRIGONOMETRISET FUNKTIOT
3.1 Siniyhtälö
Siniyhtälö
Siniyhtälöllä \(\sin\alpha=b\) on ratkaisu, jos ja vain jos \(-1\leq b\leq 1\).
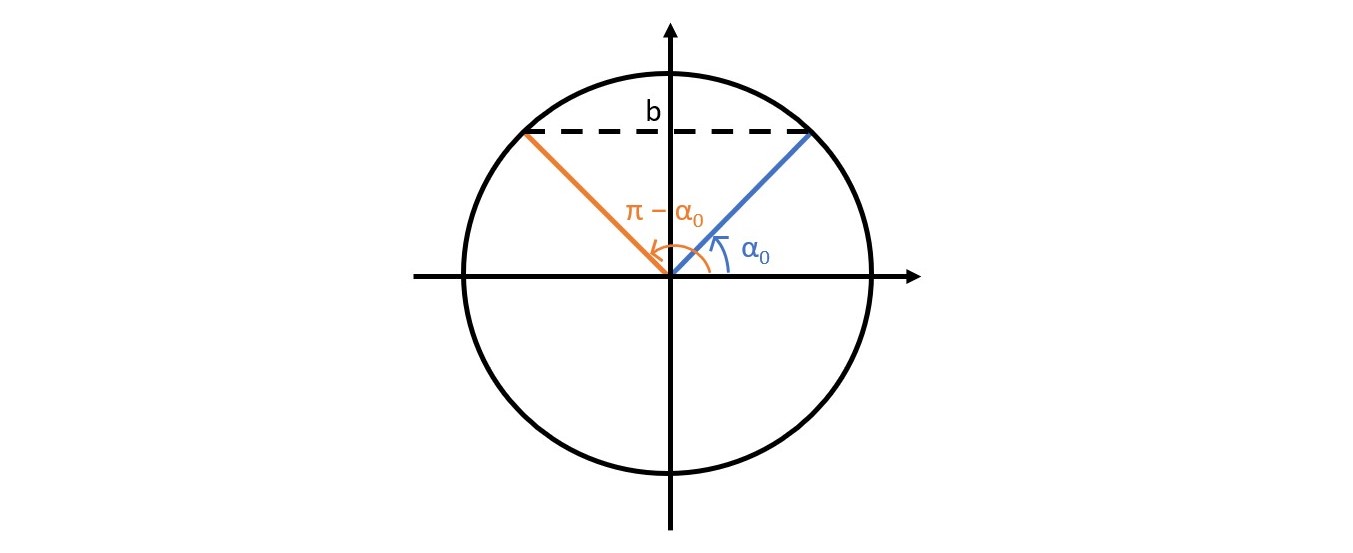
Jos \(\alpha_{0}\) on jokin kulma, joka toteuttaa yhtälön \(\sin\alpha=b\), niin yhtälön ratkaisujen joukko on $$\alpha=\alpha_{0}+n\cdot2\pi \quad \text{tai} \quad \alpha=\pi-\alpha_{0}+n\cdot2\pi,$$ missä \(n\) on kokonaisluku.
Esim. 1
Ratkaise yhtälö \(3\sin\alpha=0{,}9\).
Esim. 2
Ratkaise yhtälö \(\sin 2\alpha=\frac{\sqrt{3}}{2}\).
Esim. 3
Määritä CAS-laskimella yhtälön \(8\sin2\alpha +4=0\).
a) kaikki ratkaisut
b) ratkaisut välillä \(\left[0,\pi\right]\).
Esim. 4
Ratkaise yhtälö \(\sin 5\alpha=\sin 3\alpha\). Mitkä ratkaisuista ovat välillä \(\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\).
3.2 Kosiniyhtälö
Kosiniyhtälö
Kosiniyhtälöllä \(\cos\alpha=a\) on ratkaisu, jos ja vain jos \(-1\leq a\leq 1\).
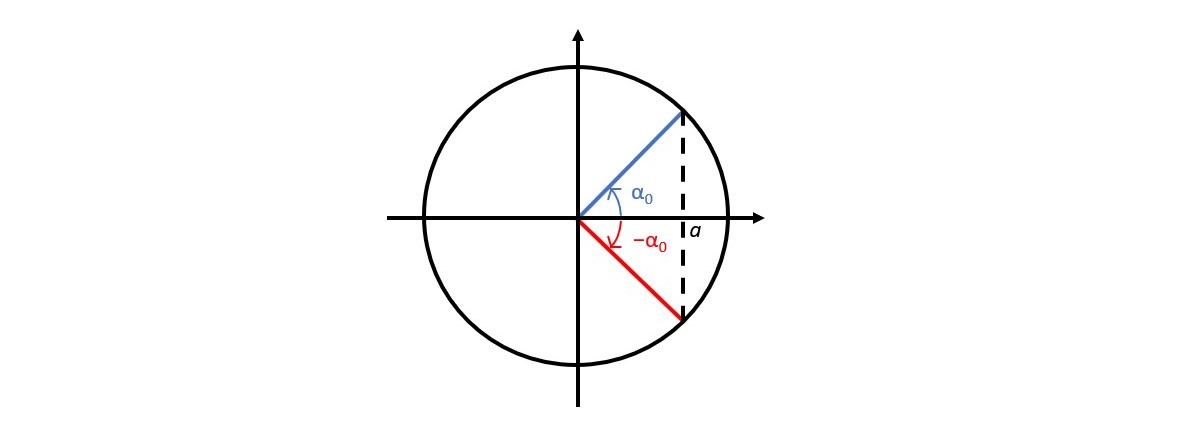
Jos \(\alpha_{0}\) on jokin kulma, joka toteuttaa yhtälön \(\cos\alpha=a\), niin yhtälön ratkaisujen joukko on $$\alpha=\alpha_{0}+n\cdot2\pi \quad \text{tai}\quad \alpha=-\alpha_{0}+n\cdot2\pi,$$ missä \(n\) on kokonaisluku.
Esim. 1
Ratkaise yhtälö \(3\cos\alpha-1=0\) kahden desimaalin tarkkuudella.
3.3 Sini- ja kosinifunktio
Määritelmä
Funktio \(f\) on jaksollinen, jos on olemassa luku \(a\neq0\), jolla \(f(x+a)=f(x)\) kaikilla \(x\).
Lukua \(a\) kutsutaan jaksoksi ja pienintä positiivista jaksoa funktion perusjaksoksi.
Sinifunktio \(\sin x\) ja kosinifunktio \(\cos x\) ovat jaksollisia funktioita, koska molempien funktioiden arvot toistuvat \(2\pi\):n mittaisten perusjaksojen välein. Kaikilla \(x\) on voimassa: $$\sin(x+2\pi)=\sin x\quad \text{ja} \quad \cos(x+2\pi)=\cos x.$$
Sini- ja kosinifunktion ominaisuuksia
- määrittelyjoukko \(\mathbb{R}\) (muuttuja voi saada minkä tahansa reaalilukuarvon = suunnatun kulman suuruus radiaaneina)
- arvojoukko \(\left[-1,1\right]\) (funktion arvot ovat välillä -1...1)
- jaksollisia, perusjaksona \(2\pi\) (funktion arvot toistuvat \(2\pi\) välein)
3.4 Kuvaajien tulkinta
Amplitudi on funktion kuvaajan suurin poikkeama kuvaajan keskilinjasta.
Funktio \(f(x)=\sin x\)
- amplitudi on \(1\)
- pienin arvo on \(-1\)
- suurin arvo on \(1\)
- perusjakso on \(2\pi\)
Funktio \(f(x)=a\sin bx+ d\), missä \(a>0\) ja \(b>0\)
- amplitudi on \(a\)
- pienin arvo on \(-a+d\)
- suurin arvo on \(a+d\)
- perusjakso on \(\frac{2\pi}{b}\)
Yleinen sinifunktio \(f(x)=a\sin (bx+c)+ d\), missä \(a>0\) ja \(b>0\)
- vakiot \(a\), \(b\) ja \(d\) vaikuttavat kuvaajaan kuten funktiolla \(f(x)=a\sin bx+ d\)
- vakio \(c\) vaikuttaa kuvaajan vaakasuuntaiseen sijaintiin
- jos \(c>0\), kuvaaja siirtyy \(c\) yksikköä vasemmalle
- jos \(c>0\), kuvaaja siirtyy \(c\) yksikköä oikealle
4 EKSPONENTTI JA LOGARITMI
4.1 Murtopotenssi
Murtopotenssi on potenssi, jonka eksponentti on murtoluku.
Yleisen juuren määritelmästä seuraa $$\left(\sqrt[n]{a}\right)^{n}=a.$$
Toisaalta voidaan merkitä $$\left(a^{\frac{1}{n}}\right)^{n}=a^{\frac{1}{n}~\cdot~n}=a^{1}=a.$$
Näin ollen voidaan rinnastaa:
$$a^{\frac{1}{n}}=\sqrt[n]{a}$$
Edelleen voidaan kirjoittaa $$a^{\frac{m}{n}}=a^{\frac{1}{n}~\cdot~m}=\left(a^{\frac{1}{n}}\right)^{m}=\left(\sqrt[n]{a}\right)^{m}.$$
Toisaalta taas $$a^{\frac{m}{n}}=a^{m~\cdot~\frac{1}{n}}=\left(a^{m}\right)^{\frac{1}{n}}=\sqrt[n]{a^{m}}.$$
Siis:
$$a^{\frac{m}{n}}=\left(\sqrt[n]{a}\right)^{m}=\sqrt[n]{a^{m}}$$
Esim. 1
Merkitse juurilausekkeena ja laske arvo.
a) \(9^{\frac{1}{2}}\) b) \(32^{\frac{1}{5}}\) c) \(8^{\frac{2}{3}}\)
Esim. 2
Muuta juurimerkinnäksi.
a) \(a^{-\frac{1}{2}}\) b) \(x^{1{,}5}\)
Esim. 3
Merkitse luvun 3 potenssina.
a) \(\sqrt[5]{3^{4}}\) b) \(\displaystyle{\frac{1}{\sqrt[4]{3}}}\) c) \(3\sqrt{3}\)
Esim. 4
Laske lausekkeen \(\sqrt[10]{a^{5}}\) tarkka arvo.
Esim. 5
Sievennä lauseke \(\displaystyle{\frac{\sqrt{x}}{\sqrt[4]{x}}}\).
Huom.
Potenssi \(a^{x}\) on määritelty kaikilla reaaliluvuilla \(x\), kun \(a>0\). Toisin sanoen eksponentti voi olla myös irrationaaliluku, kuten potenssimerkinnässä \(5^{\sqrt{2}}\).
4.2 Eksponenttifunktio
Funktio on aidosti kasvava tai aidosti vähenevä, jos se saa jokaisen arvonsa täsmälleen kerran.
Täsmällisesti ottaen:
- Funktio \(f\) on aidosti kasvava, jos \(f(x_2)\gt f(x_1)\), kun \(x_2\gt x_1\).
- Funktio \(f\) on aidosti vähenevä, jos \(f(x_2)\lt f(x_1)\), kun \(x_2\gt x_1\).
Funktio \(f\) on aidosti monotoninen, jos se on aidosti kasvava tai aidosti vähenevä.
Eksponenttifunktio
Eksponenttifunktio on muotoa
$$f(x)=a^{x},$$
missä kantaluku \(a\gt 0\) ja \(a\neq1\).
Eksponenttifunktion ominaisuuksia:
- Määrittelyjoukko on \(\mathbb{R}\).
- Arvojoukko on \(\left]0,\infty\right[\) eli \(\mathbb{R_+}\).
- Kuvaaja kulkee pisteen \((0,1)\) kautta.
- Kun \(0\lt a\lt 1\), funktio on aidosti vähenevä.
- Kun \(a\gt 1\), funktio on aidosti kasvava.
Esim. 1
Laske eksponenttifunktion \(f(x)=9^x\) arvo.
a) \(f(2)\) b) \(f\left(\frac{1}{2}\right)\)
Esim. 2
Millä vakion \(t\) arvoilla funktio \(f(x)=(t+2)^x\) on
a) aidosti kasvava b) aidosti vähenevä?
4.3 Logaritmi
Logaritmin määritelmä
$$\log_{a}b=x \quad \Leftrightarrow \quad a^{x}=b,$$
missä \(a\gt 0\), \(a\neq 1\) ja \(b\gt 0\).
Merkintä luetaan "\(a\)-kantainen logaritmi luvusta \(b\) on \(x\)" tai "luvun \(b\) \(a\)-kantainen logaritmi on \(x\)".
Logaritmi on laskutoimitus, joka vastaa kysymykseen, monenteenko potenssiin luku \(a\) on korotettava, jotta saadaan luku \(b\).
Esim. 1
Laske logaritmien arvot.
a) \(\log_{4}16\) b) \(\log_{5}\frac{1}{25}\)
Huom.
\(2\)-, \(e\)- ja \(10\)-kantaisille logaritmeille on vakiintunut käyttöön omat logaritmimerkinnät.
- \(\text{lb}\) (\(2\)-kantainen logaritmi)
- \(\ln\) (\(e\)-kantainen logaritmi)
- \(\lg\) (\(10\)-kantainen logaritmi)
Esim. 2
Laske logaritmien arvot.
a) \(\text{lb}\ 8\) b) \(\lg100\)
Huom.
Lukua \(e\approx2{,}718\) kutsutaan Neperin luvuksi ja \(e\)-kantaista logaritmia luonnolliseksi logaritmiksi.
Logaritmin määritelmästä seuraa:
$$a^{\log_{a}1}=0$$
$$a^{\log_{a}a}=1$$
$$a^{\log_{a}a^{r}}=r$$
$$a^{\log_{a}b}=b$$
Esim. 3
Laske.
a) \(5^{\log_{5}125}\) b) \(e^{\ln7}\)
Esim. 4
Kuinka monta numeroa on luvussa \(4^{2024}\)? Mikä on luvun ensimmäinen numero?
4.4 Logaritmifunktio
Logaritmifunktio
Logaritmifunktio on muotoa
$$f(x)=\log_{a}x,$$
missä kantaluku \(a\gt 0\) ja \(a\neq1\).
Logaritmifunktion ominaisuuksia:
- Määrittelyjoukko on \(\left]0,\infty\right[\) eli \(\mathbb{R_+}\).
- Arvojoukko on \(\mathbb{R}\).
- Kuvaaja kulkee pisteen \((1,0)\) kautta.
- Kun \(0\lt a\lt 1\), funktio on aidosti vähenevä.
- Kun \(a\gt 1\), funktio on aidosti kasvava.
Esim. 5
Mikä on funktion \(f(t)=\log_{3}(t-5)\) määrittelyehto?
4.5 Logaritmin laskusäännöt
Logaritmin laskusääntöjä
- Potenssin logaritmi:$$\log_{a}x^{r}=r\ \log_{a}x$$
- Tulon logaritmi:$$\log_{a}xy=\log_{a}x+\log_{a}y$$
- Osamäärän logaritmi:$$\log_{a}\frac{x}{y}=\log_{a}x-\log_{a}y$$
Kantaluvun vaihto
Olkoon \(a\), \(b\) ja \(x\) positiivisia lukuja ja \(a\), \(b \neq 1\). Tällöin $$\log_{a}x=\displaystyle{\frac{\log_{b}x}{\log_{b}a}}.$$
Perustellaan kantaluvun vaihtoa seuraavalla havainnolla:
Toisaalta logaritmin määritelmän mukaan pätee: $$\begin{align} 4^x&=64\\ x&=\log_{4}64\ (=3). \end{align}$$
Toisaalta taas: $$\begin{align} 4^x&=64\\ \log_{2}4^x&=\log_{2}64 \\ x\cdot\log_{2}4&=\log_{2}64\quad \mid\ :\ \log_{2}4\\ x&=\displaystyle{\frac{\log_{2}64}{\log_{2}4}}\ (=\frac{6}{2}=3). \end{align}$$
Joten on oltava: $$\log_{4}64=\displaystyle{\frac{\log_{2}64}{\log_{2}4}}.$$
4.6 Logaritmiyhtälö
Logaritmiyhtälö
Yhtälöä kutsutaan logaritmiyhtälöksi, jos se voidaan saattaa muotoon $$\log_{a}f(x)=b.$$
Esim. 1
Ratkaise yhtälö \(\log_{4}(3x+1)=2\).
Esim. 2
Ratkaise yhtälö \(\log_{7}(x+2)+\log_{7}(x+4)=3\log_{7}2\).
Esim. 3
Ratkaise yhtälö \(\lg(x^{2}-2x)-\lg3x=2\lg5\).
4.7 Eksponenttiyhtälö
Eksponenttiyhtälö
Yhtälöä kutsutaan eksponenttiyhtälöksi, jos se voidaan saattaa muotoon $$a^{f(x)}=b,$$ missä \(a>0\) ja \(a\neq1\) sekä \(b>0\).
Esim. 1
Ratkaise yhtälö.
a) \(7^{x}=30\) b) \(2^{x}=-8\)
Esim. 2
Ratkaise yhtälö.
a) \(2^{3x+5}=4\) b) \(9^{x}=\frac{1}{\sqrt{3}}\)
Esim. 3
Ratkaise yhtälö.
\(5\cdot4^{2x-1}-325=175\)
4.8 Eksponentiaalinen muutos
Eksponentiaalista muutosta ajan kuluessa voidaan mallintaa funktiolla $$f(x)=ka^x,$$ missä
- \(k\ (\gt0)\) on tietyn suureen arvo alkuhetkellä,
- \(a\) ilmoittaa kuinka moninkertaiseksi suure muuttuu peräkkäisissä yhtä pitkissä aikaväleissä ja
- \(x\) on peräkkäisten aikavälien lukumäärä.
Funktio \(f\) kuvaa
- eksponentiaalista vähenemistä, jos \(0\lt a\lt1\),
- eksponentiaalista kasvua, jos \(a\gt1\).
Esim. 1
Bakteerien määrä kasvaa 50 % puolessa tunnissa. Alkuhetkellä bakteereja on 200.
a) Kuinka paljon bakteereja on neljän tunnin kuluttua?
b) Kuinka paljon bakteereja oli 75 minuuttia ennen alkuhetkeä?
c) Kuinka pitkän ajan kuluttua bakteereja on 10 000?
4.9 Kuvaajan sovittaminen
Kuvaajan sovittaminen tunnettuun pistejoukkoon voidaan suorittaa GeoGebran taulukkolaskennalla käyttäen Kahden muuttujan regressioanalyysiä. Alasvetovalikosta valitaan parhaiten pistejoukkoon sopiva regressiomalli. GeoGebra ilmoittaa mallin mukaisen funktion lausekkeen ja laskee annettua muuttujan arvoa vastaavan funktion arvon tai toisinpäin.