Derivaatta (MAA6)
Laajuus
3 op
Yleiset tavoitteet (LOPS 2021)
Moduulin tavoitteena on, että opiskelija
- tutustuu ilmiöiden matemaattisten mallien käyttäytymiseen derivaatan avulla
- omaksuu havainnollisen käsityksen funktion raja-arvosta ja jatkuvuudesta
- ymmärtää derivaatan tulkinnan funktion muutosnopeutena
- kykenee määrittämään yksinkertaisten funktioiden derivaatat
- osaa derivoida yhdistettyjä funktioita
- hallitsee funktioiden kulun tutkimisen derivaatan avulla ja osaa määrittää niiden ääriarvot suljetulla välillä
- osaa käyttää ohjelmistoja raja-arvon, jatkuvuuden ja derivaatan tutkimisessa sovellusten yhteydessä.
Keskeiset sisällöt (LOPS 2021)
- funktion raja-arvo, jatkuvuus ja derivaatta
- polynomi- ja rationaalifunktioiden sekä juurifunktion derivaatat
- sini- ja kosinifunktioiden sekä eksponentti- ja logaritmifunktioiden derivaatat
- funktioiden tulon ja osamäärän derivaatta
- yhdistetty funktio ja sen derivointi
- funktion kulun tutkiminen ja ääriarvojen määrittäminen
Aikataulu
Suoritus
- osallistuminen
- tehtävien tekeminen
- monivalintatehtävien tekeminen
- pistokoe
- 3 osakoetta
Arviointi
- säännöllinen, aktiivinen ja vastuullinen osallistuminen +1 p
- tehtävien asianmukainen ja jatkuva tekeminen +1 p
- monivalintatehtävistä +1 p kustakin tehdystä monivalintakokonaisuudesta, saavutettava tavoitetaso 80 %, yht. max. 8 p
- pistokokeesta max. 5 p
- osakokeista max. 36 p kustakin
- max. 120 p (teoreettisesti 123 p)
- 30 % arviointi
| Pisteet | Arvosana | Muuta |
|---|---|---|
| 0 - 17 | i \(\rightarrow\) K | Pakko täydentää. |
| 18 - 35 | 4 | Oikeus täydentää. |
| 36 - 51 | 5 | |
| 52 - 67 | 6 | |
| 68 - 83 | 7 | |
| 84 - 99 | 8 | |
| 100 - 117 | 9 | |
| 118 - 120 | 10 |
Keskeyttäminen
Opettaja keskeyttää opiskelijan opintojakson, jos
- opiskelija niin pyytää
- opiskelija ei ole läsnä opintojakson kahdella ensimmäisellä opetuskerralla ja opiskelija ei ole yhteydessä opettajaan eikä opettaja saa yhteyttä opiskelijaan.
Opettaja voi keskeyttää opiskelijan opintojakson, jos opiskelijalla on neljä poissaoloa. Tällaiset tilanteet opettaja käy läpi tapauskohtaisesti ja on ennen lopullista keskeytystä yhteydessä opiskelijaan.
Keskeyttämisestä opettaja merkitsee opintojaksosta opiskelijalle K-merkinnän Wilmaan ja poistaa opiskelijan sen jälkeen Wilman ryhmästä. Opettaja lähettää keskeyttämisestä viestin opiskelijalle, alaikäisen opiskelijan huoltajalle, ryhmänohjaajalle ja opolle.
1 RAJA-ARVO JA JATKUVUUS
1.1 Raja-arvo
Esim. 1
Rationaalifunktio \(\displaystyle{f(x)=\frac{x^{2}-1}{x-1}}\) ei ole määritelty nimittäjän nollakohdassa \(x=1\). Tutkitaan funktion \(f\) arvoja kohdan \(x=1\) läheisyydessä.
\(\begin{array}{|l|l|} \hline \mathbf{Lähestyy\ vasemmalta} & \mathbf{Lähestyy\ oikealta}\\ \hline f(0{,}9)=1{,}9 & f(1{,}1)=2{,}1\\ f(0{,}99)=1{,}99 & f(1{,}01)=2{,}01\\ f(0{,}999)=1{,}999 & f(1{,}001)=2{,}001\\ f(0{,}9999)=1{,}9999 & f(1{,}0001)=2{,}0001\\ f(0{,}99999)=1{,}99999 & f(1{,}00001)=2{,}00001\\ \hline \end{array} \)
Raja-arvon määritelmä
Funktiolla \(f\) on kohdassa \(x=a\)
- vasemmanpuolinen raja-arvo \(b\), jos funktion arvo lähestyy lukua \(b\), kun muuttujan \(x\) arvo lähestyy lukua \(a\) vasemmalta puolelta eli $$\lim_{x\to a-} f(x)=b$$
- oikeanpuolinen raja-arvo \(b\), jos funktion arvo lähestyy lukua \(b\), kun muuttujan \(x\) arvo lähestyy lukua \(a\) oikealta puolelta eli $$\lim_{x\to a+} f(x)=b$$
- raja-arvo \(b\), jos funktion arvo lähestyy lukua \(b\), kun muuttujan \(x\) arvo lähestyy luku \(a\) kummalta puolelta tahansa eli funktion toispuoliset raja-arvot ovat yhtä suuret: $$\lim_{x\to a} f(x)=b \quad \Leftrightarrow \quad \lim_{x\to a-} f(x)=\lim_{x\to a+} f(x)=b.$$
Esim. 2
Kuvassa on funktion \(\displaystyle{f(x)=\frac{x^{2}-1}{x-1}}\) kuvaaja.
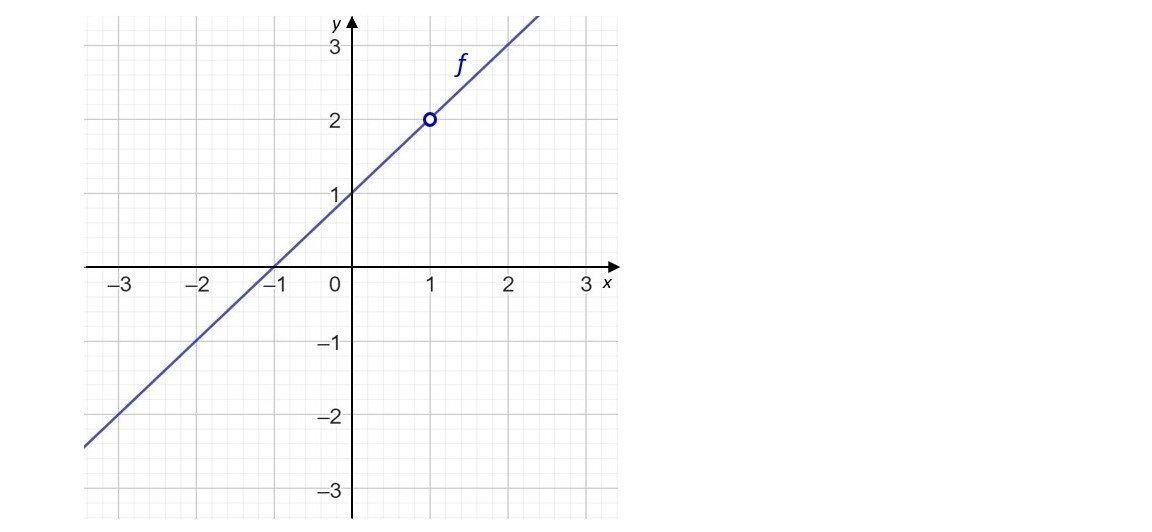
a) Onko funktiolla \(f\) arvo kohdassa \(x=1\)?
b) Onko funktiolla \(f\) vasemmanpuolinen raja-arvo kohdassa \(x=1\)?
c) Onko funktiolla \(f\) oikeanpuolinen raja-arvo kohdassa \(x=1\)?
d) Onko funktiolla \(f\) raja-arvo kohdassa \(x=1\)?
Esim. 3
Funktio \(f\) on määritelty paloittain \(f(x)=\begin{cases}x+1, & \text{kun}\ x\ge2\\x^{2}-2, & \text{kun}\ x\lt2\end{cases}\).
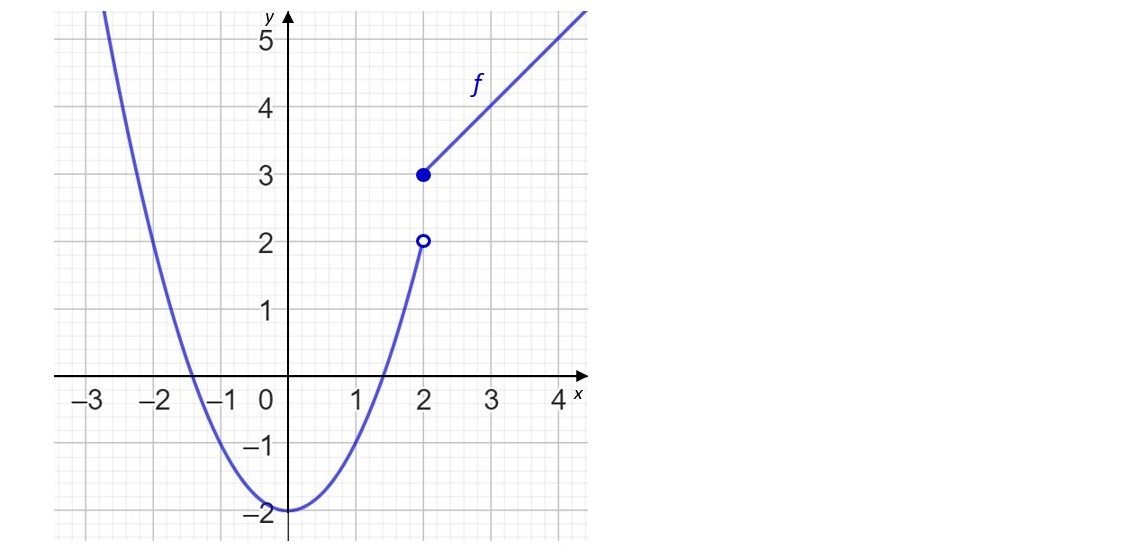
a) Onko funktiolla \(f\) arvo kohdassa \(x=2\)?
b) Onko funktiolla \(f\) vasemmanpuolinen raja-arvo kohdassa \(x=2\)?
c) Onko funktiolla \(f\) oikeanpuolinen raja-arvo kohdassa \(x=2\)?
d) Onko funktiolla \(f\) raja-arvo kohdassa \(x=2\)?
Huom.
GeoGebralla paloittain määritellyn funktion kuvaaja voidaan piirtää vaikkapa käyttäen komentoa Jos(ehto,niin,muutoin).
1.2 Raja-arvon laskeminen
Raja-arvon laskusääntöjä
Olkoon funktioilla \(f\) ja \(g\) raja-arvo kohdassa \(a\). Olkoon lisäksi \(k\) reaaliluku.
- Vakion raja-arvo $$\lim_{x\to a}k=k$$
- Identtisen funktion raja-arvo $$\lim_{x\to a}x=a$$
- Vakion siirtosääntö $$\lim_{x\to a}\left(k\cdot f(x)\right)=k\cdot\left(\lim_{x\to a}f(x)\right)$$
- Funktioiden summan raja-arvo $$\lim_{x\to a}\left(f(x)+g(x)\right)=\lim_{x\to a}f(x)+\lim_{x\to a}g(x)$$
- Funktioiden tulon raja-arvo $$\lim_{x\to a}\left(f(x)g(x)\right)=\lim_{x\to a}f(x)\cdot\lim_{x\to a}g(x)$$
Esim. 1
Laske raja-arvo \(\displaystyle{\lim_{x\to2}(3x^{2}-4x+1})\).
Osamäärän raja-arvo
- Jos \(\displaystyle{\lim_{x\to a}g(x)\neq0}\), niin \(\displaystyle{\lim_{x\to a}\frac{f(x)}{g(x)}}=\frac{\displaystyle{\lim_{x\to a}f(x)}}{\displaystyle{\lim_{x\to a}g(x)}}\).
- Jos \(\displaystyle{\lim_{x\to a}g(x)=0}\) ja \(\displaystyle{\lim_{x\to a}f(x)\neq0}\), niin äärellistä raja-arvoa \(\displaystyle{\lim_{x\to a}\frac{f(x)}{g(x)}}\) ei ole olemassa.
- Jos \(\displaystyle{\lim_{x\to a}g(x)=0}\) ja \(\displaystyle{\lim_{x\to a}f(x)=0}\), niin lausekkeelle \(\displaystyle{\frac{f(x)}{g(x)}}\) voidaan mahdollisesti määrittää raja-arvo sieventämällä lauseketta.
Esim. 2
Laske raja-arvo.
a) \(\displaystyle{\lim_{x\to -1}\frac{2x+5}{3x^{2}+3}}\)
b) \(\displaystyle{\lim_{x\to 1}\frac{2x+5}{3x^{2}-3}}\)
c) \(\displaystyle{\lim_{x\to -2}\frac{2x^{2}+4x}{3x+6}}\)
Esim. 3
Laske raja-arvo.
a) \(\displaystyle{\lim_{x\to 1}\frac{x^{2}-1}{x-1}}\)
b) \(\displaystyle{\lim_{x\to 3}\frac{2x-6}{x^{2}-9}}\)
Huom.
GeoGebralla raja-arvoja voi määrittää seuraavilla komennoilla.
RajaArvo(Funktio,Arvo)RajaArvoOikea(Funktio,Arvo)RajaArvoVasen(Funktio,Arvo)
1.3 Funktion jatkuvuus
Määritelmä
Funktio \(f\) on jatkuva kohdassa \(x=a\), jos funktion \(f\) raja-arvo on sama kuin funktion \(f\) arvo kohdassa \(x=a\) eli $$\lim_{x\to a}f(x)=f(a).$$
Siis funktion \(f\) jatkuvuus kohdassa \(x=a\) edellyttää, että
- funktio \(f\) on määritelty kohdassa \(x=a\),
- funktiolla \(f\) on raja-arvo kohdassa \(x=a\) ja
- funktion \(f\) raja-arvo ja funktion \(f\) arvo kohdassa \(x=a\) ovat yhtä suuret.
Huom.
Jos funktiota ei ole määritelty jossakin kohdassa, ei tässä kohdassa ole mielekästä puhua jatkuvuudesta laisinkaan.
Jos funktio on määritelty, mutta ei jatkuva jossakin kohdassa, voimme sanoa, että funktio on epäjatkuva tässä kohdassa.
Esim. 1.
Onko funktio \(f\) jatkuva kohdassa \(x=1\)?
(Tehtävään liittyvä kuva esillä oppitunnilla.)
Esim. 2.
Miten funktio \(f(x)=\frac{2x^{2}-4x}{x-2}\) tulisi määritellä, jotta se olisi jatkuva kohdassa \(x=2\)?
Funktion jatkuvuus välillä
Toispuolisesti jatkuva funktio
Funktio \(f\) on kohdassa \(x=a\)
- vasemmalta jatkuva, jos funktion \(f\) vasemmanpuolinen raja-arvo on yhtä suuri kuin funktion arvo kohdassa \(x=a\), $$\lim_{x\to a-}f(x)=f(a)$$
- oikealta jatkuva, jos funktion \(f\) oikeanpuolinen raja-arvo on yhtä suuri kuin funktion arvo kohdassa \(x=a\), $$\lim_{x\to a+}f(x)=f(a)$$
- toispuolisesti jatkuva, jos se on vasemmanpuolisesti jatkuva tai oikeanpuolisesti jatkuva.
| Merkintä | Vastaavuus | Määre |
|---|---|---|
| \(\left[a,b\right]\) | \(a\le x \le b\) | suljettu väli |
| \(\left[a,b\right[\) | \(a\le x \lt b\) | puoliavoin väli |
| \(\left]a,b\right]\) | \(a\lt x \le b\) | puoliavoin väli |
| \(\left]a,b\right[\) | \(a\lt x \lt b\) | avoin väli |
Funktion jatkuvuus välillä
Funktio \(f\) on jatkuva välillä \(I\), jos funktio \(f\) on jatkuva välin \(I\) jokaisessa sisäpisteessä ja toispuolisesti jatkuva väliin \(I\) kuuluvissa päätepisteissä.
Huom.*
Määritelmästä seuraa, että funktio \(f\) on jatkuva suljetulla välillä \(\left[a,b\right]\) vain, jos
- funktio \(f\) on määritelty välin \(\left[a,b\right]\) jokaisessa pisteessä,
- funktiolla \(f\) on raja-arvo \(f(x_0)\) kaikilla muuttujan arvoilla \(x_0\), jotka kuuluvat avoimelle välille \(\left]a,b\right[\),
- funktiolla \(f\) on toispuoliset raja-arvot \(\lim_{x\to a+}f(x)=f(a)\) ja \(\lim_{x\to b-}f(x)=f(a)\).
Esim. 3
Onko funktio jatkuva välillä? (Kuva esillä oppitunnilla.)
Sanomme lisäksi, että funktio \(f\) on
- kaikkialla jatkuva, jos se on jatkuva koko reaalilukujoukossa,
- jatkuva, jos se on jatkuva koko määrittelyjoukossaan.
Huom.
Alkeisfunktiot ja niistä peruslaskutoimituksilla, itseisarvolla ja yhdistämällä muodostetut funktiot ovat määrittelyjoukossaan jatkuvia.
2 DERIVAATTA
2.1 Derivaatan geometrinen merkitys
Esim. 1
Kappaleen sijaintia eri ajanhetkinä sen pudotessa Maan painovoimakentässä voidaan karkeasti kuvata funktiolla \(f(x)=5x^2\), missä \(x\) on aika putoamisen alkamisesta sekunteina. Määritä kappaleen
a) keskinopeus aikavälillä 2 s ... 4 s
b) hetkellinen nopeus ajanhetkellä 2 s.
Derivaatan geometrinen merkitys
Funktion \(f\) derivaatta \(f'(a)\) on funktion kuvaajalle kohtaan \(x=a\) piirretyn tangentin kulmakerroin.
Funktion \(f\) kuvaaja ja sille kohtaan \(x=a\) piirretty tangentti ovat kohdassa \(x=a\) yhdensuuntaiset. Funktion \(f\) derivaatta \(f'(a)\) ilmaisee funktion \(f\) arvojen hetkellisen muutosnopeuden kohdassa \(a\).
Funktio \(f\) on derivoituva kohdassa \(x=a\), jos funktion kuvaajalle kohtaan \(x=a\) voidaan piirtää tangentti, joka ei ole pystysuora.
2.2 Derivaatan määritelmä
Määritetään funktion \(f\) derivaatan \(f'(a)\) arvo kohdassa \(a\) laskennallisesti kahdella vaihtoehtoisella tavalla.
Tapa 1
Määritetään funktion \(f\) kuvaajan pisteiden \(\left(a,f(a)\right)\) ja \(\left(a+h,f(a+h)\right)\) kautta kulkevan sekantin kulmakertoimen lauseke. $$\frac{f(a+h)-f(a)}{(a+h)-a}=\frac{f(a+h)-f(a)}{h}$$ Lauseketta kutsutaan erotusosamääräksi.
Kun pistettä \(\left(a+h,f(a+h)\right)\) siirretään kohti pistettä \(\left(a,f(a)\right)\), eli pisteiden välistä etäisyyttä \(h\) pienennetään, sekantin kulmakertoimen arvo lähestyy pisteeseen \(\left(a,f(a)\right)\) piirretyn tangentin kulmakertoimen arvoa. Kulmakertoimen arvo eli derivaatta kohdassa \(a\) on siis erotusosamäärän raja-arvo kohdassa \(a\), kun \(h\) lähestyy nollaa. $$\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}$$
Tapa 2
Funktion \(f\) kuvaajan ja sekantin laikkauspisteitä voidaan merkitä myös \(\left(a,f(a)\right)\) ja \(\left(x,f(x)\right)\). Tällöin sekantin kulmakertoimen lauseke voidaan esittää muodossa $$\frac{f(x)-f(a)}{x-a}$$ Tätäkin lauseketta kutsutaan erotusosamääräksi.
Erotusosamäärän raja-arvo kohdassa \(a\) saa nyt seuraavan muodon. $$\lim_{x\to a}\frac{f(x)-f(a)}{x-a}$$
Derivaatta
Funktion \(f\) derivaatta kohdassa \(a\) on $$f'(a)=\lim_{x\to h}\frac{f(a+h)-f(a)}{h}=\lim_{x\to a}\frac{f(x)-f(a)}{x-a},$$ jos tällainen raja-arvo on olemassa.
Esim. 1
Määritä funktion \(f(x)=x^{2}+3x\) derivaatta kohdassa \(x=-1\).
\(\begin{align} f'(a)&=\lim_{h\to0}\frac{f(a+h)-f(a)}{h}\quad\quad\ \ \mid\,a=-1\\ \\ f'(-1)&=\lim_{h\to0}\frac{f(-1+h)-f(-1)}{h}\quad\mid\,f(x)=x^{2}+3x\\ \\ &=\lim_{h\to0}\frac{(-1+h)^{2}+3(-1+h)-((-1)^{2}+3\cdot(-1))}{h}\\ \\ &=\lim_{h\to0}\frac{(-1)^{2}+2\cdot(-1)h+h^{2}-3+3h-(1-3)}{h}\\ \\ &=\lim_{h\to0}\frac{1-2h+h^{2}-3+3h-(-2)}{h}\\ \\ &=\lim_{h\to0}\frac{h+h^{2}\cancel{-2}\cancel{+2}}{h}\\ \\ &=\lim_{h\to0}\frac{\cancel{h}(1+h)}{\cancel{h}}\\ \\ &=1+0\\ \\ &=1 \end{align}\)
Vastaus: \(f'(-1)=1\).
Huom.
Sanomme, että funktio \(f\) on
- derivoituva kohdassa \(a\), jos funktiolla on derivaatta kohdassa \(a\),
- kaikkialla derivoituva, jos se on derivoituva koko reaalilukujoukossa,
- derivoituva, jos se on derivoituva koko määrittelyjoukossaan.
Derivaattafunktio
Monesti haluamme selvittää lausekkeen, jolla saisimme laskettua funktion derivaatan arvon mille tahansa muuttujan arvolle \(x\).
Derivaattafunktio
Funktion \(f\) derivaattafunktio \(f'\) on funktio, jonka arvo \(f'(x)\) on funktion \(f\) derivaatta muuttujan arvolla \(x\). $$f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$$
Toimenpidettä, jolla määritetään funktion derivaattafunktio, kutsutaan derivoinniksi.
Esim. 2
Määritä funktion \(f(x)=2x^{3}\) derivaattafunktio. Laske derivaattafunktion avulla derivaatat \(f'(0)\) ja \(f'(1)\).
\(\begin{align} f'(x)&=\lim_{h\to0}\frac{f(x+h)-f(x)}{h}\quad\mid\,f(x)=2x^{3}\\ \\ &=\lim_{h\to0}\frac{2(x+h)^{3}-2x^{3}}{h}\\ \\ &=\lim_{h\to0}\frac{2(x+h)^{2}(x+h)-2x^{3}}{h}\\ \\ &=\lim_{h\to0}\frac{2(x^{2}+2xh+h^{2})(x+h)-2x^{3}}{h}\\ \\ &=\lim_{h\to0}\frac{2(x^{3}+x^{2}h+2x^{2}h+2xh^{2}+xh^{2}+h^{3})-2x^{3}}{h}\\ \\ &=\lim_{h\to0}\frac{\cancel{2x^{3}}+2x^{2}h+4x^{2}h+4xh^{2}+2xh^{2}+2h^{3}\cancel{-2x^{3}}}{h}\\ \\ &=\lim_{h\to0}\frac{\cancel{h}(2x^{2}+4x^{2}+4xh+2xh+2h^{2})}{\cancel{h}}\\ \\ &=2x^{2}+4x^{2}+4x\cdot0+2x\cdot0+2\cdot0^{2}\\ \\ &=6x^{2} \end{align}\)
\(f'(0)=6\cdot0^{2}=0\)
\(f'(1)=6\cdot1^{2}=6\)
Vastaus: \(f'(x)=6x^{2},\ f'(0)=0,\ f'(1)=6\).
3 POLYNOMIFUNKTIO
3.1 Polynomifunktion derivointi
Derivointi derivaattafunktion määritelmään nojautuen on työlästä. Määritelmästä onkin johdettu erilaisille funktioille omia derivoimiskaavojaan sujuvoittamaan käytännön laskemista.
Merkintä
Funktion \(f(x)\) derivaattafunktio voidaan merkitä \(f'(x)\) tai \(\text{D}~f(x)\) tai \(\frac{\text{d}}{\text{d}x}f(x)\).
Potenssifunktion derivoimiskaava
\(\text{D}\,x^n=nx^{n-1}\)
Seuraavat derivoimissäännöt voidaan johtaa raja-arvon laskusäännöistä.
Derivoimissääntöjä
Olkoot \(k\) reaaliluku ja \(f\) ja \(g\) derivoituvia funktioita.
- \(\text{D}\,k=0\)
- \(\text{D}\,kx=k\)
- \(\text{D}\,kf(x)=k~\text{D}f(x)=kf'(x)\)
- \(\text{D}\left(f(x)+g(x)\right)=\text{D}~f(x)+\text{D}\,g(x)=f'(x)+g'(x)\)
Esim. 1
Derivoi.
a) \(x^5\) b) \(-4x^3\) c) \(\frac{2x^6}{3}\)
a) \(\text{D}\,x^5=5x^4\) b) \(\text{D}\left(-4x^3\right)=-4\cdot 3x^2=-12x^2\) c) \(\text{D}\,\frac{2x^6}{3}=\frac{2}{3}\cdot6x^5=4x^5\)
Esim. 2
Derivoi polynomifunktiot.
a) \(f(x)=3x^2+4x+5\) b) \(g(x)=2x^{5}-\frac{3}{2}x^{4}+x^{3}+\frac{1}{2}x^{2}\)
a) \(f'(x)=3\cdot2x+4=6x+4\)
b) \(g'(x)=2\cdot5x^4-\frac{3}{2}\cdot4x^3+3x^2+\frac{1}{2}\cdot2x=10x^4-6x^3+3x^2+x\)
Esim. 3
Laske funktion derivaatan arvo kohdassa \(-1\).
a) \(f(x)=2x^4+5x+12\) b) \(s(t)=2t(t+3)^2\)
a) Derivoidaan.
\(\begin{align}f'(x)&=2\cdot4x^3+5\\&=8x^3+5\end{align}\)
Lasketaan derivaatta (eli derivaattafunktion arvo) kohdassa \(-1\).
\(\begin{align}f'(-1)&=8\cdot(-1)^3+5\\&=8\cdot(-1)+5\\&=-8+5\\&=-3\end{align}\)
Vastaus: \(f'(-1)=-3\)
b) Sievennetään funktion lauseke polynomiksi.
\(\begin{align}s(t)&=2t(t+3)^2\quad\quad\quad\mid(a+b)^2=a^2+2ab+b^2\\&=2t(t^2+6t+9)\\&=2t^3+12t^2+18t\end{align}\)
Derivoidaan.
\(\begin{align}s'(t)&=2\cdot3t^2+12\cdot2t+18\\&=6t^2+24t+18\end{align}\)
Lasketaan derivaatta kohdassa \(-1\).
\(\begin{align}s'(-1)&=6\cdot(-1)^2+24\cdot(-1)+18\\&=6\cdot1-24+18\\&=6-24+18\\&=0\end{align}\)
Vastaus: \(s'(-1)=0\)
Huom.
Funktion derivaattafunktio saadaan määritettyä GeoGebralla komennolla Derivaatta(funktio,muuttuja).
3.2 Tangentin yhtälö
Suoran yhtälö voidaan määrittää, jos tunnetaan suoran kulmakerroin ja yksi suoran piste.
Suoran yhtälö
Olkoon \(k\) suoran kulmakerroin ja \((x_0,y_0)\) yksi suoran piste. Tällöin suoran yhtälö on $$y-y_0=k(x-x_0).$$
Tämän perusteella saadaan funktion \(f\) kuvaajalle kohtaan \(x_0\) piirretyn tangentin yhtälö.
Funktion kuvaajan tangentin yhtälö
Olkoon \(f'(x_0)\) funktion \(f(x)\) derivaatta kohdassa \(x_0\). Tällöin funktion kuvaajalle kohtaan \(x_0\) piirretyn tangentin yhtälö on $$y-f(x_0)=f'(x_0)(x-x_0).$$
Kohtisuoruusehdon mukaan: $$k_1\cdot k_2=-1\quad \Longleftrightarrow\quad k_2=-\frac{1}{k_1}.$$
Näin ollen.
Funktion kuvaajan normaalin yhtälö
Olkoon \(f'(x_0)\) funktion \(f(x)\) derivaatta kohdassa \(x_0\). Tällöin funktion kuvaajalle kohtaan \(x_0\) piirretyn normaalin yhtälö on $$y-f(x_0)=-\frac{1}{f'(x_0)}(x-x_0),$$ kun \(f'(x_0)\neq0\), ja $$x=x_0,$$ kun \(f'(x_0)=0\).
Esim. 1
Määritä funktion \(f(x)=3x^2-x\) kuvaajalle kohtaan \(x=1\) piirrettyjen tangentin ja normaalin yhtälöt.
\(f(1)=3\cdot1^2-1=3\cdot1-1=3-1=2\)
\(f'(x)=6x-1\)
\(f'(1)=6\cdot1-1=6-1=5\)
Tangentin yhtälö:
\(\begin{align} y-f(x_0)&=f'(x_0)(x-x_0)\\ y-f(1)&=f'(1)(x-1)\\ y-2&=5(x-1)\\ y-2&=5x-5\quad\mid\ +2\\ y&=5x-3 \end{align}\)
Normaalin yhtälö:
\(\begin{align} y-f(x_0)&=-\frac{1}{f'(x_0)}(x-x_0)\\ y-f(1)&=-\frac{1}{f'(1)}(x-1)\\ y-2&=-\frac{1}{5}(x-1)\\ y-2&=-\frac{1}{5}x+\frac{1}{5}\quad\mid\ +2\\ y&=-\frac{1}{5}x+\frac{11}{5} \end{align}\)
Vastaus: Tangentin yhtälö on \(y=5x-3\) ja normaalin \(y=-\frac{1}{5}x+\frac{11}{5}\)
3.3 Kuvaajan kulku
Funktion monotonisuus
Olkoot \(a\), \(b\), \(x_1\) ja \(x_2\) reaalilukuja, ja \(x_1\) ja \(x_2\) kuuluvat välille \(\left[a,b\right]\). Olkoon lisäksi \(f\) välillä \(\left[a,b\right]\) jatkuva funktio.
Tällöin funktio \(f\) on välillä \(\left[a,b\right]\)
- aidosti kasvava, jos \(x_1\lt x_2\) ja \(f(x_1)\lt f(x_2)\)
- aidosti vähenevä, jos \(x_1\lt x_2\) ja \(f(x_1)\gt f(x_2)\)
- aidosti monotoninen, jos se on aidosti kasvava tai aidosti vähenevä.
Esim. 1
Tutkitaan funktion \(f(x)=x^7+x^5-4x^3+1\) kuvaajalle eri kohtiin piirretyn tangentin kulmakertoimen arvoja.
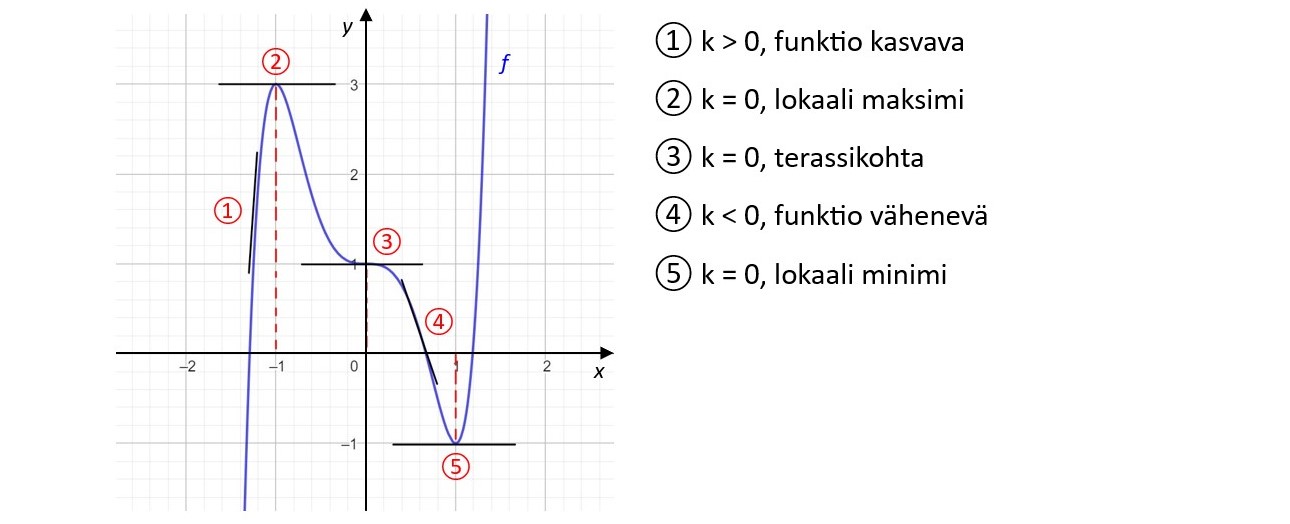
Funktion monotonisuus ja derivaatta
Olkoon \(f\) välillä \(I\) derivoituva funktio.
- Jos \(f'(x)\gt0\) välillä \(I\) lukuun ottamatta yksittäisiä kohtia, joissa \(f′(x) = 0\), niin funktion kuvaaja on nouseva ja funktio on aidosti kasvava tuolla välillä.
- Jos \(f'(x)\lt0\) välillä \(I\) lukuun ottamatta yksittäisiä kohtia, joissa \(f′(x) = 0\), niin funktion kuvaaja on laskeva ja funktio aidosti vähenevä tuolla välillä.
Derivaattafunktion nollakohdat
Derivaattafunktion nollakohta tarkoittaa muuttujan \(x\) arvoa, jolla derivaattafunktio saa arvon nolla.
Huom.
Derivaattafunktion nollakohdat ovat samalla funktion ääriarvokohtia tai terassikohtia.
Funktion ääriarvokohdat
- Minikohta on muuttujan \(x\) arvo, jolla funktio saa paikallisesti pienimmän arvonsa eli minimiarvonsa.
- Maksimikohta on muuttujan \(x\) arvo, jolla funktio saa paikallisesti suurimman arvonsa eli maksimiarvonsa.
Huom.
Ääriarvokohdassa funktion kuvaajan kulkusuunta vaihtuu.
Esim. 2
Tutki funktion \(f(x)=x^7+x^5-4x^3+1\) kulkua laskemalla.
a) Määritä derivaattafunktion nollakohdat.
b) Laadi kulkukaavio.
c) Päättele funktion monotonisuus eri väleillä.
d) Päättele funktion ääriarvokohdat ja niiden laatu.
a) Derivoidaan.
\(\begin{align} f'(x)&=7x^{6}+5x^{4}-4\cdot3x^{2}\\ \\ &=7x^{6}+5x^{4}-12x^{2} \end{align}\)
Derivaattafunktion nollakohdat:
\( \begin{align} f'(x)&=0\\ \\ 7x^{6}+5x^{4}-12x^{2}&=0\quad\mid\text{CAS-laskin}\\ \\ x=-1,\quad x&=0\quad\text{tai}\quad x=1 \end{align} \)
(Oppitunnilla näytetään yhtälön ratkaiseminen käsin.)
b) Kulkukaavio:
\( \begin{array}{lccccccc} &&-1&&0&&1&\\ \hline f'(x)&+&\mid&-&\mid&-&\mid&+\\ \hline f(x)&\nearrow&\mid&\searrow&\mid&\searrow&\mid&\nearrow\\ \end{array} \)
Testipisteet:
\(f'(-2)=7\cdot(-2)^{6}+5\cdot(-2)^{4}-12\cdot(-2)^{2}=480\gt0\)
\(f'(-\frac{1}{2})=7\cdot(-\frac{1}{2})^{6}+5\cdot(-\frac{1}{2})^{4}-12\cdot(-\frac{1}{2})^{2}=-\frac{165}{64}\lt0\)
\(f'(\frac{1}{2})=7\cdot(\frac{1}{2})^{6}+5\cdot(\frac{1}{2})^{4}-12\cdot(\frac{1}{2})^{2}=-\frac{165}{64}\lt0\)
\(f'(2)=7\cdot2^{6}+5\cdot2^{4}-12\cdot2^{2}=480\gt0\)
c) Kulkukaavion perusteella väleillä \(x\lt-1\) ja \(x\gt1\) funktio on aidosti kasvava ja välillä \(-1\lt x\lt1\) aidosti vähenevä.
d)Kulkukaavion perusteella funktion \(f\) ääriarvokohdat ovat \(x=-1\) ja \(x=1\). Kohta \(x=-1\) on maksimikohta ja \(x=1\) minimikohta.
(Huom. Kohta \(x=0\) on terassikohta, ei ääriarvokohta.)
3.4 Suurin ja pienin arvo
Esim. 1
Määritä laskemalla funktion \(f(x)=\frac{1}{4}x^4+\frac{1}{3}x^3-x^2\) suurin ja pienin arvo.
Lause
Olkoon \(f\) suljetulla välillä \(\left[a,b\right]\) jatkuva funktio.
1) Funktiolla \(f\) on aina suurin ja pienin arvo.
2) Jos funktio \(f\) on lisäksi derivoituva avoimella välillä \(\left]a,b\right[\), niin se saavuttaa suurimman ja pienimmän arvonsa välille \(\left]a,b\right[\) kuuluvassa derivaattafunktion nollakohdassa tai välin \(\left[a,b\right]\) päätepisteessä.
Lause
Suljetulla välillä jatkuva funktio saa tällä välillä pienimmän ja suurimman arvonsa sekä kaikki arvot niiden väliltä.
Esim. 2
Määritä funktion \(f(x)=\frac{1}{4}x^4+\frac{1}{3}x^3-x^2\) suurin ja pienin arvo välillä \(\left[-1,1\right]\).
3.5 Bolzanon lause
Bolzanon lause
Jos funktio \(f\) on jatkuva suljetulla välillä \(\left[a,b\right]\) ja funktion \(f\) arvot ovat erimerkkiset tämän välin päätepisteissä, niin funktiolla on vähintään yksi nollakohta avoimella välillä \(\left]a,b\right[\).
Jos lisäksi funktio \(f\) on aidosti monotoninen avoimella välillä \(\left]a,b\right[\), niin voidaan varmasti sanoa, että nollakohtia on täsmälleen yksi.
Esim. 1
Käydään oppitunnilla oppikirjan kappaleen 10 esimerkki 1.
3.6 Ääriarvotehtävä 1
Esim. 1
Suorakulmion muotoisen aitauksen ympärysmitta on 30 metriä. Mitä on aitauksen mittojen (pituus ja leveys) oltava, että aitauksen pinta-ala olisi suurin mahdollinen?
Merkitään aitauksen pituutta \(a\) ja leveyttä \(h\). Tällöin pinta-ala on \(A=ah\).
Pinta-alan suurin arvo voidaan löytää derivoimalla pinta-alan lauseketta suljetulla välillä. Pinta-alan suurin arvo löytyy derivaattafunktion nollakohdista tai välin päätepisteistä.
Valitaan derivoitavaksi muuttujaksi pituus \(a\). Ratkaistaan suorakulmion piirin lausekkeesta \(h\) pituuden \(a\) suhteen.
\(\begin{align} 2a+2h&=30\\ h&=\displaystyle{\frac{30-2a}{2}=15-a} \end{align}\)
Määritellään aitauksen pinta-ala funktiona.
\(\begin{align} A(x)&=ah\quad\quad\quad\qquad \mid h=15-a\\ &=a(15-a)\\ &=15a-a^2 \end{align}\)
Aitauksen mittojen on oltava epänegatiivisia.
\(\begin{align} a\ge0\quad\quad\quad\text{ja}\quad\quad\quad h&\ge0\quad \mid h=15-a\\ 15-a&\ge0\\ 15&\ge a \end{align}\)
Määritetään siis funktion \(A\) suurin arvo välillä \(\left[0,15\right]\).
Derivoidaan.
\(A'(x)=15-2a\)
Derivaattafunktion nollakohdat:
\(\begin{align} A'(x)&=0\\ 15-2a&=0\\ a&=\frac{15}{2} \end{align}\)
Lasketaan funktion \(A\) arvot derivaattafunktion nollakohdassa ja välin \(\left[0,15\right]\) päätepisteissä.
\(A(0)=15\cdot0-0^2=0\)
\(A\left(\frac{15}{2}\right)=15\cdot\frac{15}{2}-\left(\frac{15}{2}\right)^2=\frac{225}{4}\)
\(A(15)=15\cdot15-15^2=0\)
Pinta-alan suurin arvo saavutetaan, kun
\(a=\frac{15}{2}=7{,}5\) ja
\(h=15-\frac{15}{2}=\frac{15}{2}=7{,}5\).
Vastaus: Sekä pituuden että leveyden tulee olla \(7{,}5\) metriä.
Huom. Pinta-alan lausekkeen suurin arvo välillä \(\left[0,15\right]\) voidaan määrittää GeoGebralla komennolla Max(a(15-a),0,15)Min().
4 RATIONAALIFUNKTIO
4.1 Tulon ja osamäärän derivoimissääntö
Derivoimissääntöjä
Olkoot \(f\) ja \(g\) derivoituvia funktioita.
- \(\text{D}\left(f(x)g(x)\right)=f'(x)g(x)+f(x)g'(x)\)
- \(\text{D}~\dfrac{f(x)}{g(x)}=\dfrac{{f}'(x)g(x)-f(x){g}'(x)}{{{(g(x))}^{2}}}\), kun \(g(x)\neq0\)
Esim. 1
Derivoi.
a) \((3x^4+2)(4-x^3)\)
b) \(\dfrac{2-x^3}{x^2+3}\)
Huom.
Potenssifunktion derivoimiskaava \(\text{D}~x^{n}=nx^{n-1}\) pätee myös negatiivisilla kokonaislukueksponenteilla. Tällöin \(x\neq0\).
Esim. 2
Derivoi.
a) \(\dfrac{1}{x^3}\)
b) \(\dfrac{4}{x^2}+\dfrac{x^3}{2}\)
4.2 Rationaalifunktion ääriarvot
Esim. 1
Määritä funktion \(f(x)=\dfrac{x^{3}}{x^{2}-1}\) ääriarvot.
Määritetään funktion \(f(x)=\dfrac{x^{3}}{x^{2}-1}\) määrittelyehto.
Nimittäjän nollakohdat:
\(\begin{align}x^{2}-1&=0\\x^{2}&=1 \quad \mid \sqrt{~}\\x&=\pm1\end{align}\)
Funktio \(f(x)=\dfrac{x^{3}}{x^{2}-1}\) on määritelty, kun \(x\neq\pm1\).
Derivoidaan.
\(\begin{align}f'(x)&=\dfrac{3x^{2}(x^{2}-1)-x^{3}\cdot2x}{(x^{2}-1)^{2}}\\ &=\dfrac{3x^{4}-3x^{2}-2x^{4}}{(x^{2}-1)^{2}}\\ &=\dfrac{x^{4}-3x^{2}}{(x^{2}-1)^{2}},\ x\neq\pm1 \end{align}\)
Derivaattafunktion nollakohdat:
\( \begin{align} f'(x)&=0\\ \dfrac{x^{4}-3x^{2}}{(x^{2}-1)^{2}}&=0\\ x^{4}-3x^{2}&=0\\ x^{2}(x^{2}-3)&=0 \end{align} \)
\(\begin{alignat}{2} x^{2}&=0&\quad\text{tai}\quad x^{2}-3&=0\\ x&=0& x^{2}&=3\quad\quad\mid\sqrt{~}\\ && x&=\pm\sqrt{3} \end{alignat}\)
Kulkukaavio
\( \begin{array}{lcccccccccc} &&-\sqrt{3}&&-1&&0&&1&&\sqrt{3}\\ f'(x)&+&\mid&-&\vdots&-&\mid&-&\vdots&-&\mid&+\\ f(x)&\nearrow&\mid&\searrow&\vdots&\searrow&\mid&\searrow&\vdots&\searrow&\mid&\nearrow\\ &&\text{max}&&\text{ei määr.}&&\text{terassi}&&\text{ei määr.}&&\text{min.}& \end{array} \)
Testipisteet
\(f'(-2)=\dfrac{(-2)^{4}-3\cdot(-2)^{2}}{((-2)^{2}-1)^{2}}=\dfrac{16-12}{(4-1)^{2}}\gt0\)
\(f'(-\sqrt{2})=\dfrac{(-\sqrt{2})^{4}-3\cdot(-\sqrt{2})^{2}}{((-\sqrt{2})^{2}-1)^{2}}=\dfrac{4-6}{(2-1)^{2}}\lt0\)
\(f'(-\frac{1}{2})=\dfrac{(-\frac{1}{2})^{4}-3\cdot(-\frac{1}{2})^{2}}{((-\frac{1}{2})^{2}-1)^{2}}=\dfrac{\frac{1}{16}-\frac{3}{4}}{(\frac{1}{4}-1)^{2}}\lt0\)
\(f'(\frac{1}{2})=\dfrac{(\frac{1}{2})^{4}-3\cdot(\frac{1}{2})^{2}}{((\frac{1}{2})^{2}-1)^{2}}=\dfrac{\frac{1}{16}-\frac{3}{4}}{(\frac{1}{4}-1)^{2}}\lt0\)
\(f'(\sqrt{2})=\dfrac{(\sqrt{2})^{4}-3\cdot(\sqrt{2})^{2}}{((\sqrt{2})^{2}-1)^{2}}=\dfrac{4-6}{(2-1)^{2}}\lt0\)
\(f'(2)=\dfrac{2^{4}-3\cdot2^{2}}{(2^{2}-1)^{2}}=\dfrac{16-12}{(4-1)^{2}}\gt0\)
Funktion maksimikohta on \(x=-\sqrt{3}\) ja sitä vastaava maksimiarvo \(f\left(-\sqrt{3}\right)=\dfrac{\left(-\sqrt{3}\right)^{3}}{\left(-\sqrt{3}\right)^{2}-1}=-\dfrac{3\sqrt{3}}{2}\).
Funktion minimikohta on \(x=\sqrt{3}\) ja sitä vastaava minimiarvo \(f\left(\sqrt{3}\right)=\dfrac{\left(\sqrt{3}\right)^{3}}{\left(\sqrt{3}\right)^{2}-1}=\dfrac{3\sqrt{3}}{2}\).
Vastaus: Minimiarvo on \(\dfrac{3\sqrt{3}}{2}\) ja maksimiarvo \(-\dfrac{3\sqrt{3}}{2}\).
4.3 Ääriarvotehtävä 2
Esim. 1
Kanalan seinustalle rakennetaan kanoille suorakulmion muotoinen pinta-alaltaan \(30\ \text{m}^2\) kokoinen aitaus, joka rajataan kolmelta sivulta verkkoaidalla. Kanalan seinusta on \(20\ \text{m}\) leveä. Mitkä ovat aitauksen mitat, kun verkkoaidan menekki on pienin mahdollinen? Kuinka paljon verkkoaitaa tarvitaan pienimmillään?
Mallikuva:

Aidan pituuden lauseke:
\(l=2x+y\)
Koska aitauksen pinta-ala on \(30\ \text{m}^2\), voidaan leveys \(x\) ilmaista pituuden \(y\) avulla:
\(\begin{align} xy&=30\\ x&=\dfrac{30}{y} \end{align}\)
Aidan pituuden lauseke saa muodon:
\(\begin{align} l&=2\cdot\dfrac{30}{y}+y\\ &=\dfrac{60}{y}+y \end{align}\)
Määrittelyehdot:
\(0\lt y\le20\quad\text{ja}\quad x\gt0\)
Määritetään aitauksen pituus funktiona \(l(y)\). Määritetään funktion \(l\) minimikohta ja minimiarvo välillä \(\left]0,20\right]\) GeoGebran CAS-laskimenMin()-komennolla.
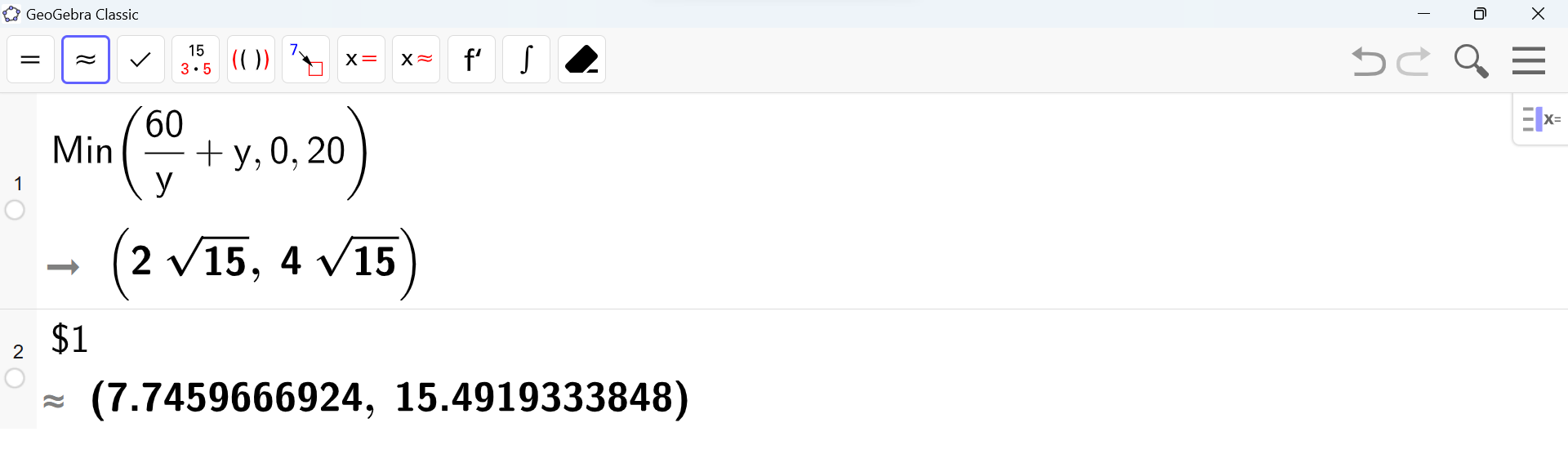
Minimikohta:
\(y=2\sqrt{15}=7{,}745\ldots\approx7{,}7\)
Minimiarvo:
\(l(2\sqrt{15})=15{,}491\ldots\approx15{,}5\)
Leveys \(x\):
\(x=\dfrac{30}{2\sqrt{15}}=\sqrt{15}=3{,}875\ldots\approx3{,}9\)
Vastaus: Aitauksen mitat ovat 3,9 m kertaa 7,7 m ja aidan pituus 15,5 m.
5 YHDISTETTY FUNKTIO
5.1 Yhdistetty funktio
Merkintä
Yhdistetty funktio merkitään $$f\ \circ\ g.$$ Luetaan "\(f\) pallo \(g\)".
Yhdistetty funktio
Olkoot \(f\) ja \(g\) funktioita. Tällöin yhdistetty funktio $$(f\ \circ\ g)(x)=f(g(x)).$$
Esim. 1
Olkoon \(f(x)=3x^2\) ja \(g(x)=2x-1\).
a) Muodosta \(f\ \circ\ g\) ja \(g\ \circ\ f\).
b) Laske \((f\ \circ\ g)(-1)\) ja \((g\ \circ\ f)(-1)\).
Huom.
- Jos \(f\) ja \(g\) ovat jatkuvia, myös \(f\ \circ\ g\) on jatkuva.
- Yhdistetyt funktiot ovat samat, jos kaikilla muuttujan eri arvoilla \(x\) yhdistettyjen funktioiden arvot ovat samat.
Huom.
GeoGebralla yhdistetyn funktion voi muodostaa määrittelemällä ensin ohjelmalle ulko- ja sisäfunktiot \(f\) ja \(g\) ja sitten käyttämällä komentoja f(g(x)) tai sievennä(f(g(x))) tai expand(f(g(x))).
5.2 Yhdistetyn funktion derivointi
Derivoimissääntöjä
-
Yhdistetyn funktion derivoimissääntö eli ketjusääntö:
Olkoon \(g\) kohdassa \(x\) derivoituva ja \(f\) kohdassa \(g(x)\) derivoituva funktio.
Tällöin
\((f\ \circ\ g)'(x)=\text{D}~f(g(x))=f'(g(x))\cdot g'(x)\).
Yhdistetyn funktion derivaatta lasketaan siis kertomalla ulkofunktion \(f\) derivaatta \(f'\) kohdassa \(g(x)\) sisäfunktion \(g\) derivaatalla \(g'\) kohdassa \(x\).
Esim. 1
Derivoi \(f(x)=(x^{2}-1)^{5}\).
\( \begin{align} f'(x)&=5(x^{2}-1)^{4}\cdot2x\\ &=10x(x^{2}-1)^{4} \end{align} \)
Esim. 2
Derivoi \(f(x)=\dfrac{1}{(3x^{2}+4x)^{3}}\).
Määrittelyehto
Nimittäjän nollakohdat:
\( \begin{align} (3x^{2}+4x)^{3}&=0 \quad \mid \sqrt[3]{~}\\ 3x^{2}+4x&=0\\ x(3x+4)&=0 \end{align} \)
\(\begin{alignat}{2} x&=0&\quad\text{tai}\quad 3x+4&=0\\ && x&=-\dfrac{4}{3} \end{alignat}\)
Funktio \(f\) on määritelty, kun \(x\neq-\dfrac{4}{3}\) tai \(x\neq0\).
Muutetaan funktio \(f\) potenssimuotoon.
\(f(x)=\dfrac{1}{(3x^{2}+4x)^{3}}=(3x^{2}+4x)^{-3}\).
Derivoidaan ulkofunktiota potenssifunktion derivoimiskaavalla.
\( \begin{align} f'(x)&=-3(3x^{2}+4x)^{-4}\cdot(6x+4)\\ &=(-18x-12)\cdot\dfrac{1}{(3x^{2}+4x)^{4}}\\ &=-\dfrac{18x+12}{(3x^{2}+4x)^{4}}, \ \text{kun}\ x\neq-\dfrac{4}{3}\ \text{tai}\ x\neq0 \end{align} \)
Esim. 3
Olkoon funktio \(f(x)=4x^{2}(2x^{3}+x^2)^{6}\).
a) Derivoi funktio \(f\).
b) Määritä derivaattafunktion \(f'\) nollakohdat.
a) Derivoidaan funktio käyttäen tulon derivoimissääntöä ja ketjusääntöä.
\( \begin{align} f'(x)&=\text{D}~4x^{2}\cdot(2x^{3}+x^{2})^{6}+4x^{2}\cdot\text{D}~(2x^{3}+x^{2})^{6}\\ &=8x(2x^{3}+x^{2})^{6}+4x^{2}\cdot6(2x^{3}+x^{2})^{5}\cdot(6x^2+2x)\\ &=8x(2x^{3}+x^{2})^{5}\left[(2x^{3}+x^{2})+3x(6x^2+2x)\right]\\ &=8x(2x^{3}+x^{2})^{5}\left(2x^{3}+x^{2}+18x^3+6x^2\right)\\ &=8x(2x^{3}+x^{2})^{5}\left(20x^{3}+7x^{2}\right)\\ &=8x^{3}(2x^{3}+x^{2})^{5}\left(20x+7\right)\\ \end{align} \)b) Määritetään derivaattafunktion nollakohdat tulon nollasäännön avulla.
\(\begin{align} f'(x)&=0\\ 8x^{3}(2x^{3}+x^{2})^{5}\left(20x+7\right)&=0\\ \end{align} \)Tulon nollasääntö:
\(\begin{align} 8x^{3}&=0\\ x&=0\\ \end{align} \)
tai
\(\begin{align} (2x^{3}+x^{2})^{5}&=0 \quad \mid \sqrt[5]{~}\\ 2x^{3}+x^{2}&=0\\ x^{2}(2x+1)&=0 \end{align} \)
\(\begin{alignat}{2} x^{2}&=0&\quad\text{tai}\quad 2x+1&=0\\ x&=0& x&=-\dfrac{1}{2} \end{alignat}\)
tai
\(\begin{align} 20x+7&=0\\ x&=-\dfrac{7}{20}\\ \end{align} \)
Vastaus: \(x=-\dfrac{1}{2}\), \(x=-\dfrac{7}{20}\) ja \(x=0\)
6 JUURIFUNKTIO
6.1 Juurifunktion derivointi
Juurifunktio derivoidaan käyttäen potenssifunktion derivoimiskaavaa $$\text{D}~x^{n}=nx^{n-1}.$$
Esim. 1
Derivoi.
a) \(\sqrt{x},\ \text{kun}\ x\gt0\) b) \(\sqrt[3]{x^{2}},\ \text{kun}\ x\neq0.\)
a)
\(\begin{align} \text{D}\,\sqrt{x}&=\text{D}\,x^{\frac{1}{2}}\\ &=\dfrac{1}{2}x^{-\frac{1}{2}}\\ &=\dfrac{1}{2\sqrt{x}},\ \text{kun}\ x\neq0 \end{align}\)
b)
\(\begin{align} \text{D}\,\sqrt[3]{x^{2}}&=\text{D}\,x^{\frac{2}{3}}\\ &=\dfrac{2}{3}x^{-\frac{1}{3}}\\ &=\dfrac{2}{3\sqrt[3]{x}},\ \text{kun}\ x\gt0 \end{align}\)
Esim. 2
Derivoi.
a) \(f(x)=(3x+2)\sqrt{3x+2},\ \text{kun}\ x\ge-\frac{2}{3}\).
b) \(g(x)=\dfrac{3x+2}{\sqrt{3x+2}},\ \text{kun}\ x\gt-\frac{2}{3}\).
Esim. 3
Derivoi \(f(x)=\sqrt{x^{3}+1}\).
6.2 Juurifunktion ääriarvot
Esim. 1
Määritä derivaatan avulla pisteen \((0,4)\) pienin etäisyys paraabelista \(y=-x^{2}+9\).
Merkitään paraabelin pistettä \((x,y)\).
Muodostetaan lauseke pisteiden \((0,4)\) ja \((x,y)\) väliselle etäisyydelle ja määritellään se funktiona.
\(\begin{align} d(x)&=\sqrt{(x-0)^{2}+(y-4)^{2}}\quad\mid y=-x^{2}+9\\ &=\sqrt{x^{2}+(-x^{2}+9-4)^{2}}\\ &=\sqrt{x^{2}+(-x^{2}+5)^{2}} \end{align}\)
Määrittelyehto:
Koska \(x^{2}\ge0\) ja \((-x^{2}+5)^{2}\ge0\) aina, niin \(x^{2}+(-x^{2}+5)^{2}\ge0\).
Funktio \(d\) on määritelty kaikilla reaaliluvuilla \(x\).
Derivoidaan.
\(\begin{align} d'(x)&=\text{D}\sqrt{x^{2}+(-x^{2}+5)^{2}}\\ &=\text{D}\left(x^{2}+(-x^{2}+5)^{2}\right)^{\frac{1}{2}}\\ &=\frac{1}{2}\left(x^{2}+(-x^{2}+5)^{2}\right)^{-\frac{1}{2}}\left(2x+2(-x^{2}+5)(-2x)\right)\\ &=\dfrac{x+2x^{3}-10x}{\sqrt{x^{2}+(-x^{2}+5)^{2}}}\\ &=\dfrac{2x^{3}-9x}{\sqrt{x^{2}+(-x^{2}+5)^{2}}}\quad\quad\left(,\ x^{2}+(-x^{2}+5)^{2}\gt0\right) \end{align}\)
Derivaattafunktion nollakohdat:
\(\begin{align} d'(x)&=0\\ \dfrac{2x^{3}-9x}{\sqrt{x^{2}+(-x^{2}+5)^{2}}}&=0\\ 2x^{3}-9x&=0\\ x(2x^{2}-9)&=0\\ x=0\quad \text{tai}\quad2x^{2}-9&=0\\ 2x^{2}&=9\\ x^{2}&=\dfrac{9}{2}\\ x&=\pm\dfrac{3}{\sqrt{2}} \end{align}\)
Kulkukaavio:
\(\begin{matrix} & &-\frac{3}{\sqrt{2}}& &0 & &\frac{3}{\sqrt{2}}&\\ \hline d'(x)&- &\mid &+&\mid&-&\mid &+\ \\ \hline d(x) &\searrow&\mid &\nearrow&\mid&\searrow&\mid&\nearrow\ \\ \hline &&\text{min}&&\text{max}&&\text{min}& \end{matrix}\)
Testipisteet:
\(d'\left(-3\right)=\dfrac{-27}{5}\lt0\)
\(d'\left(-1\right)=\dfrac{7}{\sqrt{17}}\gt0\)
\(d'\left(1\right)=\dfrac{-7}{\sqrt{17}}\lt0\)
\(d'\left(3\right)=\dfrac{27}{5}\gt0\)
Funktio \(d\) saa pienimmän arvonsa kohdassa \(-\frac{3}{\sqrt{2}}\) tai kohdassa \(\frac{3}{\sqrt{2}}\). Lasketaan funktion arvot näissä kohdissa.
\(d\left(-\dfrac{3}{\sqrt{2}}\right)=\dfrac{\sqrt{19}}{2}\)
\(d\left(\dfrac{3}{\sqrt{2}}\right)=\dfrac{\sqrt{19}}{2}\)
Vastaus: Pisteen \((0,4)\) pienin etäisyys paraabelista \(y=-x^{2}+9\) on \(\frac{\sqrt{19}}{2}\) ja se saavutetaan, kun \(x=-\frac{3}{\sqrt{2}}\) ja \(x=\frac{3}{\sqrt{2}}\).
7 TRIGONOMETRISET FUNKTIOT
7.1 Sini- ja kosinifunktion derivointi
Derivoimiskaavoja
\(\text{D}~\sin x=\cos x\)
\(\text{D}~\cos x=-\sin x\)
Esim. 1
Derivoi.
a) \(2\sin x\) b) \(\cos 2x\) c) \(\sin x^{2}\)
a) \(\text{D}(2\sin x)\)
\(\quad=2\cdot\text{D}\sin x\)
\(\quad=2\cos x\)
b) \(\text{D}(\cos 2x)\)
\(\quad=-\sin 2x\cdot\text{D}2x\)
\(\quad=-\sin 2x\cdot2\)
\(\quad=-2\sin 2x\)
c) \(\text{D}(\sin x^{2})\)
\(\quad=\cos x^{2}\cdot\text{D}x^{2}\)
\(\quad=\cos x^{2}\cdot2x\)
\(\quad=2x\cos x^{2}\)
Esim. 2
Derivoi.
a) \(\cos^{2} x\) b) \(\sin^{3} x\)
a) \(\text{D}\cos^{2} x\)
\(\quad=\text{D}(\cos x)^{2}\)
\(\quad=2(\cos x)\cdot\text{D}\cos x\)
\(\quad=2(\cos x)\cdot(-\sin x)\)
\(\quad=-2\sin x\cos x\)
b) \(\text{D}\sin^{3} x\)
\(\quad=\text{D}(\sin x)^{3}\)
\(\quad=3(\sin x)^{2}\cdot\text{D}\sin x\)
\(\quad=3(\sin x)^{2}\cdot\cos x\)
\(\quad=3\sin^{2}x\cos x\)
Esim. 3
Määritä funktion \(f\) derivaattafunktion nollakohdat.
a) \(f(x)=x-\sin 2x\) b) \(f(x)=2x-4\cos \frac{x}{2}\)
a) Derivoidaan.
\(\begin{align} \quad f'(x)&=\text{D}x-\text{D}(\sin 2x)\\ &=1-\cos 2x\cdot\text{D}2x\\ &=1-\cos 2x\cdot2\\ &=1-2\cos 2x \end{align}\)
Derivaattafunktion nollakohdat:
\(\begin{align} f'(x)&=0\\ \quad1-2\cos 2x&=0\\ -2\cos 2x&=-1\quad\mid\,:(-2)\\ \cos 2x&=\frac{1}{2}\ \quad\mid\arccos\\ 2x&=\pm\frac{\pi}{3}+n\cdot2\pi\ \ \mid\cdot\,\frac{1}{2}\\ x&=\pm\frac{\pi}{6}+n\pi\ (n\in\mathbb{Z}) \end{align}\)
Vastaus: \(x=\pm\dfrac{\pi}{6}+n\pi,\ n\in\mathbb{Z}\).
b) Derivoidaan.
\(\begin{align} \quad f'(x)&=\text{D}2x-\text{D}(4\cos \frac{x}{2})\\ &=2-4\cdot \text{D}\cos\frac{x}{2}\\ &=2-4\cdot(-\sin\frac{x}{2})\cdot\text{D}\frac{x}{2}\\ &=2-4\cdot(-\sin\frac{x}{2})\cdot\frac{1}{2}\\ &=2+2\sin\frac{x}{2} \end{align}\)
Derivaattafunktion nollakohdat:
\(\begin{align} f'(x)&=0\\ \quad2+2\sin\frac{x}{2}&=0\\ 2\sin\frac{x}{2}&=-2\quad\mid\,:2\\ \sin\frac{x}{2}&=-1\quad\mid\arcsin\\ \frac{x}{2}&=\frac{3\pi}{2}+n\cdot2\pi\ \ \mid\cdot\,2\\ x&=3\pi+n\cdot4\pi\\ \text{tai}\\ \frac{x}{2}&=\pi-\frac{3\pi}{2}+n\cdot2\pi\\ \frac{x}{2}&=\frac{\pi}{2}+n\cdot2\pi\ \ \mid\cdot\,2\\ x&=-\pi+n\cdot4\pi\ (n\in\mathbb{Z}) \end{align}\)
Yhdistettynä \(x=3\pi+n\cdot4\pi,\ n\in\mathbb{Z}\).
Vastaus: \(x=3\pi+n\cdot4\pi,\ n\in\mathbb{Z}\).
7.2 Sini- ja kosinifunktion ääriarvot
Koska sini- ja kosinifunktiot ovat jaksollisia, voidaan tarkastelu rajoittaa yhden perusjakson mittaiseen väliin. Sini- ja kosinifunktion suurin ja pienin arvo löytyvät perusjakson mittaiselta väliltä.
Perusjakson määrittäminen
Muotoa \(\sin bx\) ja \(\cos bx\) olevien sini- ja kosinifunktioiden perusjakso on $$\dfrac{2\pi}{b}.$$
Esim. 1
Määritä funktion \(f(x)=2\sin x+\cos2x\) suurin ja pienin arvo.
Funktion \(\sin x\) perusjakso on \(2x\).
Funktion \(\cos2x\) perusjakso on \(\frac{2\pi}{2}=\pi\).
Luku \(\pi\) sisältyy jaksoon \(2\pi\) tasan kaksi kertaa. Siten funktion \(f\) arvot toistuvat jakson \(2\pi\) välein ja funktio \(f\) saa kaikki arvonsa välillä \(\left[0,2\pi\right]\).
Funktio \(f\) on välillä \(\left[0,2\pi\right]\) määritelty ja jatkuva. Siten se saa myös suurimman ja pienimmän arvonsa välin päätepisteessä tai välille kuuluvassa derivaattafunktion nollakohdassa.
Derivoidaan.
\(\begin{align} f'(x)&=2\cos x-\sin2x\cdot2\\ &=2\cos x-2\sin2x \end{align}\)
Derivaattafunktion nollakohdat:
\(\begin{align} f'(x)&=0\\ 2\cos x-2\sin2x&=0\\ 2\cos x&=2\sin2x\quad\ \mid\,:2\\ \cos x&=\sin2x\quad\ \ \ \mid\cos x=\sin\left(\frac{\pi}{2}-x\right)\\ \sin\left(\dfrac{\pi}{2}-x\right)&=\sin2x\quad\quad\mid\arcsin\\ \dfrac{\pi}{2}-x&=2x+n\cdot2\pi\\ -x+2x&=-\dfrac{\pi}{2}+n\cdot2\pi\\ -3x&=-\dfrac{\pi}{2}+n\cdot2\pi\ \mid\cdot\left(-\frac{1}{3}\right)\\ x&=\dfrac{\pi}{6}-n\cdot\dfrac{2}{3}\pi\\ &\text{tai}\\ \dfrac{\pi}{2}-x&=\pi-2x+n\cdot2\pi\\ -x+2x&=\pi-\dfrac{\pi}{2}+n\cdot2\pi\\ x&=\dfrac{\pi}{2}+n\cdot2\pi\quad(n\in\mathbb{Z}) \end{align}\)
Väliin \(\left[0,2\pi\right]\) kuuluvat \(\frac{\pi}{6}\), \(\frac{\pi}{2}\), \(\frac{5}{6}\pi\) ja \(\frac{3}{2}\pi\).
Lasketaan funktion \(f\) arvot välin päätepisteissä ja välille kuuluvissa derivaatan nollakohdissa.
\(\begin{align} f\left(0\right)&=2\sin 0+\cos(2\cdot0)\\ &=0+1=1 \end{align}\)
\(\begin{align} f\left(\frac{\pi}{6}\right)&=2\sin \frac{\pi}{6}+\cos\left(2\cdot\frac{\pi}{6}\right)\\ &=2\cdot\frac{1}{2}+\frac{1}{2}=\frac{3}{2}\quad\text{suurin} \end{align}\)
\(\begin{align} f\left(\frac{\pi}{2}\right)&=2\sin \frac{\pi}{2}+\cos\left(2\cdot\frac{\pi}{2}\right)\\ &=2\cdot1+(-1)=1 \end{align}\)
\(\begin{align} f\left(\frac{5\pi}{6}\right)&=2\sin \frac{5\pi}{6}+\cos\left(2\cdot\frac{5\pi}{6}\right)\\ &=2\cdot\frac{1}{2}+\frac{1}{2}=\frac{3}{2}\quad\text{suurin} \end{align}\)
\(\begin{align} f\left(\frac{3\pi}{2}\right)&=2\sin \frac{3\pi}{2}+\cos\left(2\cdot\frac{3\pi}{2}\right)\\ &=2\cdot(-1)+(-1)=-3\quad\text{pienin} \end{align}\)
\(\begin{align} f\left(2\pi\right)&=2\sin 2\pi+\cos(2\cdot2\pi)\\ &=0+1=1 \end{align}\)
Koska välillä \(\left[0,2\pi\right]\) funktion \(f\) suurin arvo on \(\frac{3}{2}\) ja pienin arvo \(-3\), ne ovat myös funktion suurin ja pienin arvo koko reaalilukuvälillä.
Vastaus: Suurin arvo on \(\frac{3}{2}\) ja pienin arvo \(-3\).
7.3 Ääriarvotehtävä 3
Esim. 1
Määritä puolisuunnikkaan suurin mahdollinen pinta-ala.
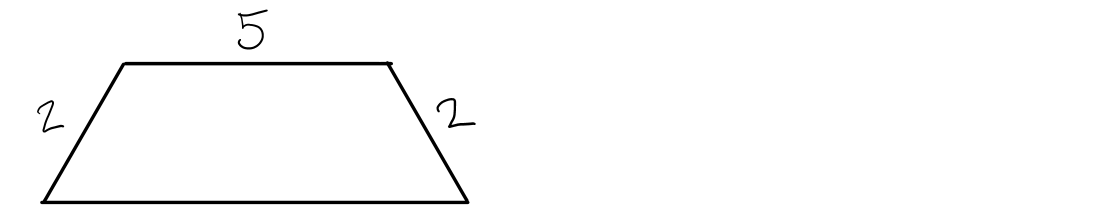
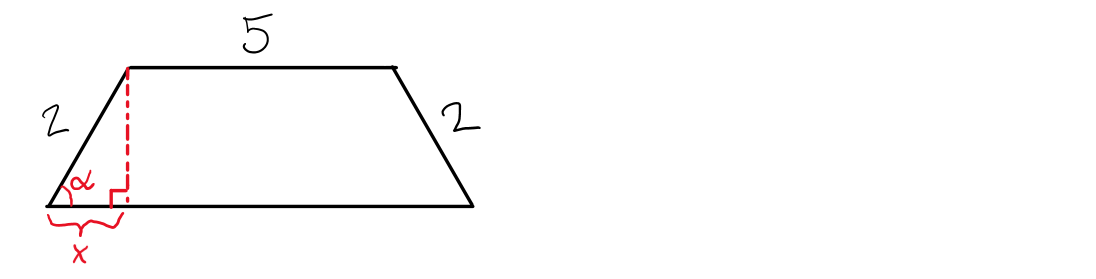
Määritetään \(x\).
\(\begin{align} \cos\alpha&=\dfrac{x}{2}\\ x&=2\cos\alpha \end{align}\)
Määritetään kannan pituus.
\(\begin{align} a&=5+2x\\ &=5+2\cdot2\cos\alpha\\ &=5+4\cos\alpha \end{align}\)
Määritetään korkeus.
\(\begin{align} \sin\alpha&=\dfrac{h}{2}\\ h&=2\sin\alpha \end{align}\)
Määritetään puolisuunnikkaan pinta-alan lauseke.
\(A=\frac{1}{2}\left(a+b\right)h\)
\(\begin{align} A&=\frac{1}{2}\left(5+4\cos\alpha+5\right)2\sin\alpha\\ &=10\sin\alpha+4\cos\alpha\sin\alpha \end{align}\)
Kulma \(\alpha\) on välillä \(\left[0,\frac{\pi}{2}\right]\).
Käytetään GeoGebran CAS-laskimen Max()-komentoa pinta-alan suurimman arvon määrittämiseen välillä \(\left[0,\frac{\pi}{2}\right]\).
\(A=10{,}686\ldots\approx10{,}7\).
Vastaus: \(10{,}7\).
8 EKSPONENTTI- JA LOGARITMIFUNKTIO
8.1 Neperin luku
Kertaus: Eksponenttifunktio
Eksponenttifunktio on muotoa
$$f(x)=a^{x},$$
missä \(a\gt0\) ja \(a\neq0\).
Neperin luku
Neperin luku \(e\) on reaaliluku, jonka eksponenttifunktion \(e^{x}\) derivaatta kohdassa 0 on 1.
Neperin luku on päättymätön, jaksoton desimaaliluku.
\(e=2{,}718281\ldots\approx2{,}72\).
Esim. 1
Ratkaise yhtälö \(e^{x}=7\).
\(\begin{align} e^{x}&=7\quad\mid \log_{e}\ \text{eli}\ \ln\\ \ln e^{x}&=\ln 7\\ x&=\ln 7=1{,}9459\ldots\approx1{,}95 \end{align}\)
8.2 Eksponenttifunktion derivointi
Derivoimiskaavoja
\(\text{D}~e^{x}=e^{x}\)
\(\text{D}~a^{x}=a^{x}\ln a,\ \text{kun}\ a\gt0.\)
Esim. 1
Derivoi.
a) \(5e^{x}+7\) b) \(-2^{x}\)
a) \(\text{D}(5e^{x}+7)\)
\(=5\cdot\text{D}e^{x}+\text{D}7\)
\(=5e^{x}\)
b) \(\text{D}(-2^{x})\)
\(=-1\cdot\text{D}2^{x}\)
\(=-1\cdot2^{x}\cdot\ln2\)
\(=-2^{x}\ln2\)
Esim. 2
Derivoi.
a) \(e^{x^{2}+7}\) b) \(5^{-2x}\)
a) \(\text{D}(e^{x^{2}+7})\quad\mid \text{D}f(g(x))=f'(g(x))\cdot g'(x)\)
\(=e^{x^{2}+7}\cdot\text{D}(x^{2}+7)\)
\(=e^{x^{2}+7}\cdot2x\)
\(=2xe^{x^{2}+7}\)
b) \(\text{D}(5^{-2x})\quad\mid \text{D}f(g(x))=f'(g(x))\cdot g'(x)\)\)
\(=5^{-2x}\cdot\ln 5\cdot\text{D}(-2x)\)
\(=5^{-2x}\cdot\ln 5\cdot(-2)\)
\(=-5^{-2x}\cdot2\ln 5\)
8.3 Logaritmifunktion derivointi
Kertausta
Logaritmin määritelmä
$$\log_{a}x=y\quad\Longleftrightarrow\quad a^{y}=x$$
Esim. 1
Ratkaise yhtälö.
a) \(\ln 2x=1\) b) \(\log_{3}(x+1)=2\)
Derivoimiskaavoja
\(\text{D}~\ln x=\frac{1}{x},\ \text{kun}\ x\gt0.\)
\(\text{D}~\log_{a} x=\frac{1}{x\ln a},\ \text{kun}\ a\gt0,\ a\neq1\ \text{ja}\ x\gt0.\)
Esim. 2
Derivoi.
a) \(3\ln x\) b) \(\ln 3x\) c) \(\ln \frac{x}{3}\) d) \(\ln \frac{3}{x}\) e) \(\ln x^{3}\)
Esim. 3
Derivoi.
a) \(\log_{3} x\) b) \(\lg x^{3}\)
8.4 Sovelluksia
Esim. 1
Cesium-134:n puoliintumisaika on 2 vuotta.
Oletetaan, että Tsernobylin ydinvoimalaonnettomuudessa vuonna 1986 vapautui \(m_0\) määrä Cesium-134:ää.
a) Määritä funktio \(m(t)\), joka kuvaa jäljellä olevan Cesium-134:n määrää, kun \(t\) on aika vuosina onnettomuudesta.
b) Millä nopeudella Cesium-134:n määrä väheni vuonna 1990? Entä 2025?
a) Puoliintumisaika on aika, jonka kuluttua jäljellä on puolet alkuperäisestä määrästä radioaktiivista ainetta.
Jäljellä olevan aineen määrä, kun on kulunut...
1. puoliintumisaika \(m_0\cdot0{,}5\)
2. puoliintumisaika \(m_0\cdot0{,}5\cdot0{,}5\)
3. puoliintumisaika \(m_0\cdot0{,}5\cdot0{,}5\cdot0{,}5\)
...
n. puoliintumisaika \(m_0\cdot0{,}5^{n}\)
Kun puoliintumisaika on 2 vuotta, niin \(n=\frac{1}{2}t\), missä \(t\) on aika vuosina.
Määrä ajan funktiona voidaan ilmaista:
\(m(t)=m_0\cdot0{,}5^{\frac{1}{2}t}\).
Vastaus: \(m(t)=m_0\cdot0{,}5^{\frac{1}{2}t}\).
b) Funktion derivaatta on funktion muutosnopeus.
Derivoidaan.
\(m'(t)=m_0\cdot0{,}5^{\frac{1}{2}t}\ln0{,}5\cdot\frac{1}{2}\).
Vuonna 1990:
\(1990-1986=4\)
\(m'(4)=-\frac{1}{8}\ln 2\ m_0\)
Vastaus: \(-\frac{1}{8}\ln2\ m_0\)/vuodessa
Vuonna 2025:
\(2026-1986=40\)
\(m'(40)=-\frac{1}{2097152}\ln2 m_{0}\)
Vastaus: \(-\frac{1}{2097152}\ln2 m_{0}\)/vuodessa