3D-geometria (MAA10)
Laajuus
2 op
Yleiset tavoitteet (LOPS 2021)
Moduulin tavoitteena on, että opiskelija
- syventää vektorilaskennan tuntemustaan ja oppii käyttämään vektoreita kolmiulotteisessa avaruudessa
- oppii tutkimaan xyz-koordinaatiston pisteitä, suoria ja tasoja vektoreiden avulla
- vahvistaa avaruusgeometrian osaamistaan ääriarvosovellusten yhteydessä
- tutustuu kahden muuttujan funktioon
- osaa käyttää ohjelmistoja vektoreiden, suorien, tasojen ja pintojen havainnollistamisessa sekä vektorilaskennassa.
Keskeiset sisällöt (LOPS 2021)
- vektoriesitys kolmiulotteisessa koordinaatistossa
- piste- ja ristitulo
- piste, suora ja taso avaruudessa
- kulma avaruudessa
- yhden muuttujan differentiaali- ja integraalilaskennan sovelluksia avaruusgeometriassa
- kahden muuttujan funktio ja pinta avaruudessa
Aikataulu
Suoritus
- osallistuminen
- tehtävien tekeminen
- monivalintatehtävien tekeminen
- loppukoe
Arviointi
- säännöllinen, aktiivinen ja vastuullinen osallistuminen +1 p
- tehtävien asianmukainen ja jatkuva tekeminen +1 p
- monivalintatehtävistä +1 p kustakin tehdystä monivalintakokonaisuudesta, saavutettava tavoitetaso 80 %, yht. max. 4 p
- loppukokeesta max. 56 p
- max. 60 p (teoreettisesti 62 p)
- 30 % arviointi
| Pisteet | Arvosana | Muuta |
|---|---|---|
| 0 - 9 | i \(\rightarrow\) K | Pakko täydentää. |
| 10 - 17 | i \(\rightarrow\) 4 | Oikeus täydentää. |
| 18 - 25 | 5 | |
| 26 - 33 | 6 | |
| 34 - 41 | 7 | |
| 42 - 49 | 8 | |
| 50 - 57 | 9 | |
| 58 - 60 | 10 |
Keskeyttäminen
Opettaja keskeyttää opiskelijan opintojakson, jos
- opiskelija niin pyytää
- opiskelija ei ole läsnä opintojakson kahdella ensimmäisellä opetuskerralla ja opiskelija ei ole yhteydessä opettajaan eikä opettaja saa yhteyttä opiskelijaan.
Opettaja voi keskeyttää opiskelijan opintojakson, jos opiskelijalla on neljä poissaoloa. Tällaiset tilanteet opettaja käy läpi tapauskohtaisesti ja on ennen lopullista keskeytystä yhteydessä opiskelijaan.
Keskeyttämisestä opettaja merkitsee opintojaksosta opiskelijalle K-merkinnän Wilmaan ja poistaa opiskelijan sen jälkeen Wilman ryhmästä. Opettaja lähettää keskeyttämisestä viestin opiskelijalle, alaikäisen opiskelijan huoltajalle, ryhmänohjaajalle ja opolle.
1 VEKTORIT AVARUUDESSA
1.1 Vektori xyz-koordinaatistossa
Tason xy-koordinaatisto voidaan laajentaa kolmiulotteisen avaruuden koordinaatistoksi lisäämällä x- ja y-akseleita vastaan kohtisuorassa oleva z-akseli.
Näin saatava koordinaatisto esitetään yleensä niin sanotusti oikeakätisesti siten, että x-akselin positiivinen suunta osoittaa kohti katsojaa, y-akselin positiivinen suunta oikealle ja z-akselin positiivinen suunta ylöspäin.
Yleisesti kolmiulotteisen avaruuden kantavektoreiksi voidaan valita mitkä tahansa kolme vektoria, jotka eivät ole samassa tasossa.
Kantavektorit \(\bar{i}\), \(\bar{j}\) ja \(\bar{k}\)
Erityisesti xyz-koordinaatiston kantavektoreina käytetään x-, y- ja z-akseleiden suuntaisia yksikkövektoreita \(\bar{i}\), \(\bar{j}\) ja \(\bar{k}\), missä siis \(\bar{i}\perp\bar{j}\), \(\bar{i}\perp\bar{k}\) ja \(\bar{j}\perp\bar{k}\).
Komponenttiesitys
Mikä tahansa xyz-koordinaatiston vektori voidaan esittää komponenttimuodossa \(\bar{a}=a_{x}\bar{i}+a_{y}\bar{j}+a_{z}\bar{k}\), missä \(a_{x}\), \(a_{y}\) ja \(a_{z}\) ovat x-, y- ja z-akseleiden suuntaisten komponenttien kertoimet.
Paikkavektori
Pisteen \(P\) paikkavektori \(\overline{OP}\) on vektori, joka alkaa origosta \(O\) ja päättyy pisteeseen \(P\).
Pisteen \(P\) paikkavektori on $$\overline{OP}=x\bar{i}+y\bar{j}+z\bar{k},$$ missä \((x,y,z)\) ovat pisteen \(P\) koordinaatit.
Esim. 1
Määritä pisteen \(P=(3,-2,4)\) paikkavektori.
Avaruuden vektorin pituus vastaa suorakulmaisen särmiön avaruuslävistäjän pituutta.
Lause
Suorakulmaisen särmiön avaruuslävistäjän pituuden neliö on särmien pituuksien neliöiden summa. $$d^2=a^2+b^2+c^2.$$
Vektorin pituus
Vektorin \(\bar{a}=a_{x}\bar{i}+a_{y}\bar{j}+a_{z}\bar{k}\) pituus on $$\left|\bar{a}\right|=\sqrt{a_{x}^2+a_{y}^2+a_{z}^2}.$$
Esim. 2
Määritä pisteen \(P=(3,-2,4)\) paikkavektorin pituus.
Esim. 3
Olkoon pisteen \(A\) paikkavektori \(\overline{OA}=-2\bar{i}+\bar{j}+3\bar{k}\) ja pisteiden \(A\) ja \(B\) välinen vektori \(\overline{AB}=4\bar{i}-5\bar{j}-2\bar{k}\). Määritä pisteiden \(A\) ja \(B\) koordinaatit.
1.2 Kahden pisteen välinen vektori
Kahden pisteen välinen vektori
Pisteiden \(A=(a_{x},a_{y},a_{z})\) ja \(B=(b_{x},b_{y},b_{z})\) välinen vektori:$$\overline{AB}=(b_x-a_x)\bar{i}+(b_y-a_y)\bar{j}+(b_z-a_z)\bar{k}.$$
Esim. 1
Määritä pisteiden \(A=(1,2,-3)\) ja \(B=(6,-5,4)\) välinen vektori.
Vastaus: \(\overline{AB}=5\bar{i}-7\bar{j}+7\bar{k}\).
Kahden pisteen välisen vektorin pituus
Vektorin \(\overline{AB}\) pituus on pisteiden \(A=(a_{x},a_{y},a_{z})\) ja \(B=(b_{x},b_{y},b_{z})\) välinen etäisyys:$$\left|\overline{AB}\right|=\sqrt{(b_x-a_x)^2+(b_y-a_y)^2+(b_z-a_z)^2}.$$
Esim. 2
Määritä pisteiden \(A=(1,2,-3)\) ja \(B=(6,-5,4)\) välisen vektorin pituus.
Vastaus: \(\left|\overline{AB}\right|=\sqrt{123}\).
1.3 Yksikkövektori
Yksikkövektori
Vektorin \(\bar{a}\) suuntainen yksikkövektori: $$\bar{a}^{0}=\frac{1}{\left|\bar{a}\right|}\bar{a}=\frac{\bar{a}}{\left|\bar{a}\right|}.$$
Esim. 1
Määritä vektorin \(\bar{a}=4\bar{i}+3\bar{j}-\bar{k}\) suuntainen yksikkövektori.
Vastaus: \(\bar{a}^{0}=\frac{4}{\sqrt{26}}\bar{i}+\frac{3}{\sqrt{26}}\bar{j}-\frac{1}{\sqrt{26}}\bar{k}\).
Esim. 2
Pisteestä \(P=(-7,6,8)\) siirrytään \(6\) yksikköä vektorin \(\bar{a}=2\bar{i}-\bar{j}+2\bar{k}\) suuntaan. Mihin pisteeseen päädytään?
Vastaus: \((-3,4,12)\).
Huom.
GeoGebralla vaikkapa vektorin \(\bar{a}=3\bar{i}-4\bar{j}+2\bar{k}\) suuntainen yksikkövektori voidaan määrittää komennolla Yksikkövektori((3,-4,2)).
1.4 Yhdensuuntaiset vektorit
Vektorien yhdensuuntaisuus
Vektorit \(\bar{a}\) ja \(\bar{b}\) ovat yhdensuuntaiset, jos ja vain jos vektori \(\bar{a}\) saadaan vektorista \(\bar{b}\) kertomalla nollasta eroavalla reaaliluvulla \(t\) eli $$\bar{a}\parallel\bar{b}\quad\Leftrightarrow\quad\bar{a}=t\bar{b}, t\neq0.$$
Esim. 1
Ovatko vektorit \(\bar{a}=2\bar{i}-4\bar{j}+8\bar{k}\) ja \(\bar{b}=-3\bar{i}+6\bar{j}-12\bar{k}\) yhdensuuntaiset?
Vastaus: Kyllä, koska on olemassa \(t=-\frac{2}{3}\), jolle pätee \(\bar{a}=-\frac{2}{3}\bar{b}\).
1.5 Vektorin komponentit
Yleensä xyz-koordinaatistossa kantavektoreiksi valitaan koordinaattiakselien suuntaiset yksikkövektorit \(\bar{i}\), \(\bar{j}\) ja \(\bar{k}\). Kantavektoreiksi voitaisiin kuitenkin valita mitkä tahansa erisuuntaiset avaruuden vektorit \(\bar{u}\), \(\bar{v}\) ja \(\bar{w} \), joista kolmas ei ole samassa tasossa kahden muun kanssa.
Jokainen avaruuden vektori \(\bar{a}\) voitaisiin tällöin ilmaista komponenttien \(r\bar{u}\), \(s\bar{v}\) ja \(t\bar{w} \) summana $$\bar{a}=r\bar{u}+s\bar{v}+t\bar{w},$$ missä \(r\), \(s\) ja \(t\) ovat reaalilukukertoimia.
Vektorin komponenttiesityksen yksikäsitteisyys
Olkoot \(\bar{u}\), \(\bar{v}\) ja \(\bar{w}\) kolme erisuuntaista 3-ulotteisen avaruuden vektoria, joista kolmas ei ole samassa tasossa kahden muun kanssa.
Olkoot \(a\), \(b\), \(c\), \(r\), \(s\) ja \(t\) reaalilukuja.
Jos \(a\bar{u}+b\bar{v}+c\bar{w}=r\bar{u}+s\bar{v}+t\bar{w}\), niin tällöin välttämättä \(a=r\), \(b=s\) ja \(c=t\).
Esim. 1
Millä vakion \(t\) arvoilla vektorit \(\bar{a}=2\bar{i}-\bar{j}+(t-1)\bar{k}\) ja \(\bar{b}=-10\bar{i}+t\bar{j}-20\bar{k}\) ovat yhdensuuntaiset?
Esim. 2
Jaa vektori \(\bar{a}=3\bar{i}-7\bar{j}+5\bar{k}\) vektoreiden \(\bar{u}=\bar{i}\), \(\bar{v}=\bar{i}-\bar{j}\) ja \(\bar{w}=\bar{j}+\bar{k}\) suuntaisiin komponentteihin.
1.6 Pistetulo
Vektorien pistetulo (eli skalaaritulo)
Vektorien \(\bar{a}=a_{x}\bar{i}+a_{y}\bar{j}+a_{z}\bar{k}\) ja \(\bar{b}=b_{x}\bar{i}+b_{y}\bar{j}+b_{z}\bar{k}\) pistetulo lasketaan
$$\bar{a}\cdot \bar{b}=a_{x}b_{x}+a_{y}b_{y}+a_{z}b_{z}.$$
Esim. 1
Laske vektorien \(\bar{a}=2\bar{i}-\bar{j}+3\bar{k}\) ja \(\bar{b}=-3\bar{i}+5\bar{j}+4\bar{k}\) pistetulo.
Vastaus: \(1\).
Vektorien kohtisuoruusehto
Vektorit \(\bar{a}\) ja \(\bar{b}\), jotka eivät ole nollavektoreita, ovat kohtisuorassa toisiaan vastaan, jos ja vain jos niiden pistetulo \(\bar{a}\cdot \bar{b}\) on nolla eli
$$\bar{a}\perp \bar{b}\quad \Leftrightarrow \quad \bar{a}\cdot \bar{b}=0 \quad (\bar{a}\neq\bar{0}, \bar{b}\neq\bar{0}).$$
Esim. 2
Tutki, ovatko vektorit \(\bar{a}=2\bar{i}-3\bar{j}+\bar{k}\) ja \(\bar{b}=5\bar{i}+4\bar{j}+2\bar{k}\) kohtisuorassa toisiaan vastaan.
Vastaus: Kyllä, koska pistetulo on nolla.
Vektorien pistetulon ominaisuuksia
(1) Pistetulon vaihdannaisuus
$$\bar{a}\cdot \bar{b}=\bar{b}\cdot \bar{a}$$
(2) Osittelu
$$\bar{a}\cdot(\bar{b}+\bar{c})=\bar{a}\cdot \bar{b}+\bar{a}\cdot \bar{c}$$
(3) Kertoimen siirtosääntö
$$(s\bar{a})\cdot (t\bar{b})=(st)\bar{a}\cdot \bar{b}$$
(4) Vektorin pistetulo itsensä kanssa
$$\bar{a}\cdot \bar{a}=\left|\bar{a}\right|^{2}$$
1.7 Vektorien välinen kulma
Vektorien välisen kulman laskeminen
Olkoon vektorit \(\bar{a}\) ja \(\bar{b}\), jotka eivät ole nollavektoreita. Tällöin vektorien \(\bar{a}\) ja \(\bar{b}\) välinen kulma voidaan ratkaista yhtälöstä
$$\cos \left(\bar{a}, \bar{b}\right)=\frac{\bar{a}\cdot \bar{b}}{\left|\bar{a}\right|\left|\bar{b}\right|},$$ missä \(\cos \left(\bar{a}, \bar{b}\right)=\cos \left(\sphericalangle \left(\bar{a}, \bar{b}\right)\right)\).
Esim. 1
Laske vektorien \(\bar{a}=4\bar{i}-2\bar{j}+7\bar{k}\) ja \(\bar{b}=6\bar{i}+3\bar{j}-5\bar{k}\) välinen kulma.
Vastaus: \(\sphericalangle \left(\bar{a}, \bar{b}\right)\approx{104^\circ}\).
1.8 Determinantti
Kolmirivinen determinantti:
\(\left|\begin{array}{ccc} \bar{i} &\bar{j}&\bar{k}\\ a_{x}&a_{y}&a_{z}\\ b_{x}&b_{y}&b_{z} \end{array}\right|\)
Alkion \(\bar{i}\) kaksirivinen alideterminantti:
\(\left|\begin{array}{cc} a_{y}&a_{z}\\ b_{y}&b_{z} \end{array}\right|\)
Alkion \(\bar{j}\) kaksirivinen alideterminantti:
\(\left|\begin{array}{cc} a_{x}&a_{z}\\ b_{x}&b_{z} \end{array}\right|\)
Alkion \(\bar{k}\) kaksirivinen alideterminantti:
\(\left|\begin{array}{cc} a_{x}&a_{y}\\ b_{x}&b_{y} \end{array}\right|\)
Alkion \(\bar{i}\) kaksirivisen alideterminantin laskeminen:
\(\left|\begin{array}{cc} a_{y}&a_{z}\\ b_{y}&b_{z} \end{array}\right|=a_{y}b_{z}-a_{z}b_{y}\)
Alkioiden \(\bar{j}\) ja \(\bar{k}\) kaksiriviset alideterminantit lasketaan vastaavasti.
1.9 Ristitulo
Vektoreiden \(\bar{a}\) ja \(\bar{b}\) ristitulo (eli vektoritulo)
- merkitään \(\bar{a}\times\bar{b}\)
- tuottaa tuloksena vektorin, joka on kohtisuorassa vektoreiden \(\bar{a}\) ja \(\bar{b}\) tasoa vastaan
- lasketaan determinantin avulla seuraavasti.
Esim. 1
Laske vektorien \(\bar{a}=4\bar{i}-2\bar{j}+7\bar{k}\) ja \(\bar{b}=6\bar{i}+3\bar{j}-5\bar{k}\) ristitulo.
\(\begin{align} \bar{a}\times\bar{b}&=\left|\begin{array}{ccc} \bar{i} &\bar{j}&\bar{k}\\ 4&-2&7\\ 6&3&-5 \end{array}\right|\\ &\\ &=\left|\begin{array}{cc} -2&7\\ 3&-5 \end{array}\right|\bar{i}-\left|\begin{array}{cc} 4&7\\ 6&-5 \end{array}\right|\bar{j}+\left|\begin{array}{cc} 4&-2\\ 6&3 \end{array}\right|\bar{k}\\ &\\ &=(-2\cdot(-5)-7\cdot3)\bar{i}-(4\cdot(-5)-7\cdot6)\bar{j}+(4\cdot3-(-2)\cdot6)\bar{k}\\ &\\ &=(10-21)\bar{i}-(-20-42)\bar{j}+(12-(-12))\bar{k}\\ &\\ &=-11\bar{i}+62\bar{j}+24\bar{k} \end{align}\)
Vastaus: \(\bar{a}\times\bar{b}=-11\bar{i}+62\bar{j}+24\bar{k}\)
Huom.
Vektorien ristitulo lasketaan GeoGebralla komennolla Ristitulo(vektori, vektori).
Vektorien ristitulon ominaisuuksia
(1) Ristitulo ei ole vaihdannainen
\(\bar{b}\times\bar{a}=-\bar{a}\times\bar{b}\)
(2) Osittelu
\(\bar{a}\times(\bar{b}+\bar{c})=\bar{a}\times\bar{b}+\bar{a}\times\bar{c}\)
\((\bar{a}+\bar{b})\times\bar{c}=\bar{a}\times\bar{c}+\bar{b}\times\bar{c}\)
(3) Kertoimen siirtosääntö
\((t\bar{a})\times\bar{b}=t(\bar{a}\times\bar{b})\)
\(\bar{a}\times(t\bar{b})=t(\bar{a}\times\bar{b})\)
Vektorien yhdensuuntaisuus
Olkoon \(\bar{a}\) ja \(\bar{b}\) kaksi xyz-koordinaatiston vektoria, jotka eivät ole nollavektoreita. Vektorit \(\bar{a}\) ja \(\bar{b}\) ovat yhdensuuntaiset täsmälleen silloin, kun niiden ristitulo on nollavektori eli
$$\bar{a}\parallel\bar{b}\quad\Leftrightarrow\quad\bar{a}\times\bar{b}=\bar{0}\quad(\bar{a}\neq\bar{0},\bar{b}\neq\bar{0}).$$
1.10 Suunnikkaan pinta-ala
Suunnikkaan, jonka sivuina ovat vektorit \(\bar{a}\) ja \(\bar{b}\), pinta-ala on vektoreiden \(\bar{a}\) ja \(\bar{b}\) ristitulona saatavan vektorin pituus.
Suunnikkaan pinta-ala
$$A_{SUUNNIKAS}=\left|\bar{a}\times\bar{b}\right|=\left|\bar{a}\right|\left|\bar{b}\right|\sin(\bar{a},\bar{b})$$
Esim. 1
Suunnikkaan kärkipisteet ovat \(A=(1,-1,3)\), \(B=(2,1,1)\), \(C=(3,2,4)\) ja \(D\). Laske suunnikkan \(ABCD\) pinta-ala.
1.11 Skalaarikolmitulo
Merkintä
Vektorien \(\bar{a}\), \(\bar{b}\) ja \(\bar{c}\) skalaarikolmitulo merkitään $$(\bar{a}\times\bar{b})\cdot\bar{c}.$$
Skalaarikolmitulo \((\bar{a}\times\bar{b})\cdot\bar{c}\) voidaan suorittaa laskemalla ensin ristitulo \(\bar{a}\times\bar{b}\) ja sitten pistetulo saadun vektorin ja vektorin \(\bar{c}\) kesken.
Suuntaissärmiön tilavuus
Vektorien \(\bar{a}\), \(\bar{b}\) ja \(\bar{c}\) määräämän suuntaissärmiön tilavuus on $$V=\left|(\bar{a}\times\bar{b})\cdot\bar{c}\right|.$$
Esim. 1
Laske vektorien \(\bar{a}=3\bar{i}+\bar{j}-2\bar{k}\), \(\bar{b}=2\bar{i}-2\bar{j}+\bar{k}\) ja\(\bar{c}=-\bar{i}+3\bar{j}-\bar{k}\) määräämän suuntaissärmiön tilavuus.
2 AVARUUSGEOMETRIA
2.1 Suoran suuntavektori
Avaruuden suoran määrää yksikäsitteisesti jompikumpi:
1) kaksi pistettä
2) piste ja suuntavektori.
Suoran suuntavektori
Suoran suuntavektori on suoran kanssa yhdensuuntainen vektori \(\bar{v}\).
Esim. 1
Suora kulkee xyz-koordinaatistossa pisteen \(A\) kautta. Piste \(P\) on samalla suoralla. Suoran eräs suuntavektori on vektori \(\bar{v}\). Piirrä tilanteesta kuva ja määritä pisteelle \(P\) lauseke.
2.2 Suoran vektoriyhtälö
Suoran vektoriyhtälö
Olkoon \(A\) yksi suoran piste ja \(\bar{v}\) suoran suuntavektori sekä \(t\) reaaliluku. Tällöin minkä tahansa suoran pisteen \(P\) paikkavektori voidaan esittää muodossa $$\overline{OP}=\overline{OA}+t\bar{v}.$$
Yhtälö on suoran vektoriyhtälö
Esim. 1
Suora kulkee pisteen \(A=(2,-1,3)\) kautta ja sen suuntavektori on \(\bar{v}=3\bar{i}-4\bar{j}-\bar{k}\). Määritä suoran vektoriyhtälö ja pisteen \(A\) lisäksi toinen suoran piste.
2.3 Suoran parametriesitys
Olkoon \(A=(x_0,y_0,z_0)\) yksi suoran piste ja \(\bar{v}=v_{x}\bar{i}+v_{y}\bar{j}+v_{z}\bar{k}\) suoran suuntavektori.
Tällöin suoran vektoriyhtälö eli suoran pisteen \(P\) paikkavektori on
$$ \begin{align} \overline{OP}&=\overline{OA}+t\bar{v}\\ &=x_{0}\bar{i}+y_{0}\bar{j}+z_{0}\bar{j}+t(v_{x}\bar{i}+v_{y}\bar{j}+v_{z}\bar{k})\\ &=x_{0}\bar{i}+y_{0}\bar{j}+z_{0}\bar{j}+tv_{x}\bar{i}+tv_{y}\bar{j}+tv_{z}\bar{k}\\ &=x_{0}\bar{i}+tv_{x}\bar{i}+y_{0}\bar{j}+tv_{y}\bar{j}+z_{0}\bar{j}+tv_{z}\bar{k}\\ &=(x_{0}+tv_{x})\bar{i}+(y_{0}+tv_{y})\bar{j}+(z_{0}+tv_{z})\bar{k} \end{align} $$
Suoran vektoriyhtälön eli pisteen \(P\) paikkavektorin komponenttien kertoimet ovat pisteen \(P\) koordinaatit. Koska piste \(P\) on suoran mielivaltainen piste, olemme saaneet esityksen suoran pisteille.
Suoran parametriesitys
Olkoon \((x_0,y_0,z_0)\) yksi suoran piste ja \(\bar{v}=v_{x}\bar{i}+v_{y}\bar{j}+v_{z}\bar{k}\) suoran suuntavektori sekä \(t\) reaaliluku. Tällöin suoran pisteiden koordinaatit \((x,y,z)\) voidaan esittä muodossa
\(\begin{cases}x=x_{0}+tv_{x}\\y=y_{0}+tv_{y}\\z=z_{0}+tv_{z}\end{cases}\)
Yhtälöryhmä on suoran parametriesitys.
Esim. 1
Suora kulkee pisteen \(A=(2,-1,3)\) kautta ja sen suuntavektori on \(\bar{v}=3\bar{i}-4\bar{j}-\bar{k}\)
a) Määritä suoran parametriesitys.
b) Onko piste \(B=(-4,7,5)\) suoralla?
c) Missä pisteessä suora leikkaa xy-tason?
2.4 Suorat leikkaavat avaruudessa
Esim. 1
Suora \(l\) kulkee pisteiden \(A=(-1,2,0)\) ja \(B=(7,0,10)\) kautta ja suora \(m\) pisteiden \(C=(4,-1,2)\) ja \(D=(2,3,8)\) kautta. Määritä suorien \(l\) ja \(m\) leikkauspiste ja välinen kulma
a) GeoGebralla piirtämällä
b) laskemalla.
a) GeoGebra.
b) Leikkauspiste:
Määritetään suorien \(l\) ja \(m\) suuntavektorit.
\(\begin{align} l:\quad\overline{AB}&=(7-(-1))\bar{i}+(0-2)\bar{j}+(10-0)\bar{k}\\ &=8\bar{i}-2\bar{j}+10\bar{k} \end{align}\)
\(\begin{align} m:\quad\overline{CD}&=(2-4))\bar{i}+(3-(-1))\bar{j}+(8-2)\bar{k}\\ &=-2\bar{i}+4\bar{j}+6\bar{k} \end{align}\)
Määritetään suorien parametriesitykset.
\(l:\quad\begin{cases} x&=-1+t\cdot8&=8t-1\\ y&=2+t\cdot(-2)&=-2t+2\\ z&=0+t\cdot10&=10t \end{cases}\)
\(m:\quad\begin{cases} x&=4+t\cdot(-2)&=-2t+4\\ y&=-1+t\cdot4&=4t-1\\ z&=2+t\cdot6&=6t+2 \end{cases}\)
Suorien leikkauspiste on suorien yhteinen piste. Muodostetaan yhtälöryhmä.
TAPA 1: (ilman laskinta)
\(\begin{cases} 8t-1&=-2t+4\\ -2t+2&=4t-1\\ 10t&=6t+2 \end{cases}\)
\(\Leftrightarrow\begin{cases} 10t&=5\\ -6t&=-3\\ 4t&=2 \end{cases}\)
\(\Leftrightarrow\begin{cases} t&=\frac{1}{2}\\ t&=\frac{1}{2}\\ t&=\frac{1}{2} \end{cases}\)
\(\Rightarrow\begin{cases} x&=8\cdot\frac{1}{2}-1=4-1=3\\ y&=-2\cdot\frac{1}{2}+2=-1+2=1\\ z&=10\cdot\frac{1}{2}=5 \end{cases}\)
TAPA 2: (laskimella)
\(\begin{cases} x&=8t-1\\ y&=-2t+2\\ z&=10t\\ x&=-2t+4\\ y&=4t-1 \end{cases}\)
GeoGebran Ratkaise-toiminto tai -komento:
\(x=3\), \(y=1\), \(z=5\), \(t=\frac{1}{2}\).
Suorien välinen kulma:
Määritetään suuntavektoreiden \(\overline{AB}\) ja \(\overline{CD}\) välinen kulma.
\(\begin{align} \left|\overline{AB}\right|&=\sqrt{8^2+(-2)^2+10^2}\\ &=\sqrt{64+4+100}\\ &=\sqrt{168}\\ &=2\sqrt{42} \end{align}\)
\(\begin{align} \left|\overline{CD}\right|&=\sqrt{(-2)^2+4^2+6^2}\\ &=\sqrt{4+16+36}\\ &=\sqrt{56}\\ &=2\sqrt{14} \end{align}\)
\(\begin{align} \overline{AB}\cdot\overline{CD}&=8\cdot(-2)+(-2)\cdot4+10\cdot6\\ &=-16-8+60\\ &=-24+60\\ &=36 \end{align}\)
\(\begin{align} \cos\left(\overline{AB},\overline{CD}\right)&=\frac{\overline{AB}\cdot\overline{CD}}{\left|\overline{AB}\right|\left|\overline{CD}\right|}\\ \cos\left(\overline{AB},\overline{CD}\right)&=\frac{\overline{AB}\cdot\overline{CD}}{2\sqrt{42}\cdot2\sqrt{14}}\\ \sphericalangle\left(\overline{AB},\overline{CD}\right)&=68{,}2132\ldots^{\circ}\\ &\approx68{,}2^{\circ} \end{align}\)
Vastaus: Leikkauspiste on \((3,1,5)\) ja suorien välinen kulma \(68{,}2^{\circ}\).
2.5 Taso avaruudessa
Tason määrää yksikäsitteisesti jokin seuraavista:
1) kolme pistettä
2) piste ja kaksi samassa tasossa olevaa vektoria
3) yksi piste ja tason normaalivektori eli tasoa vastaan kohtisuora vektori.
Tason koordinaattiyhtälö
Olkoon \((x_0,y_0,z_0)\) yksi tason piste ja \(\bar{n}=a\bar{i}+b\bar{j}+c\bar{k}\) tason eräs normaalivektori.
Tällöin tason pisteet \((x,y,z)\) toteuttavat tason koordinaattiyhtälön:
$$a(x-x_0)+b(y-y_0)+c(z-z_0)=0.$$
Huom.
Tason koordinaattiyhtälö voidaan aina sieventää tason yhtälön normaalimuotoon.
Tason yhtälön normaalimuoto
$$ax+by+cz+d=0,$$
missä \(d\) on reaaliluku.
Esim. 1
Pisteet \(A=(-1,3,-2)\), \(B=(4,2,5)\) ja \(C=(2,5,1)\) määräävät tason.
a) Määritä piirtämällä GeoGebralla tason yhtälön normaalimuoto.
b) Määritä laskemalla tason koordinaattiyhtälö.
c) Määritä laskemalla tason yhtälön normaalimuoto.
a) GeoGebralla:
\(-17x+6y+13z=9\)
\(\Leftrightarrow-17x+6y+13z-9=0\).
Vastaus: \(-17x+6y+13z-9=0\)
b) Tulossa.
c) Tulossa.
2.6 Suora leikkaa tasoa
Esim. 1
Määritä laskemalla, missä pisteessä suora \(\begin{cases}x=2-t\\y=-1+2t\\z=-t\end{cases}\) leikkaa tason \(2x-3y+z+2=0\).
Tulossa.
Vastaus: \((1,1,-1)\).
Huom.
Suora voi myös kulkea tasossa (ääretön määrä yhteisiä pisteitä) tai tason suuntaisesti tason ulkopuolella (ei yhteisiä pisteitä).
Suoran ja tason välinen kulma
Suoran \(l\) ja tason \(T\) välinen kulma tarkoittaa suoran \(l\) ja sen kohtisuoran projektion \(p\) tasolle \(T\) välistä kulmaa \(\alpha\).
Kulma \(\alpha\) on aina välillä \(0^{\circ}\lt\alpha\lt90^{\circ}\).
Kulma \(\alpha\) voidaan laskea suoran suuntavektorin \(\bar{s}\) ja tason normaalivektorin \(\bar{n}\) välisen kulman \(\beta\) avulla.
Jos \(0^{\circ}\lt\beta\lt90^{\circ}\) (terävä kulma), niin \(\alpha=90^{\circ}-\beta\).
Jos \(90^{\circ}\lt\beta\lt180^{\circ}\) (tylppä kulma), niin \(\alpha=\beta-90^{\circ}\).
Esim. 2
Määritä laskemalla suoran \(\begin{cases}x=2-t\\y=-1+2t\\z=-t\end{cases}\) ja tason \(2x-3y+z+2=0\) välinen kulma.
Tulossa.
Vastaus: \(79{,}1^{\circ}\).
2.7 Taso leikkaa tasoa
Tasojen välinen kulma \(\alpha\) voidaa määrittää laskemalla tasojen normaalivektoreiden välinen kulma.
Esim. 1
Määritä laskemalla tason \(2x-3y+z+2=0\) ja xy-tason välinen kulma.
Tason \(2x-3y+z+2=0\) eräs normaalivektori on \(\bar{n}=2\bar{i}-3\bar{j}+\bar{k}\) ja xy-tason eräs normaalivektori \(\bar{m}=\bar{k}\).
Lasketaan normaalivektorien välinen kulma.
\(\left|\bar{n}\right|=\sqrt{2^2+(-3)^2+1^2}=\sqrt{14}\)
\(\left|\bar{m}\right|=1\)
\(\bar{n}\cdot\bar{m}=2\cdot0+(-3)\cdot0+1\cdot1=1\)
\(\begin{align} \cos\left(\bar{n},\bar{m}\right)&=\frac{\bar{n}\cdot\bar{m}}{\left|\bar{n}\right|\left|\bar{m}\right|}\\ \cos\left(\bar{n},\bar{m}\right)&=\frac{1}{\sqrt{14}\cdot1}\quad\mid\arccos\\ \sphericalangle\left(\bar{n},\bar{m}\right)&=74{,}498\ldots^{\circ}\approx74{,}5^{\circ} \end{align}\)
Vastaus: Tasojen välinen kulma on \(74{,}5^{\circ}\).
2.8 Pisteen etäisyys suorasta
Esim. 1
Suora kulkee pisteiden \(A=(3,1,4)\) ja \(B=(2,-1,5)\) kautta. Määritä ensin GeoGebralla sitten laskemalla
a) suoran piste, joka on lähimpänä pistettä \(P=(5,-6,4)\)
b) pisteen \(P\) etäisyys suorasta.
Tulossa.
Vastaus: \((1,-3,6)\) ja \(\sqrt{29}\).
2.9 Pisteen etäisyys tasosta
Esim. 1
Tason määräävät pisteet \(A=(1,1,7)\), \(B=(0,0,2)\) ja \(C=(-1,-1,3)\). Määritä ensin GeoGebralla sitten laskemalla
a) tason piste, joka on lähimpänä pistettä \(P=(1,-5,3)\)
b) pisteen \(P\) etäisyys tasosta.
Tulossa.
Vastaus: \((3,-2,2)\).
Pisteen etäisyys tasosta
Pisteen \(P=(x_0,y_0,z_0)\) etäisyys \(\delta\) tasosta \(ax+by+cz+d=0\) voidaan laskea kaavalla $$\delta=\frac{\left|ax_0+by_0+cz_0+d\right|}{\sqrt{a^2+b^2+c^2}}.$$
2.10 Avaruuskappaleita
Esim. 1
Suorakulmaisen särmiön leveys on 3, syvyys 2 ja korkeus 1. Määritä suorakulmaisen särmiön pohjan lävistäjän ja avaruuslävistäjän välinen kulma.
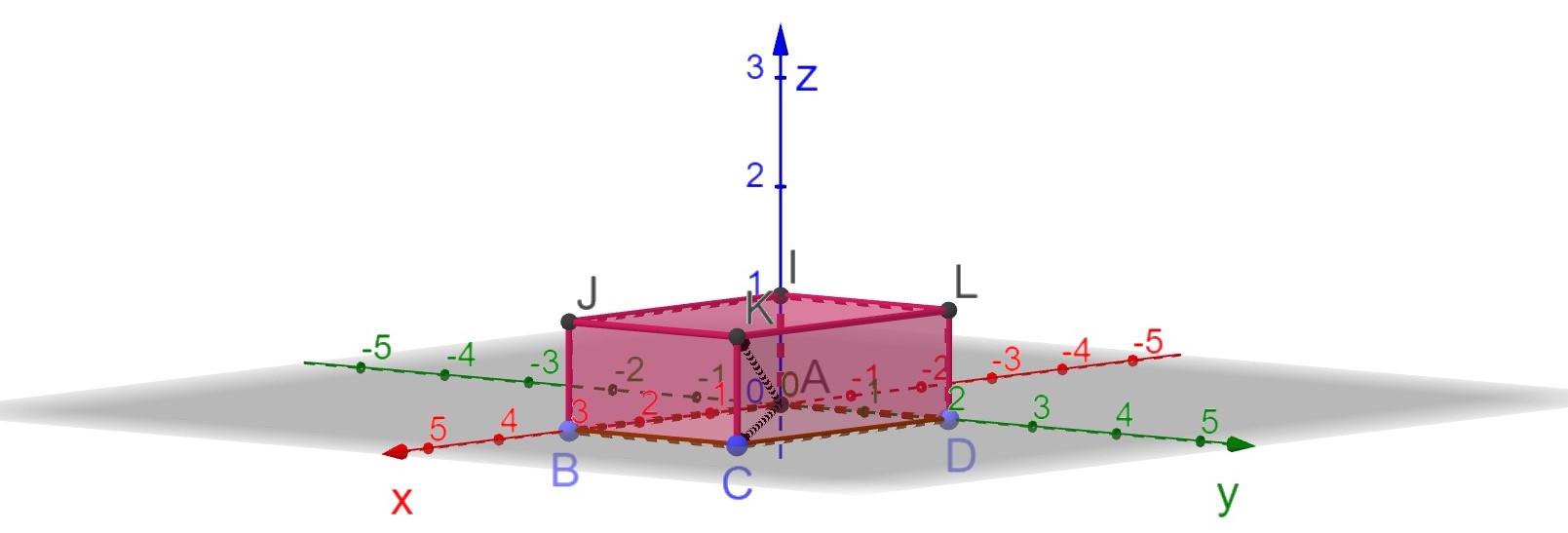
TAPA 1:
Pohjan lävistäjä vastaa kuvassa vektoria \(\overline{AC}=3\bar{i}+2\bar{j}\) ja avaruuslävistäjä vektoria \(\overline{AK}=3\bar{i}+2\bar{j}+\bar{k}\).
Ratkaistaan vektorien välinen kulma kaavasta:
\(\cos\left(\bar{a},\bar{b}\right)=\displaystyle{\frac{\bar{a}\cdot\bar{b}}{\left|\bar{a}\right|\left|\bar{b}\right|}}\).
\(\left|\overline{AC}\right|=\sqrt{3^2+2^2}=\sqrt{13}\)
\(\left|\overline{AK}\right|=\sqrt{3^2+2^2+1^2}=\sqrt{14}\)
\(\overline{AC}\cdot\overline{AK}=3\cdot3+2\cdot2+0\cdot1=13\)
\(\begin{align} \cos\left(\overline{AC},\overline{AK}\right)&=\frac{13}{\sqrt{13}\cdot\sqrt{14}}\quad\mid\arccos\\ \sphericalangle\left(\overline{AC},\overline{AK}\right)&=15{,}501\ldots^{\circ}\\&\approx15{,}5^{\circ} \end{align}\)
TAPA 2:
Kosinilause.
Vastaus: \(15{,}5^{\circ}\).
2.11 Ääriarvosovelluksia
Esim. 1
Neliöpohjaisen suoran pyramidin korkeuden ja pohjan särmän pituuksien summa on 12. Määritä pyramidin suurin mahdollinen tilavuus.
Korkeuden ja pohjan särmän pituuksien summa on 12:
\(a+h=12 \quad \Leftrightarrow \quad h=12-a\).
Pyramidin tilavuus on:
\(\begin{aligned}[r&l&l] V&=\frac{1}{3}A_{pohja}h &\mid A_{pohja}=a^2\\ &=\frac{1}{3}a^{2}h &\mid h=12-a\ \\ &=\frac{1}{3}a^2(12-a)\\ &=4a^2-\frac{1}{3}a^3 \end{aligned}\)
Merkitään tilavuusfunktio \(V(a)=4a^2-\frac{1}{3}a^3\).
Derivoidaan.
\(\begin{aligned}[r&l] V'(a)&=4\cdot2a-\frac{1}{3}\cdot3a^2\\ &=8a-a^2 \end{aligned}\)
Derivaattafunktion nollakohdat:
\(\begin{aligned}[r&l] V'(a)&=0\\ 8a-a^2&=0\\ a(8-a)&=0\\ a=0 \quad &\text{tai} \quad 8-a=0\\ &\quad \quad \quad \quad a=8 \end{aligned}\)
Testipisteet:
\(V'(-1)=8\cdot(-1)-(-1)^2=-8-1=-9\lt0\)
\(V'(1)=8\cdot1-1^2=8-1=7\gt0\)
\(V'(10)=8\cdot10-10^2=80-100=-20\lt0\)
Kulkukaavio:
\(\begin{matrix} &0&&8&\\ \hline \ \ \ -&\mid&+&\mid&-\ \ \ \\ \hline \ \ \ \searrow&\mid&\nearrow&\mid&\searrow\ \ \ \\ \hline \end{matrix}\)
Funktio \(V\) saa pienimmän arvonsa, kun \(a=0\), ja suurimman, kun \(a=8\).
Pyramidin suurin mahdollinen tilavuus on:
\(\begin{aligned}[r&l&l] V(8)&=\frac{1}{3}\cdot8^2(12-8)\\ &=\frac{1}{3}\cdot64\cdot4\\ &=\frac{256}{3} \end{aligned}\)
Vastaus: \(\frac{256}{3}\).
Esim. 2
Suoran ympyräkartion sisään on sijoitettu suurin mahdollinen suora ympyrälieriö, jonka pohjan halkaisija ja korkeus ovat \(d\). Määritä kuvaukseen sopivan pienimmän mahdollisen ympyräkartion mitat.
3 KAHDEN MUUTTUJAN FUNKTIO
3.1 Kahden muuttujan funktio
Funktiossa voi olla useampia kuin yksi muuttuja. Jos muuttujia on kaksi, on kyseessä kahden muuttujan funktio.
Esim. 1
Laske funktion \(f(x,y)=x^2+y^2-4x-2y-4\) arvo kohdassa \((2,-1)\).
\(\begin{align} f(2,-1)&=2^2+(-1)^2-4\cdot2-2\cdot(-1)-4\\ &=4+1-8+2-4\\ &=-5 \end{align}\)
Vastaus: \(f(2,-1)=-5\)
Funktion kuvaaja \(z=f(x,y)\) on pinta, joka muodostuu pisteistä \(\left(x,y,z\right)=\left(x,y,f(x,y)\right)\).
Esim. 2
Piirrä funktion \(f(x,y)=x^2+y^2-4x-2y-4\) kuvaaja GeoGebralla.
Nollakohdat
Kahden muuttujan funktion nollakohdat ovat kaikki kohdat \((x,y)\), joilla \(f(x,y)=0\). Nollakohdissa kuvaajan pisteen z-koordinaatti on nolla. Nollakohdat ovat graafisesti tulkittuna kuvaajan ja xy-tason leikkauskohtia.
Esim. 3
Määritä funktion \(f(x,y)=x^2+y^2-4x-2y-4\) nollakohdat ja piirrä GeoGebralla nollakohtien joukko funktion kuvaajalle.
Merkitään
\(\begin{align} f(x,y)&=0\\ x^2+y^2-4x-2y-4&=0 \end{align}\)
Muokataan yhtälö muotoon, jossa nollakohtien joukko voidaan tunnistaa. Koska yhtälö muistuttaa ympyrän yhtälöä, yritetään muokata se ympyrän yhtälöksi neliöihin täydentämällä.
\(\begin{eqnarray} x^2-4x+y^2-2y&=&4 &\mid& +~4\ +1\quad\quad\quad\quad\quad\quad\quad\\ x^2-4x+4+y^2-2y+1&=&4+4+1\quad &\mid& a^2-2ab+b^2=(a-b)^2\\ (x-2)^2+(y-1)^2&=&9&& \end{eqnarray}\)
Nollakohtien joukko on xy-tason ympyrä, jonka keskipiste on \((2,1)\) ja säde \(\sqrt{9}=3\).
Määrittelyjoukko
Funktion \(f(x,y)\) määrittelyjoukko on xy-taso tai sen osajoukko.
Esim. 4
Mikä on funktion \(f(x,y)=\sqrt{x^2-y-4}\) määrittelyehto?
Neliöjuuri on määritelty, kun juurrettava on epänegatiivinen.
\(\begin{align} x^2-y-4&\ge0\\ x^2-4&\ge y \end{align}\)
Vastaus: määrittelyehto: \(y\le x^2-4\).
3.2 Osittaisderivaatta
Kahden muuttujan funktion \(f(x,y)\) osittaisderivaattafunktio muuttujan \(x\) suhteen saadaan derivoimalla funktiota \(f\) muuttujana \(x\) ja pitämällä \(y\) vakiona. Merkitään \(\partial_{x}f(x,y)\) tai \(D_{x}f(x,y)\) tai \(f_{x}(x,y)\).
Kahden muuttujan funktion \(f(x,y)\) osittaisderivaattafunktio muuttujan \(y\) suhteen saadaan derivoimalla funktiota \(f\) muuttujana \(y\) ja pitämällä \(x\) vakiona. Merkitään \(\partial_{y}f(x,y)\) tai \(D_{y}f(x,y)\) tai \(f_{y}(x,y)\).
Funktion \(f\) osittaisderivaatta on funktion \(f\) osittaisderivaattafunktion arvo tietyssä xy-tason kohdassa.
Esim. 1
Määritä funktion \(f(x,y)=\frac{1}{2}x^2+xy^2-2x+3y\)
a) osittaisderivaattafunktiot
b) osittaisderivaatat kohdassa \((-1,1)\).
a) Määritetään osittaisderivaattafunktiot.
\(\begin{align}\partial_{x}f(x,y)&=\frac{1}{2}\cdot2x+y^2-2\\&=x+y^2-2\end{align}\)
\(\begin{align}\partial_{y}f(x,y)&=x\cdot2y+3\\&=2xy+3\end{align}\)
Vastaus: \(\partial_{x}f(x,y)=x+y^2-2\) ja \(\partial_{y}f(x,y)=2xy+3\).
b) Määritetään osittaisderivaatat kohdassa \((-1,1)\).
\(\begin{align}\partial_{x}f(-1,1)&=-1+1^2-2\\&=-2\end{align}\)
\(\begin{align}\partial_{y}f(-1,1)&=2\cdot(-1)\cdot1+3\\&=1\end{align}\)
Vastaus: \(\partial_{x}f(-1,1)=-2\) ja \(\partial_{y}f(-1,1)=1\)
Kriittinen piste
Kriittiset pisteet ovat kahden muuttujan funktion ääriarvokohtia tai niin sanottuja satulapisteitä (vrt. yhden muuttujan funktion terassikohta).
Kahden muuttujan funktion kriittiset pisteet määritetään osittaisderivaattojen nollakohtien avulla. Kriittisen pisteen koordinaatit saadaan ratkaisemalla yhtälöpari
\(\begin{cases}\partial_{x}f(x,y)=0\\ \partial_{y}f(x,y)\ \!=0\end{cases}\).
Esim. 2
Määritä funktion \(f(x,y)=x^3-y^2-3x+4y\)
a) kriittiset pisteet
b) kriittisten pisteiden laatu.
a) Määritetään osittaisderivaattafunktiot.
\(\partial_{x}f(x,y)=3x^2-3\)
\(\partial_{y}f(x,y)=-2y+4\)
Muodostetaan yhtälöpari ja ratkaistaan kriittiset pisteet.
\(\begin{cases} \partial_{x}f(x,y)=0\\ \partial_{y}f(x,y)=0 \end{cases}\)
\(\begin{cases} 3x^2-3=0\\ -2y+4=0 \end{cases} \quad\mid \text{CAS-laskin}\)
\(\begin{cases} x=1\\ y=2 \end{cases}\) tai \(\begin{cases} x=-1\\ y=2 \end{cases}\)
Vastaus: Kriittiset pisteet ovat \((1,2)\) tai \((-1,2)\).
b) Piirretään funktion kuvaaja GeoGebralla. Kuvasta nähdään, että kohta \((1,2)\) on satulapiste ja kohta \((-1,2)\) maksimikohta.
3.3 Tasa-arvokäyrät
Tasa-arvokäyrä on kaikkien niiden pisteiden joukko, jotka toteuttavat yhtälön \(f(x,y)=c\). Toisin sanoen se on kyseisen yhtälön ratkaisujoukko.
Esim. 1
Määritä funktion \(f(x,y)=\sqrt{x^2+y}\) tasa-arvokäyrä \(f(x,y)=2\) ja piirrä se GeoGebralla näkyviin funktion kuvaajalle.
Selvitetään funktion \(f(x,y)=\sqrt{x^2+y}\) määrittelyehto.
\(\begin{align}x^2+y&\ge0\\ y&\ge-x^2\end{align}\)
Määritetään tasa-arvokäyrä \(f(x,y)=2\).
\(\begin{align} \sqrt{x^2+y}&=2\quad\mid\ ()^{2}\\ x^2+y&=4\\ y&=-x^2+4 \end{align}\)
Tasa-arvokäyrä on xy-tason alaspäin (y-akselin negatiiviseen suuntaan) aukeava paraabeli \(y=-x^2+4\).
Piirretään lopuksi kuva GeoGebralla.
Huom.
Kartan korkeuskäyrät ovat käytännössä tasa-arvokäyriä.