Algoritmit ja lukuteoria (MAA11)
Laajuus
2 op
Yleiset tavoitteet (LOPS 2021)
Moduulin tavoitteena on, että opiskelija
- tietää, mikä on algoritmi, sekä oppii tutkimaan, kuinka algoritmit toimivat
- oppii toteuttamaan yksinkertaisia algoritmeja ohjelmoimalla
- perehtyy logiikan käsitteisiin
- hallitsee lukuteorian peruskäsitteet ja perehtyy alkulukujen ominaisuuksiin
- osaa tutkia kokonaislukujen jaollisuutta.
Keskeiset sisällöt (LOPS 2021)
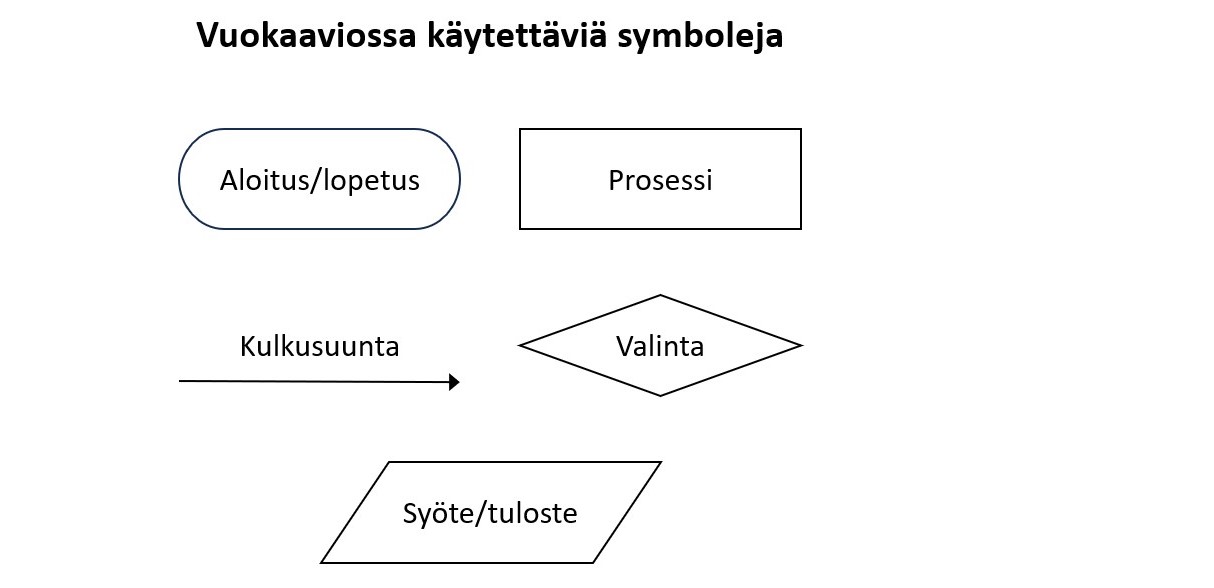
- algoritmisen ajattelun peruskäsitteet: peräkkäisyys, valinta ja toisto
- vuokaavio
- yksinkertaisten algoritmien, lajittelualgoritmien tai yhtälön numeeriseen ratkaisuun liittyvän algoritmin ohjelmointi
- konnektiivit ja totuusarvot
- kokonaislukujen jaollisuus, jakoyhtälö ja kongruenssi
- Eukleideen algoritmi
- aritmetiikan peruslause
Aikataulu
Suoritus
- osallistuminen
- tehtävien tekeminen
- monivalintatehtävien tekeminen
- loppukoe
Arviointi
- säännöllinen, aktiivinen ja vastuullinen osallistuminen +1 p
- tehtävien asianmukainen ja jatkuva tekeminen +1 p
- monivalintatehtävistä +1 p kustakin tehdystä monivalintakokonaisuudesta, saavutettava tavoitetaso 80 %, yht. max. 4 p
- loppukokeesta max. 56 p
- max. 60 p (teoreettisesti 62 p)
- 30 % arviointi
| Pisteet | Arvosana | Muuta |
|---|---|---|
| 0 - 9 | i \(\rightarrow\) K | Pakko täydentää. |
| 10 - 17 | i \(\rightarrow\) 4 | Oikeus täydentää. |
| 18 - 25 | 5 | |
| 26 - 33 | 6 | |
| 34 - 41 | 7 | |
| 42 - 49 | 8 | |
| 50 - 57 | 9 | |
| 58 - 60 | 10 |
Keskeyttäminen
Opettaja keskeyttää opiskelijan opintojakson, jos
- opiskelija niin pyytää
- opiskelija ei ole läsnä opintojakson kahdella ensimmäisellä opetuskerralla ja opiskelija ei ole yhteydessä opettajaan eikä opettaja saa yhteyttä opiskelijaan.
Opettaja voi keskeyttää opiskelijan opintojakson, jos opiskelijalla on viisi poissaoloa. Tällaiset tilanteet opettaja käy läpi tapauskohtaisesti ja on ennen lopullista keskeytystä yhteydessä opiskelijaan.
Keskeyttämisestä opettaja merkitsee opintojaksosta opiskelijalle K-merkinnän Wilmaan ja poistaa opiskelijan sen jälkeen Wilman ryhmästä. Opettaja lähettää keskeyttämisestä viestin opiskelijalle, alaikäisen opiskelijan huoltajalle, ryhmänohjaajalle ja opolle.
1 LOGIIKKA
1.1 Peruskäsitteitä
Logiikka on tieteenala, jonka kiinnostuksen kohteena on päättely. Matemaattisessa logiikassa luonnollisen kielen lauseet käännetään formaalille kielelle.
Atomilauseita merkitään isoilla kirjaimilla. Konnektiivien avulla atomilauseista voidaan muodostaa yhdistettyjä lauseita.
Merkitseminen konnektiivien avulla
| Merkintä | Nimitys | Lukutapa |
|---|---|---|
| \(\neg A\) | \(A\):n negaatio | ei \(A\) |
| \(A\wedge B\) | \(A\):n ja \(B\):n konjunktio | \(A\) ja \(B\) |
| \(A\vee B\) | \(A\):n ja \(B\):n disjunktio | \(A\) tai \(B\) |
| \(A\Rightarrow B\) | \(A\):n ja \(B\):n implikaatio (seuraus) | jos \(A\), niin \(B\) |
| \(A\Leftrightarrow B\) | \(A\):n ja \(B\):n ekvivalenssi (yhtäpitävyys) | \(A\), jos ja vain jos \(B\) |
Huom.
Matematiikassa tai-sana (eli konnektiivi \(\vee\)) tulkitaan inklusiivisesti ''jompikumpi tai molemmat''.
Monimutkaisempia yhdistettyjä lauseita voidaan muodostaa käytämällä sulkeita ja sopimalla konnektiivien keskinäisestä järjestyksestä.
Konnektiivien suoritusjärjestys
1) Negaatiot \(\neg\)
2) Konjunktiot \(\wedge\) ja disjunktiot \(\vee\)
3) Implikaatiot \(\Rightarrow\)
4) Ekvivalenssit \(\Leftrightarrow\)
Esim. 1
Formalisoi seuraavat luonnollisen kielen lauseet.
a) Aurinko paistaa ja on kuuma.
b) Jos aurinko ei paista, niin ei ole kuuma.
c) Joko aurinko paistaa tai on kuuma (mutta ei molemmat).
Esim. 2
Olkoon \(A\): ''sataa'', \(B\): ''tuulee'' ja \(C\): ''on myrsky''.
Suomenna lause \(C\Leftrightarrow(A\wedge B)\).
1.2 Totuusarvo
Väitelausetta, joka on joko tosi tai epätosi, kutsutaan suljetuksi lauseeksi eli propositioksi.
Merkitään toden lauseen totuusarvoa 1 ja epätoden 0.
Totuustaulut
| Negaatio | |
|---|---|
| \(A\) | \(\neg A\) |
| 1 | 0 |
| 0 | 1 |
| Konjunktio | ||
|---|---|---|
| \(A\) | \(B\) | \(A\wedge B\) |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| Disjunktio | ||
|---|---|---|
| \(A\) | \(B\) | \(A\vee B\) |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| Implikaatio | ||
|---|---|---|
| \(A\) | \(B\) | \(A\Rightarrow B\) |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| Ekvivalenssi | ||
|---|---|---|
| \(A\) | \(B\) | \(A\Leftrightarrow B\) |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Esim. 1
Millä lauseiden \(A\) ja \(B\) totuusarvoilla lause \(\neg\left(A\vee B\right)\) on tosi?
Esim. 2
Formalisoi lause ''Jos on pilvistä, niin kala syö hyvin, tai ei ole pilvistä ja kala syö hyvin''. Milloin lause ei ole tosi?
1.3 Tautologia
Tautologia on lause, joka on aina tosi.
Esim. 1
Osoita, että niin kutsuttu modus ponens -päättely \(A\wedge\left(A\Rightarrow B\right)\Rightarrow B\) on tautologia.
Kontradiktio on lause, joka on aina epätosi.
Esim. 2
Tutki, onko lause ''Olen parhaimmillani täsmälleen silloin, kun en ole parhaimmillani.'' kontradiktio.
Loogisesti yhtäpitävillä eli loogisesti ekvivalenteilla lauseilla on sama totuusarvo.
Esim. 3
Ovatko lauseet ''Jos on pimeää, niin on yö.'' ja ''Jos ei ole yö, niin ei ole pimeää.'' loogisesti yhtäpitävät?
2 LUKUTEORIA
2.1 Kokonaislukujen jaollisuus
Jaollisuus
Kokonaisluku \(a\) on jaollinen positiivisella kokonaisluvulla \(b\), jos on olemassa kokonaisluku \(q\), jolla pätee \(a=bq\).
Merkintä:
Luku \(12\) on jaollinen luvulla \(4\) voidaan merkitä: \(4\mid12\).
Luku \(15\) ei ole jaollinen luvulla \(4\) voidaan merkitä: \(4\cancel\mid15\).
Esim. 1
Osoita, että
a) luku 63 on jaollinen luvulla 7
b) luku 54 ei ole jaollinen luvulla 8.
Jakoyhtälö
Olkoon \(a\) kokonaisluku ja \(b\) positiivinen kokonaisluku. Tällöin kaikilla \(a\) pätee jakoyhtälö $$a=bq+r,$$ missä \(q\) ja \(r\) ovat kokonaislukuja ja \(0 \leq r < b \).
Esim. 2
Kirjoita jakolaskun \(132:5\) jakoyhtälö.
Esim. 3
Kirjoita jakolaskun \(-132:5\) jakoyhtälö.
2.2 Suurin yhteinen tekijä
Tekijä
Positiivisen kokonaisluvun \(a\) tekijöitä ovat ne positiiviset kokonaisluvut, joilla luku \(a\) on jaollinen.
Suurin yhteinen tekijä
Positiivisten kokonaislukujen \(a\) ja \(b\) suurin yhteinen tekijä on suurin positiivinen kokonaisluku, jolla luvut \(a\) ja \(b\) ovat jaollisia.
Esim. 1
Määritä lukujen \(64\) ja \(36\) suurin yhteinen tekijä tekijöihin jakamalla.
Jakoyhtälö ja syt
Olkoot \(a\) ja \(b\) positiivisia kokonaislukuja. Oletetaan, että \(a=bq+r\), missä \(q\) ja \(r\) ovat positiivisia kokonaislukuja ja \(0< r< b\).
Tällöin pätee \(\text{syt}(a,b)=\text{syt}(b,r)\).
Eukleideen algoritmi
Olkoot \(a\) ja \(b\) positiivisia kokonaislukuja ja \(a>b\). Lukujen \(a\) ja \(b\) suurin yhteinen tekijä saadaan selville alla kuvatulla algoritmilla.
- Muodostetaan jakolaskun \(a:b\) jakoyhtälö \(a=bq_{1}+r_{1}\).
- Jos \(r_{1}>0\), niin muodostetaan jakolaskun \(b:r_{1}\) jakoyhtälö \(b=r_{1}q_{2}+r_{2}\).
- Jos \(r_{2}>0\), niin muodostetaan jakolaskun \(r_{1}:r_{2}\) jakoyhtälö \(r_{1}=r_{2}q_{3}+r_{3}\).
- Jatketaan algoritmin suorittamista, kunnes tulee \(r_{n-1}=r_{n}q_{n+1}+r_{n+1}\), missä \(r_{n+1}=0\) (jako menee tasan).
Viimeinen nollaa suurempi jakojäännös \(r_{n}\) on lukujen \(a\) ja \(b\) suurin yhteinen tekijä.
Esim. 2
Määritä lukujen suurin yhteinen \(261\) ja \(144\) suurin yhteinen tekijä Eukleideen algoritmilla.
Huom.
Murtoluku supistuu yksinkertaisimpaan muotoonsa, kun supistajana on osoittajan ja nimittäjän suurin yhteinen tekijä. Kääntäen, jos osoittajan ja nimittäjän ainoa yhteinen tekijä on 1, murtolukua ei voi supistaa.
Huom.
GeoGebralla suurin yhteinen tekijä voidaan määrittää komennoilla gcd(luku,luku) (greatest common divisor) tai syt(luku,luku).
Myös SpeedCrunchilla voidaan määrittää suurin yhteinen tekijä komennolla gcd(luku;luku) (huomaa erottimena puolipiste).
2.3 Pienin yhteinen monikerta
Pienin yhteinen monikerta
Positiivisten kokonaislukujen \(a\) ja \(b\) pienin yhteinen monikerta, pym (eli pienin yhteinen jaettava, pyj) on pienin positiivinen kokonaisluku, joka on jaollinen luvuilla \(a\) ja \(b\).
Lause
Olkoon \(a\) ja \(b\) positiivisia kokonaislukuja. Tällöin on voimassa $$\text{syt}(a,b)\cdot\text{pym}(a,b)=ab.$$
Esim.
Lavenna samannimisiksi \(\frac{1}{28}\) ja \(\frac{1}{56}\) nimittäjänä pienin mahdollinen positiivinen kokonaisluku.
Huom.
GeoGebralla pienin yhteinen monikerta voidaan määrittää komennoilla lcm(luku,luku) (least common multiple) tai pym(luku,luku).
SpeedCrunch ei määritä pienintä yhteistä monikertaa.
2.4 Kongruenssi
Olkoot \(a\) ja \(b\) kokonaislukuja ja \(n\) lukua yksi suurempi kokonaisluku.
Lukujen \(a\) ja \(b\) sanotaan olevan kongruentteja modulo \(n\), jos erotus \(a-b\) on jaollinen luvulla \(n\).
Toisaalta lukujen \(a\) ja \(b\) kongruenssi modulo \(n\) tarkoittaa, että jaettaessa luvut \(a\) ja \(b\) luvulla \(n\) saadaan sama jakojäännös \(r\).
Kongruenssi merkitään \(a\equiv b\ (\text{mod}\ n)\).
Esim. 1
Luvut \(18\) ja \(6\) ovat kongruentteja modulo \(4\) eli \(18\equiv 6\ \left(\text{mod}\ 4\right)\), koska \(18-6=12\) on jaollinen \(4\):llä, tai toisaalta lukujen \(18\) ja \(6\) yhteinen jakojäännös on \(2\), jos jakana on \(4\).
Jakojäännöksen kongruenssi
Jos jakolaskun \(a:n\) jakojäännös on \(r\), niin \(a\equiv r\ (\text{mod}\ n)\).
Esim. 2
Jakolaskun \(6:4\) jakojäännös on \(2\) eli \(6\equiv 2\ (\text{mod}\ 4)\).
Jakolaskun \(18:4\) jakojäännös on myös \(2\) eli \(18\equiv 2\ (\text{mod}\ 4)\).
Siten luvut \(18\) ja \(6\) ovat kongruentteja keskenään: \(18\equiv 6\ \left(\text{mod}\ 4\right)\).
Huom.
Kongruenssi modulo \(n\) luokittelee kokonaisluvut jäännösluokkiin jakojäännöksen \(0,1,2\ldots,n-1\) mukaan. Luvut, joilla \(n\):llä jaettaessa on sama jakojäännös, kuuluvat samaan luokkaan.
Esim. 3
a) Osoita, että \(289\equiv 25\ (\text{mod}\ 4)\).
b) Mikä on jakojäännös, kun luku \(289\) jaetaan \(4\):llä?
c) Mikä on pienin luonnollinen luku, jonka kanssa \(289\) on kongruentti modulo \(4\)?
Kongruenssin laskusääntöjä
Olkoon \(a\equiv b\ (\text{mod}\ n)\), \(c\equiv d\ (\text{mod}\ n)\) ja \(k\in\mathbb{Z}_{+}\).
1) \(a+c\equiv b+d\ (\text{mod}\ n)\)
2) \(ac\equiv bd\ (\text{mod}\ n)\)
3) \(a^{k}\equiv b^{k}\ (\text{mod}\ n)\)
2.5 Alkuluvut
Alkuluku
Alkuluku on lukua yksi suurempi luonnollinen luku, joka on jaollinen vain luvulla yksi ja itsellään.
Huom.
Alkulukua merkitään usein \(p\) ja alkulukujen joukkoa \(P\) (engl. prime number).
Lukua, joka ei ole alkuluku, kutsutaan yhdistetyksi luvuksi.
Esim. 1
Erastotheneen seula
Luvun osoittaminen alkuluvuksi
Luku \(n\) on alkuluku, jos se ei ole jaollinen millään alkuluvulla, joka on pienempi tai yhtä suuri kuin \(\sqrt{n}\).
Esim. 2
Tutki, onko luku 149 alkuluku.
Aritmetiikan peruslause
Jokainen lukua yksi suurempi kokonaisluku voidaan esittää alkulukujen tulona, ja kullekin luvulle on vain yksi tällainen esitys tekijöiden järjestystä lukuun ottamatta.
Esim. 3
Jaa luku 210 alkutekijöihin.
Huom.
GeoGebralla luvun alkutekijähajotelma saadaan komennoilla factor(luku) tai JaaTekijöihin(luku).
Esim. 4
Määritä alkutekijähajotelman avulla lukujen \(7560\) ja \(8400\) syt ja pym.
3 ALGORITMINEN AJATTELU
3.1 Algoritmi
Algoritmi on niin tarkka kuvaus tai ohje jonkin tietyn prosessin suorittamisesta, että sitä seuraamalla prosessi saadaan suoritetuksi. Ohjelmoinnissa algoritmi kirjoitetaan tietokoneohjelmaksi, jotta kone voi suorittaa prosessin automaattisesti.
Algoritmi voidaan kuvailla sanallisesti esimerkiksi pseudokoodina tai esittää vuokaaviona.
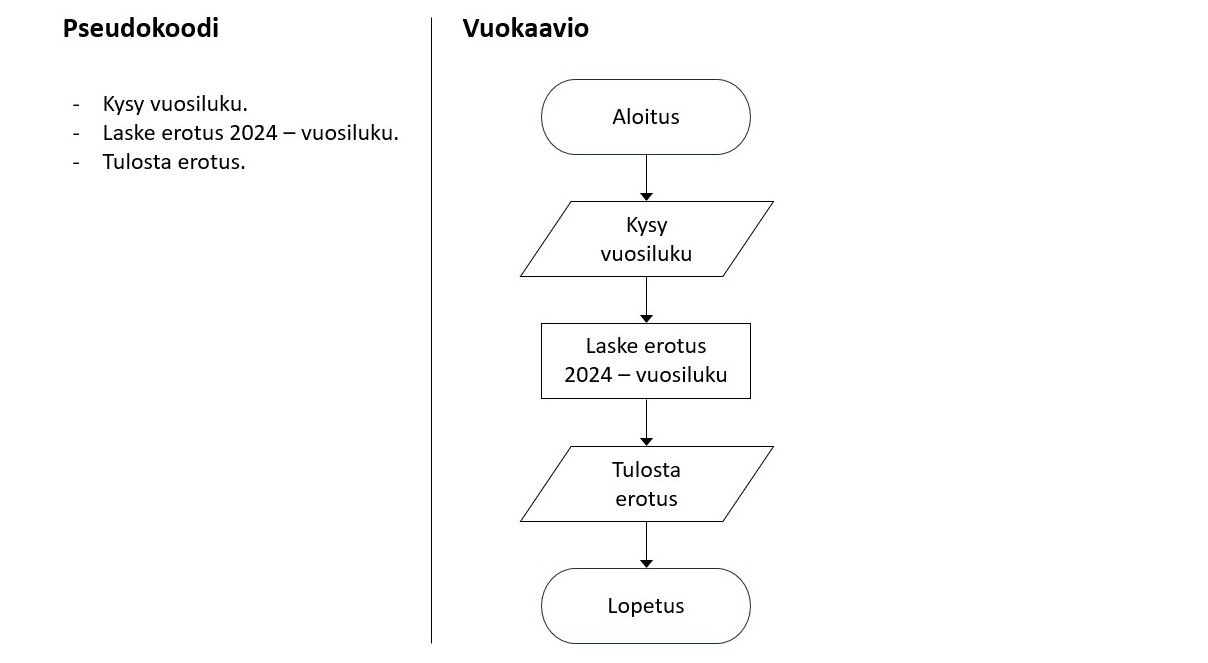
Esim.
Suunnittele ohjelma, joka kysyy käyttäjältä syntymävuoden, lukee sen ja laskee ja tulostaa tiedon siitä, kuinka monta vuotta käyttäjä tänä vuonna täyttää. Laadi ohjelmasta pseudokoodi ja vuokaavio.
Ratkaisu:
3.2 Ohjelmointi
Tällä opintojaksolla käytetään Python-ohjelmointikieltä. Ohjelmat kirjoitetaan Abitin (YTL:n ylläpitämä) verkosta löytyvässä ympäristössä cheat.abitti.fi. Valmiin ohjelman voi kopioida leikepöydälle ja liittää tekstimuotoisena oppikirjan tehtävän vastauskenttään.
Ohjelmointikielillä on syntaksi aivan kuten luonnollisillakin kielillä. Syntaksi määrittää, miten kieltä kirjoitetaan oikein.
Pythonin syntaksin piirteitä:
- Varatut sanat (varattu vain niille tarkoitettuun käyttöön).
- Merkkikokoriippuvainen, engl. case sensitive (iso ja pieni kirjain tulkitaan eri merkkeinä).
- Komentti alkaa #-merkillä.
- Desimaalierottimena piste.
Funktiot
Funktioilla suoritetaan erilaisia toimenpiteitä.
Pythonin funktioita ovat mm.
input()- lukee näppäimistöltä merkkijononprint()- tulostaa tekstin näytöllelen()- laskee merkkijonon pituuden.round()- pyöristää (liuku)luvun.abs()- määrittää itseisarvon.
Muuttujat
Muuttujien avulla kerätään ohjelman käsittelemää tietoa. Ohjelmoija määrittää muuttujat itse syntaksin puitteissa.
Muuttajan arvot voivat olla erityyppisiä. Pythonissa muuttujan tyyppi voidaan määrittää mm. funktioilla
int()- integer, kokonaislukufloat()- floating-point number, liukuluku (desimaaliluku)str()- string, merkkijono.
Esim. 1
Kirjoita ohjelma, joka kysyy käyttäjältä nimen ja tulostaa tervehdyksen ''Hei, nimi!''.
Koodi:
1 nimi=input("Kirjoita nimesi.")
2 print("Hei,", nimi,"!")
Operaattorit
Operaattorien avulla muodostetaan laskutoimituksia, suoritetaan vertailua ja yhdistetään lausekkeita.
Esim. 2
Kirjoita ohjelma, joka kysyy käyttäjältä syntymävuoden, lukee sen ja laskee ja tulostaa tiedon siitä, kuinka monta vuotta käyttäjä tänä vuonna täyttää.
Koodi:
1 vuosi=int(input("Anna syntymävuotesi."))
2 print("Täytät tänä vuonna", 2024-vuosi,"vuotta.")
Esim. 3
Kirjoita ohjelma, joka laskee ja ilmoittaa jakolaskun 5:3 tuloksen kahden desimaalin tarkkuudella.
Koodi:
1 #Tehdään muuttuja ja määritetään sen arvoksi jakolasku 5:3.
2 luku=5/3
3 #Tulostetaan vastaus 2 desimaalin tarkkuudella.
4 print(round(luku,2))
3.3 Valintarakenteet
Ohjausrakenne määrittää ohjelman lauseiden suoritusjärjestyksen. Ohjausrakenteita ovat:
- peräkkäisyys
- valinta
- toisto.
Valintarakenteiden avulla ohjelma voidaan määrittää suorittamaan tietty ohjelman osa vain, jos jokin ehto toteutuu. Ehtoja voidaan esittää vaikkapa vertailuoperaattorien avulla.
Python-ohjelmointikielen valintarakenteita ovat:
- if-rakenne (jos... , niin...)
- if – else -rakenne (jos... , niin... , muutoin...)
- if – elif – else -rakenne (useita tarkistettavia ehtoja).
Huom.
Python-ohjelmointikielen syntaksissa samaan lohkoon kuuluvat ohjelman rivit määritetään sisentämällä ne samaan tasoon.
if-rakenne
Rakenne vastaa luonnollisen kielen rakennetta: "Jos ehto x toteutuu, niin tapahtuu y.''
Ohjelmaksi kirjoitettuna rakenne testaa, onko ehto tosi. Jos ehto on tosi, ohjelma suorittaa ehdon alle kirjoitetun sisennettyjen lauseiden lohkon ja jatkaa seuraavasta sisentämättöstä rivistä. Jos ehto ei ole tosi, ohjelma jatkaa suoraan seuraavaan sisentämättömään riviin.
Esim. 1
Kirjoita ohjelma, joka kysyy käyttäjältä kokonaisluvun ja tutkii, onko luku positiviinen. Jos luku on positiivinen, ohjelma tulostaa ''Luku on positiivinen.''. Lopuksi ohjelma tulostaa ''Loppu.'' merkiksi ohjelman suorittamisesta loppuun.
Koodi:
1 luku=int(input("Anna kokonaisluku."))
2 if luku>0:
3 print("Luku", luku ,"on positiivinen.")
4 print("Loppu.")
if – else -rakenne
Rakenne vastaa luonnollisen kielen rakennetta: "Jos ehto x toteutuu, niin tapahtuu y. Muutoin tapahtuu z.''
Ohjelmaksi kirjoitettuna rakenne testaa, onko ehto tosi. Jos ehto on tosi, ohjelma suorittaa ehdon alle kirjoitetun sisennettyjen lauseiden lohkon. Jos ehto ei ole tosi, ohjelma siirty else-alkuisen rivin alle kirjoitetun sisennettyjen lauseiden lohkon suorittamiseen. Tämän jälkeen ohjelma jatkaa seuraavasta sisentämättömästä rivistä.
Esim. 2
Kirjoita ohjelma, joka kysyy käyttäjältä kaksi kokonaislukua ja tutkii niiden suuruusjärjestystä. Jos ensimmäinen luku on suurempi, ohjelma tulostaa vertailun käyttäen > -merkkiä. Muutoin ohjelma tulostaa vertailun <= -merkillä. Lopuksi ohjelma tulostaa ''Loppu.'' merkiksi ohjelman suorittamisesta loppuun.
Koodi:
1 luku1=int(input("Anna kokonaisluku."))
2 luku2=int(input("Anna toinen kokonaisluku."))
3 if luku1>luku2:
4 print(luku1 ,">", luku2)
5 else:
6 print(luku1, "<=", luku2)
7 print("Loppu.")
Valintarakenteita voidaan kirjoittaa sisäkkäin ja siten testata useita yhtä aikaa voimassa olevia ehtoja taikka useita ehtoja, jotka eivät ole voimassa yhtä aikaa.
Esim. 3
Kirjoita ohjelma, joka kysyy käyttäjältä kokonaisluvun ja tutkii, onko luku positiivinen, nolla vai negatiivinen. Sitten ohjelma ilmoittaa tuloksen. Lopuksi ohjelma tulostaa ''Loppu.'' merkiksi ohjelman suorittamisesta loppuun.
Koodi:
1 luku=int(input("Anna kokonaisluku."))
2 if luku>0:
3 print("Luku", luku, "on positiivinen.")
4 else:
5 if luku<0:
6 print("Luku", luku, "on negatiivinen.")
7 else:
8 print("Luku", luku, "ei ole positiivinen eikä negatiivinen.")
9 print("Loppu.")
if – elif – else -rakenne
Rakenteella voidaan testata useita peräkkäisiä ehtoja, jotka eivät ole yhtä aikaa voimassa.
Ohjelmaksi kirjoitettuna rakenne testaa, onko ehto tosi. Jos ehto on tosi, ohjelma suorittaa ehdon alle kirjoitetun sisennettyjen lauseiden lohkon. Jos ehto ei ole tosi, ohjelma siirtyy testaamaan kunkin elif-alkuisen rivin ehdon. Jos mikään elif-alkuisista ehdoista ei ole tosi, ohjelma testaa else-alkuisen rivin ehdon. Tämän jälkeen ohjelma jatkaa seuraavasta sisentämättömästä rivistä.
Esim. 5
Kirjoita ohjelma, joka tiedustelee käyttäjältä opintojakson pistemäärän ja kertoo käyttäjälle pistemäärää vastaavan arvosanan. Käytä tehtävässä tämän opintojakson pistemäärä-arvosanataulukkoa.
Koodi:
1 luku=int(input("Anna pistemäärä."))
2 if luku>=58:
3 print("Pistemäärää", luku, "vastaava arvosana on 10.")
4 elif luku>=50:
5 print("Pistemäärää", luku, "vastaava arvosana on 9.")
6 elif luku>=42:
7 print("Pistemäärää", luku, "vastaava arvosana on 8.")
8 elif luku>=34:
9 print("Pistemäärää", luku, "vastaava arvosana on 7.")
10 elif luku>=26:
11 print("Pistemäärää", luku, "vastaava arvosana on 6.")
12 elif luku>=18:
13 print("Pistemäärää", luku, "vastaava arvosana on 5.")
14 elif luku>=10:
15 print("Pistemäärää", luku, "vastaava arvosana on 4.")
16 else:
17 print("Pistemäärää", luku, "vastaava arvosana on K.")
18 print("Loppu.")
Python-ohjelmointikielessä ehtoja voidaan yhdistää logiikan konnektiiveja vastaavilla loogisilla operaattoreilla.
Esim. 6
Kirjoita ohjelma, joka kysyy käyttäjältä lukuparin x ja y arvot, lukee ne ja ilmoittaa, mihin koordinaatiston neljännekseen lukuparia vastaava koordinaattipiste kuuluu.
Koodi:
1 x=int(input("Anna luku x:"))
2 y=int(input("Anna luku y:"))
3 if x>0 and y>0:
4 print("Piste (", x,",",y, ") kuuluu koordinaatiston 1. neljännekseen.")
5 elif x<0 and y>0:
6 print("Piste (", x,",",y, ") kuuluu koordinaatiston 2. neljännekseen.")
7 elif x<0 and y<0:
8 print("Piste (", x,",",y, ") kuuluu koordinaatiston 3. neljännekseen.")
9 elif x>0 and y<0:
10 print("Piste (", x,",",y, ") kuuluu koordinaatiston 4. neljännekseen.")
11 else x=0 or y=0:
12 print("Piste (", x,",",y, ") on koordinaattiakselilla.")
13 print("Loppu.")
3.4 Toistorakenteet
Python-ohjelmointikielen toistorakenteita ovat:
- while-rakenne (esiehtoinen toistorakenne)
- for-rakenne (toistojen määrä määräytyy ennalta)
while-rakenne
Python-ohjelmointikielessä on esiehtoinen toistorakenne, while, joka toistaa while-alkuisella rivillä olevan ehdon alle kirjoitettua sisennettyjen rivien lohkoa niin kauan, kuin ehto on tosi. (Python-ohjelmointikielessä ei ole loppuehtoista toistorakennetta.)
Esim. 1
Kirjoita ohjelma, joka tulostaa positiiviset kokonaisluvut annetusta positiivisesta kokonaisluvusta alaspäin.
Koodi:
1 luku=int(input("Anna positiivinen kokonaisluku:"))
2 while luku>0:
3 print(luku)
4 luku=luku-1
Huom.
Edellinen esimerkki voitaisiin toteuttaa myös käyttäen Python-ohjelmointikielen sijoitusoperaattoreita.
Esim. 2
Kirjoita ohjelma, joka tiedustelee käyttäjältä kaksi lukua ja selvittää niiden suurimman yhteisen tekijän Eukleideen algoritmin avulla.
Koodi:
1 print("Ohjelma määrittää kahden kokonaisluvun suurimman yhteisen tekijän Eukleideen algoritmin avulla:")
2 luku1=int(input("Anna ensimmäinen luku:"))
3 luku2=int(input("Anna toinen luku:"))
4 if luku1<luku2:
5 print("Ensimmäisen luvun on oltava suurempi kuin toisen.")
6 else:
7 jakoj=1
8 lukua=luku1
9 lukub=luku2
10 while jakoj!=0:
11 osam=lukua//lukub
12 jakoj=lukua%lukub
13 print(lukua,"=",lukub,"*",osam,"+",jakoj)
14 lukua=lukub
15 lukub=jakoj
16 print("Lukujen",luku1,"ja",luku2,"suurin yhteinen tekijä on:",lukua)
Huom.
Edellisen esimerkin suurin yhteinen tekijä voitaisiin määrittää myös käyttäen math-moduulin gcd()-komentoa. Muita Python-ohjelmointikielen moduuleita on vaikkapa random-moduuli.
for-rakenne
Python-ohjelmointikielessä for-rakenne on toistorakenne, jossa toistojen määrä määräytyy ennakolta.
Merkkijono osoitetaan Python-ohjelmointikielessä lainausmerkeillä. Lista (vrt. lukujono) merkitään hakasulkeiden [ ] sisään. Toistorakenteella for voidaan tulostaa merkkijonon merkit tai listan alkiot (luvut) yksi kerrallaan seuraavasti:
Esim. 1
Kirjoita ohjelma, joka tulostaa sanan abiturientti kirjaimet yksi kerrallaan.
Koodi:
1 merkkijono="abiturientti"
2 for kirjain in merkkijono:
3 print(kirjain)
Esim. 2
Kirjoita ohjelma, joka tulostaa kokonaisluvut yhdestä neljään.
Koodi:
1 lista=[1,2,3,4]
2 for luku in lista:
3 print(luku)
Listan paikkanumerointi eli indeksointi alkaa Python-ohjelmointikielessä luvusta 0.
Esim. 3
Kirjoita ohjelma, joka tulostaa listan kolmannen luvun.
Koodi:
1 lista=[1,2,3,4]
2 print([2])
Huom.
Listan alkiot voivat olla lukujen lisäksi myös merkkijonoja tai listoja listan sisällä.
Python-ohjelmointikielessä for-rakennetta voidaan ohjata funktion range(alkuarvo,loppuarvo,askel) avulla.
Esim. 4
Kirjoita ohjelma, joka tulostaa parilliset kokonaisluvut nollasta kymmeneen.
Koodi:
1 for n in range(0,11,2):
2 print(n)
Huom.
- Suuruusjärjestys suuremmasta pienempää saadaan asettamalla askeleeksi negatiivinen luku.
- Jos annetaan vain kaksi parametria, Python tulkitseen ne alku- ja loppuarvoksi ja käyttää oletuksena askel=1.
- Jos annetaan vain yksi parametri, Python tulkitseen sen loppuarvoksi ja käyttää oletuksena alkuarvo=0 ja askel=1.
3.5 Lukujärjestelmät
Käytössämme oleva lukujärjestelmä on kymmenjärjestelmä eli desimaalijärjestelmä. Järjestelmä on paikkajärjestelmä, jonka kantaluku on \(10\). Kaikki luvut voidaan ilmaista kymmenen numeromerkin \((0,1,2,3,4,5,6,7,8,9)\) avulla. Numeron paikka luvussa ilmaisee paikkaa vastaavan kymmenpotenssin lukumäärän. Luku on näiden kymmenpotenssien summa.
Esim. 1
$$2\ 834{,}15=2\cdot10^{3}+8\cdot10^{2}+3\cdot10^{1}+4\cdot10^{0}+1\cdot10^{-1}+5\cdot10^{-2}$$
Ihmiskunnan historiassa on ollut käytössä erilaisia lukujärjestelmiä, joissa lukujen merkitsemistapa ja myös kantaluku ovat vaihdelleet. Lukujärjestelmän kantaluku voidaankin valita vapaasti. Nykyään erityisesti tietoteknisissä sovelluksissa hyödynnetäänkin kaksi- eli binääri-, kahdeksan- eli oktaali- ja kuusitoista- eli heksadesimaalijärjestelmiä.
Kaksijärjestelmässä kantaluku on kaksi ja luvut ilmaistaan numeromerkeillä \(0\) ja \(1\).
Esim. 2
a) Muunna kaksijärjestelmän luku \(1011\) kymmenjärjestelmän luvuksi.
b) Muunna kymmenjärjestelmän luku \(19\) kaksijärjestelmän luvuksi.
Huom.
Esimerkin 2 b-kohdan muunnos voidaan suorittaa laskemalla jakoyhtälöiden jakojäännökset. Viimeinen jakojäännös on luvun ensimmäinen numero, toiseksi viimeinen toinen jne.
Kahdeksanjärjestelmässä luvut ilmaistaan numeromerkeillä \(0,\dots,7\) ja kuusitoistajärjestelmässä numeromerkeillä \(0,\dots,9\) sekä kirjaimilla \(A,\dots,F\).
Esim. 3
Kuusitoistajärjestelmässä lukua kymmenen vastaa \(A_{16}\), lukua \(15_{10}\) vastaa \(F_{16}\) ja lukua \(16_{10}) vastaa \(10_{16}\) jne.
3.6 Numeerinen ratkaiseminen
Aina ei ole keinoa selvittää yhtälön ratkaisulle tarkkaa arvoa. Yhtälön ratkaisun likiarvo voidaan kuitenkin määrittää numeerisesti
- puolitusmenetelmällä
- kiintopistemenetelmällä
Puolitusmenetelmä
Puolitusmenetelmä perustuu Boltzanon lauseeseen, jonka mukaan jatkuvalla funktiolla on suljetulla välillä ainakin yksi nollakohta, jos funktion arvot välin päätepisteissä ovat erimerkkiset.
Esim.
Määritetään funktion \(f(x)=3x-2^{x}\) välillä \(\left[0,1\right]\) olevan nollakohdan likiarvo yhden desimaalin tarkkuudella taulukoimalla.
$$ \begin{array}{l|l|l} \text{Funktion arvo}&\text{Väli}&\text{Välin keskipiste}\\ \hline f(0)=-1\lt0&&\\ f(1)=1\gt0&\left]0,1\right[&0{,}5\\ f(0{,}5)=0{,}085\ldots\gt0&\left]0;0{,}5\right[&0{,}25\\ f(0{,}25)=-0{,}439\ldots\lt0&\left]0{,}25;0{,}5\right[&0{,}375\\ f(0{,}375)=-0,171\ldots\lt0&\left[0{,}375;0{,}5\right[&0{,}4375\\ f(0{,}4375)=-0{,}041\ldots\lt0&\left]0{,}4375;0{,}5\right[&0{,}46875\\ f(0{,}46875)=0{,}022\ldots\gt0&\left]0{,}4375;0{,}46875\right[&0{,}453125\\ f(0{,}453125)=-0{,}009\ldots\lt0&\left]0{,}453125;0{,}46875\right[& \end{array} $$
Viimeisen välin päätepisteet pyöristyvät yhden desimaalin tarkkuudella samaan lukuun \(0{,}5\). Siis nollakohta on \(x\approx0{,}5.\)
Kiintopistemenetelmä
Kiintopistemenetelmä perustuu iterointiin. Iterointi tarkoittaa saman toimenpiteen toistamista aina uudelleen.
Muuttujan arvoa \(x=a\), jolla funktion arvo on \(f(a)=a\), kutsutaan funktion \(f\) kiintopisteeksi.
Kiintopistemenetelmällä voidaan löytää muotoa \(x=f(x)\) olevan yhtälön ratkaisu \(x=a\), mikäli funktion kuvaaja ei ole kiintopisteen kohdalla liian jyrkkä ja alkuarvo iteroinnille valitaan riittävän läheltä kiintopistettä.
Esim.
Etsi kiintopistemenetelmällä yhtälön \(x^{3}-2x-7=0\) ainoalle ratkaisulle kaksidesimaalinen likiarvo käyttämällä alkuarvoa \(x_{1}=2\).