Pitkän matematiikan kertaus (MAA20)
Laajuus
2 op
Yleiset tavoitteet (Kuopion lukioiden OPS 2021)
Moduulin tavoitteena on, että opiskelija
- valmentautuu ylioppilaskirjoituksiin
- saa valmiuksia jatko-opintoihin ja tulevaisuuden työelämään.
Keskeiset sisällöt (Kuopion lukioiden OPS 2021)
- kerrataan ja syvennetään lukion pitkän matematiikan oppimäärän keskeisiä sisältöjä.
Aikataulu
Suoritus
- osallistuminen
- tehtävien tekeminen
- vähintään lämmittelysarja ja yksi asianmukaisesti tehty annettu tehtävä kustakin oppikirjan kappaleesta 1-16
- preli
Arviointi
- ''Opiskelijan arviointi kohdistuu matematiikalle ominaisen vastaustekniikan hallintaan ja aihesisältöjen osaamiseen. Asiasisältöjen hallintaa arvioidaan opiskelijan opintojakson aikana tekemien harjoitustehtävien kautta. Opintojakson päätteeksi voidaan pitää YO-koetta vastaava laaja harjoituskoe. Arviointikriteerit pohjautuvat YTL:n hyvän vastauksen piirteisiin.'' (Kuopion lukioiden OPS 2021)
- arvosana S/K
Keskeyttäminen
Opettaja keskeyttää opiskelijan opintojakson, jos
- opiskelija niin pyytää
- opiskelija ei ole läsnä opintojakson kahdella ensimmäisellä opetuskerralla ja opiskelija ei ole yhteydessä opettajaan eikä opettaja saa yhteyttä opiskelijaan.
Opettaja voi keskeyttää opiskelijan opintojakson, jos opiskelijalla on neljä (4) poissaoloa. Tällaiset tilanteet opettaja käy läpi tapauskohtaisesti ja on ennen lopullista keskeytystä yhteydessä opiskelijaan.
Keskeyttämisestä opettaja merkitsee opintojaksosta opiskelijalle K-merkinnän Wilmaan ja poistaa opiskelijan sen jälkeen Wilman ryhmästä. Opettaja lähettää keskeyttämisestä viestin opiskelijalle, alaikäisen opiskelijan huoltajalle, ryhmänohjaajalle ja opolle.
1 VALMISTAUTUMINEN YO-KOKEESEEN
1.1 Kokeen rakenne
Pitkän matematiikan koe jakaantuu A-osaan sekä B1- ja B2-osaan.
A-osassa kokelas vastaa kuudesta tehtävästä viiteen. A-osassa ei ole käytössä GeoGebraa eikä taulukkolaskentaohjelmaa. Peruslaskimista käytössä ovat mm. Abicus ja SpeedCrunch (jälkimmäinen vain kevääseen 2026 asti). Taulukot ovat käytössä myös A-osassa.
B1-osassa kokelas vastaa neljästä tehtävästä kolmeen ja B2-osassa kolmesta tehtävästä kahteen.
Yhteensä kokeessa on siis 13 tehtävää, joista vastataan kymmeneen. Kukin tehtävä on 12 pisteen arvoinen. Siten kokeen enimmäispistemäärä on 120 pistettä.
Huom. Kaikkiin tehtäviin on mahdollista vastata kokeen alusta alkaen. Ainoastaan laskinohjelmistot vapautuvat käyttöön vasta, kun A-osa on palautettu.
1.2 Kokeeseen tutustuminen
Ennen kuin aloittaa vastaamaan yhteenkään tehtävään, kannattaa käyttää hetki aikaa kokeeseen tutustumiseen ja suunnitella vastaamisjärjestys.
Kokeen rakenteesta saa yleiskuvan sisällysluettelon avulla. Sisällysluettelosta näkee, liittyykö johonkin tehtävään aineistoja.
Voi olla suositeltavaa lukea myös tehtävät aluksi läpi.
Vastaaminen kannattaa aloittaa helpoimmista tehtävistä.
Karkeasti voi arvioida, että jokaista tehtävää kohti on käytössä noin puoli tuntia aikaa.
1.3 Vastauksen laatiminen
Alle on koottu ylioppilastutkintolautakunnan opettajille alustavaa arvostelua antamia ohjeita (lähde: ylioppilastutkinto.fi, 22.10.2025).
''Hyvästä suorituksesta näkyy, miten vastaukseen on päädytty. Ratkaisussa on oltava tarvittavat laskut tai muut riittävät perustelut sekä lopputulos. Arvioinnissa kiinnitetään huomiota kokonaisuuteen, ja ratkaisu pyritään arvioimaan kolmiosaisesti: alku, välivaiheet ja lopputulos. Laskuvirheet, jotka eivät olennaisesti muuta tehtävän luonnetta, eivät alenna pistemäärää merkittävästi. Sen sijaan tehtävän luonnetta muuttavat lasku- ja mallinnusvirheet saattavat alentaa pistemäärää huomattavasti.''
''Matemaattiset ohjelmistot ovat kokeen apuvälineitä, joiden roolit arvioidaan tehtäväkohtaisesti. Jos ratkaisussa on käytetty ohjelmistoja, sen on käytävä ilmi suorituksesta. Analysointia vaativien tehtävien ratkaisemisessa pelkkä ohjelmistolla saatu vastaus ei riitä ilman muita perusteluja. Sen sijaan ohjelmasta saatu tulos yleensä riittää rutiinitehtävissä ja laajempien tehtävien rutiiniosissa. Tällaisia ovat esimerkiksi lausekkeiden muokkaaminen, yhtälöiden ratkaiseminen sekä funktioiden derivointi ja integrointi.''
Erilaisia pistevähennykseen johtavia puutteita vastauksessa:
- Vastaus oikein, muttei pyydetyssä muodossa (esimerkiksi tarkkuus, yksikkö) -1 p.
- Vastaus sieventämättä loppuun asti sievennystehtävässä (esimerkiksi \(e^1\), \(\ln e\) tai \(4^0\)) -2 p.
- Vastaus sieventämättä muussa tehtävässä (esimerkiksi \(e^1\), \(\ln e\) tai \(4^0\)) -1 p.
- Ilmeiset näppäilyvirheet esityksessä (esimerkiksi \(x=2, y04\)), tai näppäilyvirheet, jotka korjataan heti seuraavalla rivillä -0 p.
- Vastauksessa kopiointivirhe -1 p.
- Välipyöristyksessä ei yhtä enemmän merkitseviä numeroita kuin vastauksessa -1 p.
- Matemaattisesti puutteellinen merkintä (esimerkiksi puuttuvat sulut, mutta laskettu oikein; \(=\) -merkin ketjutus, \(\text{m}^2\) ilman \(\text{m}\)). Huom.! Tilanteesta riippuen epästandardi merkintä voidaan hyväksyä selitettynä. -1 p.
- Ratkaisusta puuttuu oleellisia selityksiä (lukija joutuu arvaamaan, mitä ratkaisussa esiintyvät luvut tarkoittavat) TAI perustelut ja johtopäätökset on esitetty täysin irrallisina (lukija joutuu yhdistelemään eri puolilla ratkaisua olevia lauseita) -1 p.
- Ratkaisussa merkittävästi ylimääräistä tekstiä/laskuja (lukija joutuu päättelemään, miten annetuista tiedoista muodostuu ratkaisu) -1 p.
1.4 Lukusuunnitelma
Kolmannen jakson lopusta ylioppilaskokeiden alkuun on viisi kokonaista viikkoa. Riippuen lukujärjestyksistä ja keväällä kirjoitettavista aineista väli voi olla pidempikin. Tuon ajan hyödyntämisessä parhaalla mahdollisella tavalla voi auttaa lukusuunnitelma.
Ohjeita lukusuunnitelman laatimiseen
Tee lukusuunnitelma konkreettisesti paperille tai kalenteriin.
Merkitse ensin pakolliset menot.
Merkitse sitten ajat, jotka voit käyttää opiskeluun.
Jos mahdollista, luo rutiineja. Esimerkiksi aloitus ja ruokatauko aina samaan aikaan.
Varaa vaikeimmalle aineelle eniten aikaa.
Jos opiskelet yli kaksi tuntia päivässä, voit opiskelle kahta ainetta. Aloita vaikeammasta, jolloin olet todennäköisesti virkeimmilläsi.
Opiskele jokaista ainetta vähintään kahdesti viikossa.
Vuorottele etenemistä ja kertaamista.
Muista tauotus ja palautuminen.
Pysy suunnitelmassa, mutta ole valmis muuttamaan suunnitelmaa tarvittaessa.
Matematiikkaa oppii laskella. Kertaamisessa voi hyödyntää esimerkiksi oppikirjojen esimerkkitehtäviä.
1.5 Laskimet
Abicus on hyvä peruslaskin.
SpeedCrunch on käytössä vain kevääseen 2026 asti.
GeoGebra mahdollistaa yhtälönratkaisun ja muita vaativampia operaatioita.
Muista myös taulukkolaskenta.
Muitakin laskimia saa käyttää, jos osaa.
2 FUNKTIOT JA YHTÄLÖT 1
2.1 Laskutoimituksia
Esim. 1
Laske tai sievennä ilman laskinta.
a) \(-3\dfrac{1}{5}:\dfrac{4}{25}\)
b) \(\dfrac{x^{5}y^{4}}{x(x^{2}y)^{3}}\)
c) \(\sqrt{x}\left(\sqrt{x}-\dfrac{\sqrt{x^{3}}}{x}\right)\)
a) \(-3\dfrac{1}{5}:\dfrac{4}{25}\)
\(\quad=-\dfrac{16}{5}:\dfrac{4}{25}\)
\(\quad=-\dfrac{16}{5}\cdot\dfrac{25}{4}\)
\(\quad=-\dfrac{4}{1}\cdot\dfrac{5}{1}\)
\(\quad=-\dfrac{20}{1}\)
\(\quad=-20\)
b) \(\dfrac{x^{5}y^{4}}{x(x^{2}y)^{3}}\)
\(\quad=\dfrac{x^{5}y^{4}}{x(x^{2})^{3}y^{3}}\)
\(\quad=\dfrac{x^{5}y^{4}}{xx^{6}y^{3}}\)
\(\quad=\dfrac{x^{5}y^{4}}{x^{7}y^{3}}\)
\(\quad=x^{-2}y\)
\(\quad=\dfrac{y}{x^{2}}\)
c) \(\sqrt{x}\left(\sqrt{x}-\dfrac{\sqrt{x^{3}}}{x}\right)\quad(,\ x\ge0)\)
\(\quad=\sqrt{x}\sqrt{x}-\sqrt{x}\dfrac{\sqrt{x^{3}}}{x}\)
\(\quad=\sqrt{x^{2}}-\dfrac{\sqrt{x^{4}}}{x}\)
\(\quad=\left|x\right|-\dfrac{\sqrt{\left(x^{2}\right)^{2}}}{x}\)
\(\quad=x-\dfrac{\left|x^{2}\right|}{x}\)
\(\quad=x-\dfrac{x^{2}}{x}\)
\(\quad=x-x\)
\(\quad=0\)
Esim. 2 (yo, m, 1.1/2025S)
Valitse oikea vaihtoehto.
- Kuinka paljon on 12 prosenttia luvusta 34? (2 p.)
Esim. 3 (yo, m, 1.2/2024S)
Kirjoita tämän tehtävän vastauskenttiin pelkät laskujen lopputulokset ilman välivaiheita ja perusteluja. Jokaisen osatehtävän vastaus on kokonaisluku.
- Laske (2 p.)
Harrin palkka on 4 200 euroa kuukaudessa. Hänen palkastaan vähennetään 33 % ennakonpidätystä, joka sisältää pakolliset eläke- ja työttömyysvakuutusmaksut. Harrin nettopalkka euron tarkkuudella oneuroa .
Esim. 4 (yo, m, 1.4/2024S)
Kirjoita tämän tehtävän vastauskenttiin pelkät laskujen lopputulokset ilman välivaiheita ja perusteluja. Jokaisen osatehtävän vastaus on kokonaisluku.
- Laske (2 p.)
Kokeiden arvostelu kestää kolmelta opettajalta yhteensä 12 tuntia. Neljältä opettajalta samaan urakkaan menisi tuntia. Jokainen opettaja arvostelee kokeensa itsenäisesti ja samalla nopeudella.
2.2 Potenssifunktio
Esim. 1 (yo, m, 2.1&4/2024K)
Kirjoita tämän tehtävän vastauskenttiin pelkät laskujen lopputulokset ilman välivaiheita ja perusteluja. Jokaisen kohdan vastaus on kokonaisluku.
- Laske polynomin \(p(x)=12x^{3}+4x\) arvo kohdassa \(x=2\). (3 p.)
- Määritä neljännen asteen termin kerroin polynomissa \((12x^{3}+4x)^{2}\). (3 p.)
Esim. 2 (yo, m, 1/2020S)
Yhtälöitä (12 p.)
- Millä luvun \(x\) arvolla yhtälö \(\dfrac{x+1}{2}+\dfrac{2x-1}{4}=\dfrac{x}{2}\) on tosi? (3 p.)
\(x=\) - Millä vakion \(a\) arvolla yhtälö \((x+a)(x-a)=x^{2}-81\) on tosi kaikilla reaaliluvuilla \(x\)? (3 p.)
\(a=\) - Mikä seuraavista vaihtoehdoista pätee yhtälöön \(2(x-1)=3x-(x+1)\)? (3 p.)
- Määritä sellainen luku \(b\), että piste \((-7,b)\) on suoralla \(6x+4y=2\). (3 p.)
\(b=\)
Esim. 3 (yo, m, 1/2023S)
Yhtälö ja epäyhtälö (12 p.)
- Ratkaise yhtälö \(-7x+3=17\). (3 p.)
- Ratkaise epäyhtälö \(-7x+3\lt17\). (3 p.)
- Ratkaise yhtälö \(x^{2}+x=2\). (3 p.)
- Ratkaise epäyhtälö \(x^{2}+x-2\le0\). (3 p.)
Esim. 4 (yo, m, 1.1-2/2025K)
Anna tässä tehtävässä pelkkä vastaus ilman perusteluja. Vastauskenttään voi kirjoittaa vain yhden kokonaisluvun.
- Ratkaise yhtälö \(5x-17=43\). (2 p.)
- Ratkaise potenssiyhtälö \(2x^{3}-128=0\). (2 p.)
Esim. 5 (yo, m, 3/2025S)
Epäyhtälö ja yhtälö (12 p.)
Ratkaise epäyhtälö \((x-1)(x+3)\gt-3\). (6 p.)
Ratkaise yhtälö \((x+e)(x^{2}-\pi^{2})=0\). (6 p.)
2.3 Rationaalifunktio
Esim. 1 (yo, m, 2.1/2025K)
Sievennyksiä (12 p.)
- Sievennä lauseke \(\dfrac{(y^{2}-4)(y+1)}{(y-2)}\), kun \(y\neq2\). (6 p.)
- Sievennä lauseke \(\sqrt{(z-1)^{2}+2(z-1)+1}\). (6 p.)
Kohta 1:
\(\dfrac{(y^{2}-4)(y+1)}{(y-2)}\)
\(=\dfrac{(y^{2}-2^{2})(y+1)}{(y-2)}\)
\(=\dfrac{(y+2)\cancel{(y-2)}(y+1)}{\cancel{(y-2)}}\)
\(=y^{2}+y+2y+2\)
\(=y^{2}+3y+2\), kun \(y\neq2\)
Esim. 2 (yo, m, 3.1/2021K)
- Osoita, että yhtälö $$\dfrac{4}{4-x^{2}}=\dfrac{1}{2+x}+\dfrac{1}{2-x}$$ on voimassa kaikilla \(x\neq\pm2\). (4 p.)
Esim. 3
Määritä rationaalifunktion \(\displaystyle{f(x)=\frac{x^2+2x+1}{x^2-4}}\) nollakohdat.
Määrittelyehto:
Nimittäjän nollakohdat
\(\begin{alignat}{3} x^2-4&=0 \quad \mid +4\\ x^2&=4 \quad \mid\ \sqrt{\ }\\ x&=\pm2 \end{alignat}\)
Rationaalifunktio \(f\) on määritelty, kun \(x\neq-2\) ja \(x\neq2\).
Funktion \(f\) nollakohdat
\(\begin{alignat}{3} f(x)&=0\\ \\ \displaystyle{\frac{x^2+2x+1}{x^2-4}}&=0 &\mid \cdot\ (x^2-4)\\ \\ x^2+2x+1&=0\\ \\ x&=\displaystyle{\frac{-2\pm\sqrt{2^2-4\cdot1\cdot1}}{2\cdot1}}\\ \\ &=\displaystyle{\frac{-2\pm\sqrt{4-4}}{2}}\\ \\ &=\displaystyle{\frac{-2\pm\sqrt{0}}{2}}\\ \\ &=\displaystyle{\frac{-2}{2}}\\ \\ x&=-1 \end{alignat}\)
Toteuttaa määrittelyehdon.
Vastaus: \(x=-1\)
2.4 Juurifunktio
Esim. 1 (yo, m, 2.2/2025K)
Sievennyksiä 12 p.
- Sievennä lauseke \(\dfrac{(y^{2}-4)(y+1)}{(y-2)}\), kun \(y\neq2\). (6 p.)
- Sievennä lauseke \(\sqrt{(z-1)^{2}+2(z-1)+1}\). (6 p.)
Kohta 2:
\(\sqrt{(z-1)^{2}+2(z-1)+1}\)
\(=\sqrt{((z-1)+1)^{2}}\)
\(=\left|z-1+1\right|\)
\(=\left|z\right|\)
Esim. 2
Ratkaise yhtälö.
a) \(\sqrt[3]{2x^2-8}-4=0\)
b) \(\sqrt[4]{2x+2}=\sqrt[4]{x^2-1}\)
3 GEOMETRIA
3.1 Tasogeometria
Esim. 1 (yo, m, 1/2024K)
Kulmanmetsästys 12 p.
Määritä kuviin merkityt tuntemattomat kulmat asteen tarkkuudella.
Kirjoita tämän tehtävän vastauskenttiin pelkät laskujen lopputulokset ilman välivaiheita ja perusteluja. Jokaisen kohdan vastaus on kokonaisluku.
Määritä kulma \(\alpha\). (2 p.)
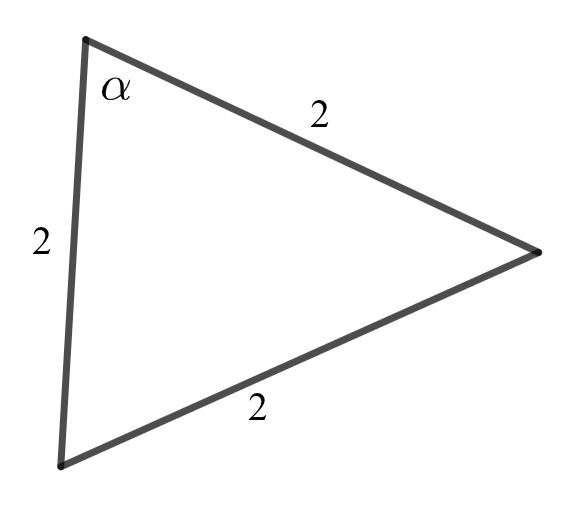
\(\alpha=\) astetta
Määritä kulma \(\beta\). (2 p.)
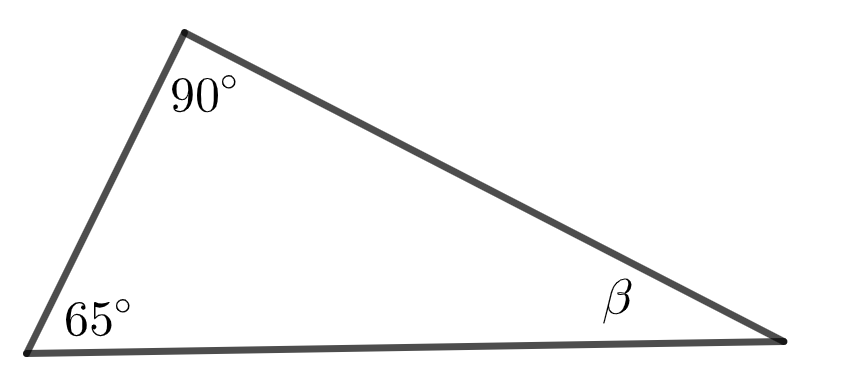
\(\beta=\) astetta
Määritä kulma \(\gamma\). (2 p.)
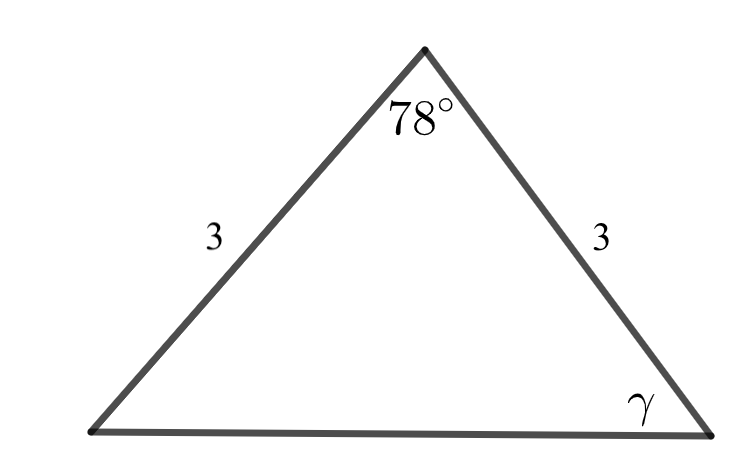
\(\gamma=\) astetta
Määritä kulma \(\delta\). (2 p.)
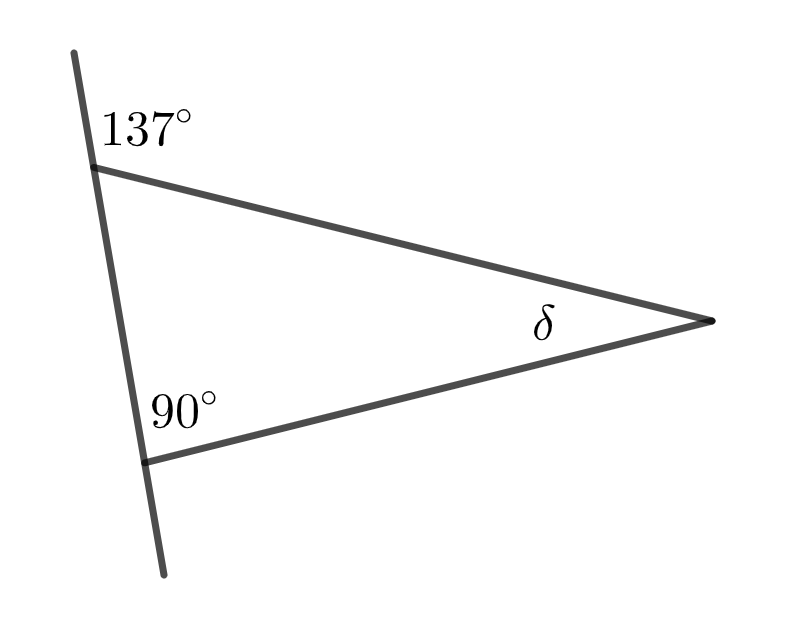
\(\delta=\) astetta
Määritä kulma \(\epsilon\). (2 p.)
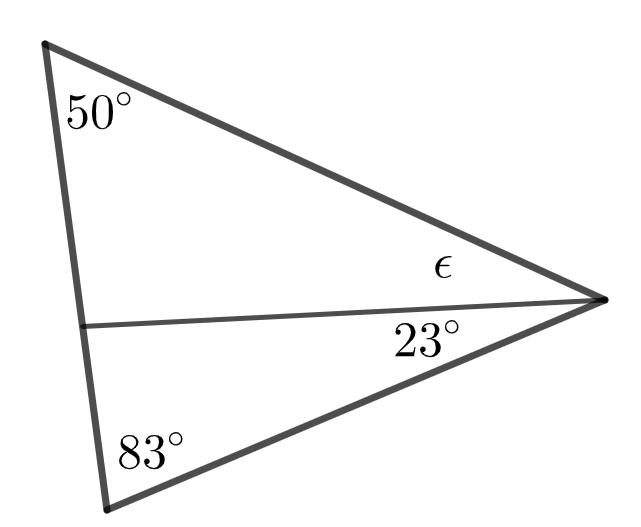
\(\epsilon=\) astetta
Määritä kulma \(\zeta\). (2 p.)
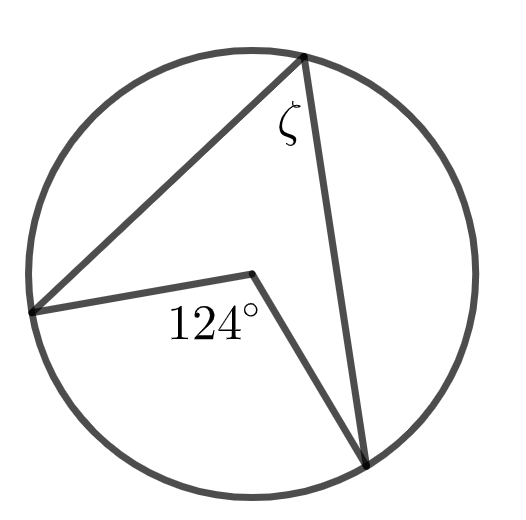
\(\zeta=\) astetta
- 60
- 25
- 51
- 47
- 24
- 62
Esim. 2 (yo, m, 7.1-2/2025S)
Geometrian laskutehtäviä 12 p.
Anna tässä tehtävässä pelkkä vastaus ilman perusteluja. Vastauslaatikkoon voi kirjoittaa vain yhden kokonaisluvun.
Laske kussakin osatehtävässä tuntemattoman likiarvo kokonaisluvuksi pyöristettynä.
Kolmion kärjet ovat pisteissä \((12, 3)\), \((-2, 9)\) ja \((4, 20)\), ja sen pinta-ala on \(A_1\). (2 p).
\(A_1\approx\)
Kolmion kärjet ovat pisteissä \((12, 3)\), \((-2, 9)\) ja \((4, 20)\), ja sen piirin pituus on \(p\). (2 p.)
\(p\approx\)
Suoran ympyrälieriön korkeus on \(13\), säde \(4\) ja vaipan pinta-ala \(A_2\). (2 p.)
\(A_2\approx\)
Pisteen \((-20, 6)\) etäisyys suorasta \(2x+y+5=0\) on \(d\). (2 p.)
\(d\approx\)
Olkoot \(\bar{u}=\bar{i}+2\bar{j}\) ja \(\bar{v}=2\bar{i}-2\bar{j}\). Vektorien \(\bar{u}\) ja \(\bar{v}\) välinen kulma asteina on \(\alpha\). (2 p.)
\(\alpha\approx\)
Olkoot \(\bar{u}\) ja \(\bar{v}\) kuten osatehtävässä 7.5. Vektorin \(4\bar{u}-7\bar{v}\) pituus on \(L\). (2 p.)
\(L\approx\)
Esim. 3 (yo, m, 3/2025K)
Suorakulmaiset kolmiot 12 p.
3.A Kuva: Hahmotelma kolmioista
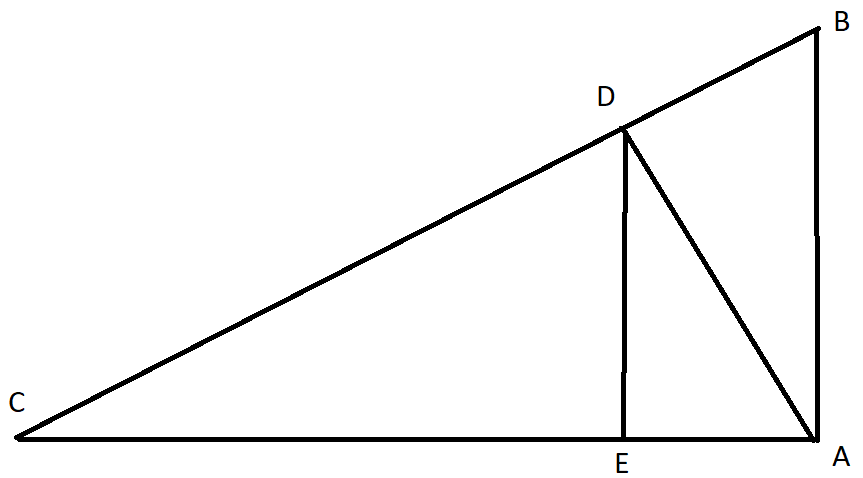
Lähde: YTL.
Suorakulmaisen kolmion \(ABC\) sivujen pituudet ovat \(\left|AB\right|=3\), \(\left|AC\right|= 4\) ja \(\left|BC\right|=5\). Suorasta kulmasta \(A\) piirretään korkeusjana kohtisuoraan hypotenuusalle pisteeseen \(D\). Pisteestä \(D\) piirretään edelleen kohtisuora jana kateetille \(AC\) pisteeseen \(E\). Lopputulos on hahmoteltu kuvassa 3.A.
Määritä suorakulmaisen kolmion \(ADE\) kateettien pituudet.
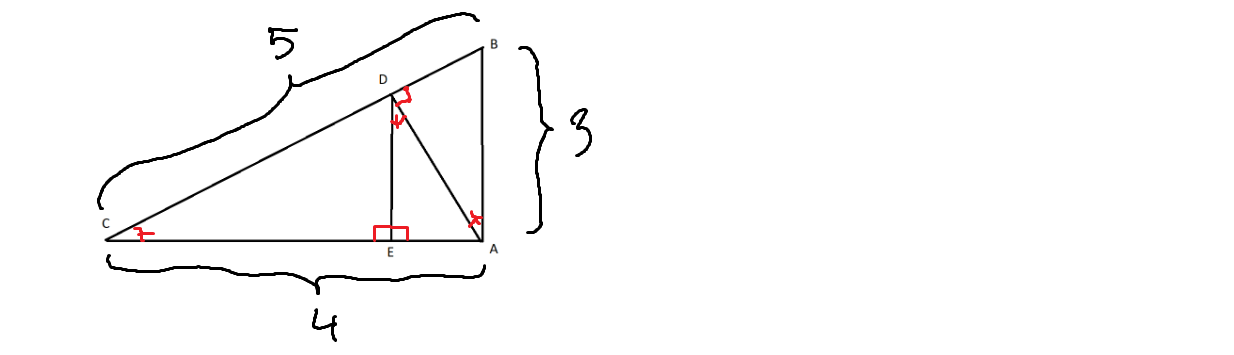
Suorakulmaiset kolmiot \(ABC\) ja \(ACD\) ovat yhdenmuotoiset kk-lauseen perusteella, koska kolmioilla on yhteisenä \(\sphericalangle C\).
Yhdenmuotoisuuden perusteella:
\(\begin{align} \dfrac{\left|AD\right|}{\left|AB\right|}&=\dfrac{\left|AC\right|}{\left|BC\right|}\\ \\ \dfrac{\left|AD\right|}{\left|3\right|}&=\dfrac{\left|4\right|}{\left|5\right|}\\ \\ \left|AD\right|&=\dfrac{3\cdot4}{5}=\dfrac{12}{5} \end{align}\)
Koska sivut \(AB\) ja \(DE\) ovat yhdensuuntaiset, niin \(\sphericalangle BAD\) ja \(\sphericalangle EDA\) ovat samankohtaisina kulmina yhtä suuret. Siten suorakulmaiset kolmiot \(ABC\) ja \(ADE\) ovat kk-lauseen perusteella yhdenmuotoiset.
Yhdenmuotoisuuden perusteella:
\(\begin{align} \dfrac{\left|DE\right|}{\left|AC\right|}&=\dfrac{\left|AD\right|}{\left|BC\right|}\\ \\ \dfrac{\left|DE\right|}{4}&=\dfrac{\frac{12}{5}}{5}\\ \\ \left|DE\right|&=\dfrac{4\cdot\frac{12}{5}}{5}=\dfrac{48}{25} \end{align}\)
ja
\(\begin{align} \dfrac{\left|AE\right|}{\left|AB\right|}&=\dfrac{\left|AD\right|}{\left|BC\right|}\\ \\ \dfrac{\left|AE\right|}{3}&=\dfrac{\frac{12}{5}}{5}\\ \\ \left|AE\right|&=\dfrac{3\cdot\frac{12}{5}}{5}=\dfrac{36}{25} \end{align}\)
Vastaus: Kolmion \(ADE\) kateettien pituudet ovat \(\frac{36}{25}(=1{,}44)\) ja \(\frac{48}{25}(=1{,}92)\).
3.2 Avaruusgeometria
Esim. 1 (yo, m, 7.3/2025S)
Geometrian laskutehtäviä 12 p.
Anna tässä tehtävässä pelkkä vastaus ilman perusteluja. Vastauslaatikkoon voi kirjoittaa vain yhden kokonaisluvun.
Laske kussakin osatehtävässä tuntemattoman likiarvo kokonaisluvuksi pyöristettynä.
Kolmion kärjet ovat pisteissä \((12, 3)\), \((-2, 9)\) ja \((4, 20)\), ja sen pinta-ala on \(A_1\). (2 p).
\(A_1\approx\)
Kolmion kärjet ovat pisteissä \((12, 3)\), \((-2, 9)\) ja \((4, 20)\), ja sen piirin pituus on \(p\). (2 p.)
\(p\approx\)
Suoran ympyrälieriön korkeus on \(13\), säde \(4\) ja vaipan pinta-ala \(A_2\). (2 p.)
\(A_2\approx\)
Pisteen \((-20, 6)\) etäisyys suorasta \(2x+y+5=0\) on \(d\). (2 p.)
\(d\approx\)
Olkoot \(\bar{u}=\bar{i}+2\bar{j}\) ja \(\bar{v}=2\bar{i}-2\bar{j}\). Vektorien \(\bar{u}\) ja \(\bar{v}\) välinen kulma asteina on \(\alpha\). (2 p.)
\(\alpha\approx\)
Olkoot \(\bar{u}\) ja \(\bar{v}\) kuten osatehtävässä 7.5. Vektorin \(4\bar{u}-7\bar{v}\) pituus on \(L\). (2 p.)
\(L\approx\)
Esim. 2 (yo, m, 6/2023S)
Appelsiinien kuoret 12 p.
Kaupassa myydään kokonaisia appelsiineja 1,50 euron kilohinnalla ja kuorittuja appelsiineja 9,50 euron kilohinnalla. Kuorimattomien appelsiinien ympärysmitta on 25,0 cm ja kuoren paksuus 6,0 mm.
Kuinka suuri osuus appelsiinin tilavuudesta on kuorta? Oletetaan appelsiini palloksi ja kuori tasapaksuksi. (6 p.)
Mikä on kuorimistyön osuus hinnasta prosentteina? Oletetaan, että kuoren ja syötävän osan tiheys on sama ja että kuoren arvo on nolla euroa. (6 p.)
Määritetään kuorimattomien appelsiinien säde ja tilavuus.
Säde:
\(\begin{align} p&=2\pi r_1\\ r_1&=\dfrac{p}{2\pi}\\ r_1&=\dfrac{25{,}0\ \text{cm}}{2\pi}=\dfrac{25{,}0}{2\pi}\ \text{cm} \end{align}\)
Tilavuus:
\(\begin{align} V_1&=\dfrac{4}{3}\pi r_{1}^{3} \end{align}\)
Määritetään kuorittujen appelsiinien säde ja tilavuus.
Säde:
\(\begin{align} r_2&=\dfrac{25{,}0}{2\pi}\ \text{cm}-0{,}6\ \text{cm}\\ \end{align}\)
Tilavuus:
\(\begin{align} V_2&=\dfrac{4}{3}\pi r_{2}^{3}\\ \end{align}\)
Määritetään, kuinka suuri osuus appelsiinin tilavuudesta on kuorta.
\(\begin{align} \dfrac{V_1-V_2}{V_1}&=\dfrac{\frac{4}{3}\pi r_{1}^{3}-\frac{4}{3}\pi r_{2}^{3}}{\frac{4}{3}\pi r_{1}^{3}}\\ &=\dfrac{\cancel{\frac{4}{3}\pi} \left(r_{1}^{3}-r_{2}^{3}\right)}{\cancel{\frac{4}{3}\pi} r_{1}^{3}}\\ &=1-\dfrac{r_{2}^{3}}{r_{1}^{3}}\\ &=1-\dfrac{\left(\frac{25{,}0}{2\pi}\ \text{cm}-0{,}6\ \text{cm}\right)^{3}}{\left(\frac{25{,}0}{2\pi}\ \text{cm}\right)^{3}}\\ &=0{,}38759\ldots\approx0{,}388=38{,}8\ \% \end{align}\)
Vastaus: Kuoren osuus appelsiinin tilavuudesta on noin 38,8 %.
Selvitetään kuorimistyön osuus hinnasta prosentteina.
Määritetään toisiaan vastaavat massat kuorellisia ja kuorettomia appelsiineja ja verrataan niiden hintoja.
\(m_{\text{kuoreton}}=(1-0{,}38759\ldots)m_{\text{kuorellinen}}\)
Vertailuprosentti:
\(\dfrac{m_{\text{kuoreton}}\cdot9{,}50\ \text{€/kg}-m_{\text{kuorellinen}}\cdot1{,}50\ \text{€/kg}}{m_{\text{kuoreton}}\cdot9{,}50\ \text{€/kg}}\)
\(=1-\dfrac{m_{\text{kuorellinen}}\cdot1{,}50\ \text{€/kg}}{m_{\text{kuoreton}}\cdot9{,}50\ \text{€/kg}}\)
\(=1-\dfrac{\cancel{m_{\text{kuorellinen}}}\cdot1{,}50\ \text{€/kg}}{(1-0{,}38759\ldots)\cancel{m_{\text{kuorellinen}}}\cdot9{,}50\ \text{€/kg}}\)
\(=1-\dfrac{1{,}50\ \text{€/kg}}{(1-0{,}38759\ldots)\cdot9{,}50\ \text{€/kg}}\)
\(=0{,}74217\ldots\approx0{,}742=74{,}2\ \%\)
Vastaus: Kuorimistyön osuus hinnasta on noin 74,2 %.
3.3 Analyyttinen geometria
Esim. 1 (yo, m, 2/2021S)
Geometrisia pikkutehtäviä 12 p.
Valitse oikea vaihtoehto.
Paraabelit \(y=4x^{2}\) ja \(y=x^{2}-1\) (2 p.)
Pisteiden \((1,6)\) ja \((-1,-6)\) välisen janan keskinormaalin kulmakertoimelle \(k\) on voimassa (2 p.)
Ympyrän \(9x^{2}+9y^{2}=1\) säde on (2 p.)
Tasokäyrä koostuu kaikista niistä pisteistä, jotka ovat yhtä kaukana yhdestä kiinteästä pisteestä ja yhdestä kiinteästä suorasta. Tämä tasokäyrä on (2 p.)
Kuinka monta ratkaisua on yhtälöllä \(\cos(3x)=0{,}5\) välillä \(0\lt x\lt\pi\)? (2 p.)
Ympyrälle \((x-1)^{2}+(y-1)^{2}=4\) on piirretty tangentti, joka kulkee pisteen \((0,-4)\) kautta.
Tangentti (2 p.)
Esim. 2 (yo, m, 7.4/2025S)
Geometrian laskutehtäviä 12 p.
Anna tässä tehtävässä pelkkä vastaus ilman perusteluja. Vastauslaatikkoon voi kirjoittaa vain yhden kokonaisluvun.
Laske kussakin osatehtävässä tuntemattoman likiarvo kokonaisluvuksi pyöristettynä.
Kolmion kärjet ovat pisteissä \((12, 3)\), \((-2, 9)\) ja \((4, 20)\), ja sen pinta-ala on \(A_1\). (2 p).
\(A_1\approx\)
Kolmion kärjet ovat pisteissä \((12, 3)\), \((-2, 9)\) ja \((4, 20)\), ja sen piirin pituus on \(p\). (2 p.)
\(p\approx\)
Suoran ympyrälieriön korkeus on \(13\), säde \(4\) ja vaipan pinta-ala \(A_2\). (2 p.)
\(A_2\approx\)
Pisteen \((-20, 6)\) etäisyys suorasta \(2x+y+5=0\) on \(d\). (2 p.)
\(d\approx\)
Olkoot \(\bar{u}=\bar{i}+2\bar{j}\) ja \(\bar{v}=2\bar{i}-2\bar{j}\). Vektorien \(\bar{u}\) ja \(\bar{v}\) välinen kulma asteina on \(\alpha\). (2 p.)
\(\alpha\approx\)
Olkoot \(\bar{u}\) ja \(\bar{v}\) kuten osatehtävässä 7.5. Vektorin \(4\bar{u}-7\bar{v}\) pituus on \(L\). (2 p.)
\(L\approx\)
Esim. 3 (yo, m, 2/2022S)
Analyyttistä geometriaa 12 p.
- Määritä janan \(AB\) keskipiste, \(A=(5,5)\) ja \(B=\left(-2,\frac{3}{2}\right)\). (4 p.)
- Ratkaise yhtälö \(\left|3x+4\right|=5\). (4 p.)
- Määritä ympyrän \(x^{2}+y^{2}+2x-8=0\) keskipiste ja säde. (4 p.)
Esim. 4 (yo, m, 8/2025K)
Janojen pituudet 12 p.
Tasossa on pisteet \(A=(-6,-1)\), \(B=(-1,11)\) ja \(C=(8,-1)\). Valitaan piste \(X\) janalta \(AB\), piste \(Y\) janalta \(BC\) ja piste \(Z\) janalta \(AC\) niin, että \(\left|AX\right|=\left|AZ\right|=a\), \(\left|BX\right|=\left|BY\right|=b\) ja \(\left|CZ\right|=\left|CY\right|=c\).
Muodosta yhtälöryhmä luvuille \(a\), \(b\) ja \(c\), ja ratkaise se.
3.4 Vektorit tasossa
Esim. 1 (yo, m, 2/2020K)
Vektorilaskuja 12 p.
Tutkitaan vektoreita \(\bar{a}=7\bar{i}+2\bar{j}\) ja \(\bar{b}=-3\bar{i}+5\bar{j}\).
Älä perustele tämän tehtävän vastauksia. Tässä tehtävässä ei voi käyttää kuvakaappauksia eikä kaavaeditoria, \(\bar{i}\) ja \(\bar{j}\) kirjoitetaan muodossa i ja j. Kunkin vastauksen enimmäispituus on 30 merkkiä.
Laske \(\bar{a}+\bar{b}\). (2 p.)
\(\bar{a}+\bar{b}=\)Laske \(\bar{b}-2\bar{a}\). (2 p.)
\(\bar{b}-2\bar{a}=\)Laske \(\left|\bar{b}\right|^{2}\). (2 p.)
\(\left|\bar{b}\right|^{2}=\)Laske vektorin \(\bar{a}+\bar{b}\) pituus kahden desimaalin tarkkuudella. (2 p.)
Vastaus:Laske \(\bar{a}\cdot\bar{b}\). (2 p.)
\(\bar{a}\cdot\bar{b}=\)Laske vektorien \(\bar{a}\) ja \(\bar{b}\) välinen kulma asteen tarkkuudella. (2 p.)
Vastaus: astetta.
- 4i+7j
- -17i+j
- 34
- 8,06
- -11
- 105
Esim. 2 (yo, m, 7.5-6/2025S)
Geometrian laskutehtäviä 12 p.
Anna tässä tehtävässä pelkkä vastaus ilman perusteluja. Vastauslaatikkoon voi kirjoittaa vain yhden kokonaisluvun.
Laske kussakin osatehtävässä tuntemattoman likiarvo kokonaisluvuksi pyöristettynä.
Kolmion kärjet ovat pisteissä \((12, 3)\), \((-2, 9)\) ja \((4, 20)\), ja sen pinta-ala on \(A_1\). (2 p).
\(A_1\approx\)
Kolmion kärjet ovat pisteissä \((12, 3)\), \((-2, 9)\) ja \((4, 20)\), ja sen piirin pituus on \(p\). (2 p.)
\(p\approx\)
Suoran ympyrälieriön korkeus on \(13\), säde \(4\) ja vaipan pinta-ala \(A_2\). (2 p.)
\(A_2\approx\)
Pisteen \((-20, 6)\) etäisyys suorasta \(2x+y+5=0\) on \(d\). (2 p.)
\(d\approx\)
Olkoot \(\bar{u}=\bar{i}+2\bar{j}\) ja \(\bar{v}=2\bar{i}-2\bar{j}\). Vektorien \(\bar{u}\) ja \(\bar{v}\) välinen kulma asteina on \(\alpha\). (2 p.)
\(\alpha\approx\)
Olkoot \(\bar{u}\) ja \(\bar{v}\) kuten osatehtävässä 7.5. Vektorin \(4\bar{u}-7\bar{v}\) pituus on \(L\). (2 p.)
\(L\approx\)
- \(95\)
- \(47\)
- \(327\)
- \(13\)
- \(108\)
- \(24\)
Esim. 3 (yo, m, 2/2021K)
Vektoreita ja analyyttista geometriaa 12 p.
Olkoon \(\bar{u}=5\bar{i}+12\bar{j}\).
Määritä vektorin \(\bar{u}\) pituus. (3 p).
Määritä vektorin \(\bar{u}\) kanssa vastakkaissuuntainen vektori, jonka pituus on 5. (3 p.)
Suora \(L\) kulkee pisteiden \(A=(4,4)\) ja \(B=(-1,-8)\) kautta. Ovatko suora \(L\) ja vektori \(bar{u}\) yhdensuuntaisia? (3 p.)
Määritä suoran \(L\) yhtälö muodossa \(y=kx+b\). (3 p.)
4 FUNKTIOT JA YHTÄLÖ 2
4.1 Trigonometriset funktiot
Esim. 1 (yo, m, 1.3/2025K)
Perustehtäviä 12 p.
Anna tässä tehtävässä pelkkä vastaus ilman perusteluja. Vastauskenttään voi kirjoittaa vain yhden kokonaisluvun.
Ratkaise yhtälö \(\sin \frac{x}{2}=\frac{1}{2}\), kun \(0^{\circ}\lt x\lt90^{\circ}\). (2 p.)
\(x=\) astetta
- \(60\)
Esim. 2 (yo, m, 4/2025S)
Trigonometrinen yhtälö 12 p.
Ratkaise yhtälö \(1-(\cos x)^{2}=(\sin 2x)^{2}\), kun \(x\in\left[-\pi,\pi\right]\).
Esim. 3 (yo, m, 11/2020S)
Trigonometriset yhtälöt 12 p.
Seuraavia yhtälöitä tarkastellaan vain muuttujan arvoilla \(x\in\left[0,\pi\right]\).
Ratkaise yhtälö \(\cos x+\sin x=0\). (2 p).
Osoita, että yhtälöllä \((\cos x)^{2}+\cos x\sin x+(\sin x)^{2}=0\) ei ole ratkaisua. (4 p.)
Selvitä perustellen yhtälön \(\sum_{k=0}^{n}(\cos x)^{n-k}(\sin x)^{k}=0\) kaikki ratkaisut, kun \(n=3, 4, 5,\ldots\) (6 p.)
Esim. 4 (yo, m, 9/2024S)
Jaksollisuus 12 p.
Funktio \(f:\mathbb{R}\to\mathbb{R}\) on jaksollinen, jos on olemassa sellainen \(L\gt0\), että sen kuvaaja pysyy samana, kun sitä siirrtään \(L\) yksikköä vaakasuorassa suunnassa. Tämä ominaisuus voidaan esittää myös ehdolla \(f(x+L)=f(x)\) kaikilla \(x\in\mathbb{R}\). Pienin tällainen luku \(L\) on funktion perusjakso.
Piirrä jokaisessa osatehtävässä funktion kuvaaja omaan koordinaatistoonsa. Anna vastauksena funktion perusjakso sekä kuvaaja, johon on merkitty perusjakson mittainen osa \(x\)-akselia.
\(f(x)=\sin(2\pi x)\) (4 p.)
\(g(x)=\left|\sin(\pi x)+\sin(2\pi x)\right|\) (4 p.)
Anna esimerkki jaksollisesta funktiosta \(h:\mathbb{R}\to\mathbb{R}\), jonka perusjakso on 4. (4 p.)
4.2 Eksponenttifunktiot
Esim. 1
Ratkaise yhtälö \(4^{x}=64\).
Esim. 2 (yo, m, 3.1/2024S)
Yhtälöt 12 p.
Ratkaise muuttujien \(x\) ja \(y\) tarkat arvot seuraavista yhtälöistä.
Yhtälö \(4\cdot8^{x}=\sqrt{2}\). (4 p.)
Yhtälö \(\sin(6y-\frac{\pi}{2})=\frac{1}{2}\), kun \(y\in\left[0,\frac{\pi}{2}\right]\). (8 p.)
Esim. 3 (yo, m, 13/2021S)
Eksponenttiyhtälö 12 p.
Tutki yhtälön \(e^{ax}=\ln x\) positiivisten ratkaisujen lukumäärää kaikilla parametrin \(a\gt0\) eri arvoilla.
4.3 Logaritmifunktiot
Esim. 1
Ratkaise yhtälö \(\log_{4}(3x+1)=2\).
Esim. 2 (yo, m, 1.5/2025S)
Yks, kaks, kolme, neljä 12 p.
Valitse oikea vaihtoehto. Vastauksia ei tarvitse perustella.
Sievennä \(\log_{a}1+\log_{a}2^{3}+\log_{a}4\), kun \(a\gt0\). (2 p.)
Esim. 3 (yo, m, 3/2020S)
Logistinen regressio 12 p.
Logistinen regressio on malli, jota käytetään esimerkiksi tutkittaessa riskiä sairastua erilaisiin sairauksiin, kuten esimerkiksi sepelvaltimotautiin.
Logistinen regressio \(y\) riippuu muuttujasta \(x\) yhtälön $$\ln\dfrac{y}{1-y}=a+bx$$ mukaisesti. Vakiot \(a\) ja \(b\) valitaan mallinnettavan ilmiön mukaan.
Ratkaise \(y\) logistisen regression yhtälöstä. (6 p.)
Olkoon \(a=2\) ja \(b=-1\). Millä muuttujan \(x\) arvolla \(y\) saa arvon \(0{,}5\)? (6 p.)
5 ANALYYSI
5.1 Raja-arvo
Raja-arvon määritelmä
Funktiolla \(f\) on kohdassa \(a\) raja-arvo \(b\), kun
$$\lim_{x\to a} f(x)=b \quad \Leftrightarrow \quad \lim_{x\to a-} f(x)=\lim_{x\to a+} f(x)=b.$$5.2 Jatkuvuus
Määritelmä
Funktio \(f\) on jatkuva kohdassa \(x=a\), jos funktion \(f\) raja-arvo on sama kuin funktion \(f\) arvo kohdassa \(x=a\) eli $$\lim_{x\to a}f(x)=f(a).$$
Siis funktion \(f\) jatkuvuus kohdassa \(x=a\) edellyttää, että
funktio \(f\) on määritelty kohdassa \(x=a\),
funktiolla \(f\) on raja-arvo kohdassa \(x=a\) ja
funktion \(f\) raja-arvo ja funktion \(f\) arvo kohdassa \(x=a\) ovat yhtä suuret.
Huom.
Jos funktiota ei ole määritelty jossakin kohdassa, ei tässä kohdassa ole mielekästä puhua jatkuvuudesta laisinkaan.
Jos funktio on määritelty, mutta ei jatkuva jossakin kohdassa, voimme sanoa, että funktio on epäjatkuva tässä kohdassa.
Funktion jatkuvuus välillä
Toispuolisesti jatkuva funktio
Funktio \(f\) on kohdassa \(x=a\)
- vasemmalta jatkuva, jos funktion \(f\) vasemmanpuolinen raja-arvo on yhtä suuri kuin funktion arvo kohdassa \(x=a\), $$\lim_{x\to a-}f(x)=f(a)$$
- oikealta jatkuva, jos funktion \(f\) oikeanpuolinen raja-arvo on yhtä suuri kuin funktion arvo kohdassa \(x=a\), $$\lim_{x\to a+}f(x)=f(a)$$
- toispuolisesti jatkuva, jos se on vasemmanpuolisesti jatkuva tai oikeanpuolisesti jatkuva.
Sanomme lisäksi, että funktio \(f\) on
kaikkialla jatkuva, jos se on jatkuva koko reaalilukujoukossa,
jatkuva, jos se on jatkuva koko määrittelyjoukossaan.
Huom.
Alkeisfunktiot ja niistä peruslaskutoimituksilla, itseisarvolla ja yhdistämällä muodostetut funktiot ovat määrittelyjoukossaan jatkuvia.
5.3 Derivaatta
Derivaatta
Funktion \(f\) derivaatta kohdassa \(a\) on $$f'(a)=\lim_{x\to h}\frac{f(a+h)-f(a)}{h}=\lim_{x\to a}\frac{f(x)-f(a)}{x-a},$$ jos tällainen raja-arvo on olemassa.
Sanomme, että funktio \(f\) on
derivoituva kohdassa \(a\), jos funktiolla on derivaatta kohdassa \(a\),
kaikkialla derivoituva, jos se on derivoituva koko reaalilukujoukossa,
derivoituva, jos se on derivoituva koko määrittelyjoukossaan.
5.4 Derivointi
Esim. 1 (yo, m, A2/2024S)
Derivaattoja 12 p.
Valitse oikea vaihtoehto. Vastauksia ei tarvitse perustella.
Määritä luvun \(p'(1)\) tarkka arvo, kun \(p(x)=-2x^5+x^4-2\). (3 p.)
\(p'(1)=\ \)
Määritä derivaatta \(f'(x)\), kun \(f(x)=xe^x\). (3 p.)
\(f'(x)=\ \)
Määritä luvun \(g'(-1)\) tarkka arvo, kun \(g(x)=\ln (2x+3)\). (3 p.)
\(g'(-1)=\ \)
Määritä derivaatta \(h'(x)\), kun \(h(x)=\sin x+\cos(3x)\). (3 p.)
\(h'(x)=\ \)
Esim. 2 (yo, m, A4/2020S)
Käyrän tangentteja 12 p.
Käyrällä $$y=x^3-5x^2+2x+8=(x-4)(x-2)(x+1)$$ on kaksi tangenttia, jotka kulkevat pisteen \((2,0)\) kautta. Määritä niiden yhtälöt.
Vihje: Käyrän tangentti pisteessä \((2,0)\) antaa toisen kysytyistä yhtälöistä.
5.5 Funktion kulku
Esim. 1 (yo, m, A3/2023S)
Minimointi 12 p.
Määritä funktion \(f(x)=x^2+\dfrac{16}{x^2}\) pienin arvo, kun \(x\gt0\).
Esim. 2 (yo, m, A5/2025K)
Suurin arvo 12 p.
Määritä funktion \(f(x)=x^{2025}e^{-x}\) suurin arvo, kun \(x\ge0\).
5.6 Integrointi
Esim. 1 (yo, m, A3/2021s)
Integraaleja 12 p.
Jokaisesta osatehtävästä voi saada 4 pistettä.
Laske $$\displaystyle{\int}(x^2+1)\,\text{d}x.$$
Laske $$\displaystyle{\int_{0}^{\frac{\pi}{2}}}\cos(2x)\,\text{d}x.$$
Laske $$\displaystyle{\int_{-1}^{1}}\left|x\right|^{3}\,\text{d}x.$$
5.7 Pinta-alaintegraali
Esim. 1 (yo, m, A3/2022S)
Integraalilaskuja 12 p.
Määritä \(\displaystyle{\int}\left(-2x^2+6x-4\right)\text{d}x\). (4 p.)
Määritä käyrien \(y=(x-1)(3-x)\) ja \(y=(x-1)^2\) väliin jäävän rajoitetun alueen pinta-ala. (8 p.)
Esim. 2 (yo, m, A3/2020K)
Pinta-alan ääriarvo 12 p.
Laske integraali \(\displaystyle{\int_{0}^{2}}\sin\left(\frac{\pi}{2}x\right)\text{d}x\). (3 p.)
Funktion \(f(x)=\sin\left(\frac{\pi}{2}x\right)\) kuvaajan ja \(x\)-akselin rajoittamasta alueesta leikataan pystysuora kaistale suorilla \(x=t\) ja \(x=t+\frac{1}{2}\). Millä parametrin arvolla \(0\le t\le\frac{3}{2}\) kaistaleen pinta-ala on suurin mahdollinen? (9 p.)
Esim. 3 (yo, m, A4/2022K)
Polynomit 12 p.
Polynomien \(f(x)=(x-2)(x+2)(x-1)\) ja \(g(x)=-2(x-2)(x+2)(x+1)\) kuvaajat leikkaavat toisensa kolmessa pisteessä \((2,0)\), \((-2,0)\) ja \((x_0,y_0)\), missä \(-2\lt x_0\lt0\).
Määritä leikkauspiste \((x_0,y_0)\). (4 p.)
Laske polynomien kuvaajien väliin jäävän alueen pinta-ala välillä \(\left[0,2\right]\). (8 p.)
Esim. 4 (yo, m, B9/2023S)
Taidemuseon aaltoileva aita 12 p.
Taidemuseon aita halutaan maalata ja sen pinta-alaa mallinnetaan integraalilla $$\int_{0}^{4}\left(\dfrac{\cos(10x+x^2)}{2}+1\right)\,\text{d}x.$$
Arvioi integraalia puolisuunnikassäännön avulla käyttäen 10:tä ja 100:aa jakoväliä. Laske näiden arvioiden suhteelliset virheet, kun integraalin arvo viiden desimaalin tarkkuudella on 3,98636.
5.8 Tilavuusintegraali
Esim. 1 (yo, m, B6/2023K)
Raketin nokkakartio 12 p.
Erään raketin kärki, eli niin sanottu nokkakartio, saadaan, kun alaspäin aukeava paraabeli pyörähtää symmetria-akselinsa ympäri. Kärjen korkeus on 4,5 metriä, ja sen halkaisija pohjan tasolla on 3,3 metriä. Määritä kärjen tilavuus.
6 TILASTOT, TODENNÄKÖISYYS, TALOUS
6.1 Tilastot
Esim. 1 (yo, m, A5/2025S)
Tilastollisia tunnuslukuja 12 p.
Lukujen \(x_{1}, \ldots ,x_{n}\) keskiarvo on \(a\) ja \(b\gt a\). Osoita, että lukujen \(x_{1}, \ldots ,x_{n},b\) keskiarvo on suurempi kuin \(a\). (6 p.)
Anna esimerkki seuraavat ehdot toteuttavista luvuista tai osoita, että sellaisia ei ole olemassa: lukujen moodi on on \(1\), keskiarvo \(10\) ja mediaani \(100\). (6 p.)
6.2 Todennäköisyys
Esim. 1 (yo, m, B7/2020K)
Yatzy 12 p.
Yatzy-noppapelissä pelaaja heittää viittä noppaa. Tutkitaan tarkemmin heittoja, joiden tuloksena saadaan täyskäsi tai neliluku yhdellä viiden nopan heitolla. Täyskädellä tarkoitetaan tulosta, jossa yksi silmäluku esiintyy kolme kertaa ja joku toinen silmäluku kaksi kertaa. Neliluvussa esiintyy neljä samaa silmäluku ja yksi muu silmäluku.
Määritä todennäköisyys sille, että saadaan täyskäsi, jossa esiintyy kolme kuutosta ja kaksi viitosta. (3 p.)
Määritä todennäköisyys sille, että saadaan täyskäsi. (6 p.)
Määritä todennäköisyys sille, että saadaan neliluku. (3 p.)
Esim. 2 (yo, m, B7/2020S)
Koripalloilijan vapaaheitot 12 p.
Pitkäaikaisten tilastojen perusteella erään koripalloilijan todennäköisyys heittää pallo vapaaheitolla koriin on \(p\) \((0\le p\le1)\). Rautahermoisena pelaajana hänen heittojensa onnistumistodennäköisyydet ovat riippumattomia aikaisempien heittojen tuloksista ja pelitilanteesta.
Eräässä ottelussa kyseinen pelaaja saa kaksi vapaaheittoa, jotka on heitettävä peräkkäin. Merkitään
\(P(0)=\) todennäköisyys sille, että pelaaja ei saa yhtään heittoa koriin
\(P(1)=\) todennäköisyys sille, että pelaaja saa täsmälleen yhden heiton koriin
\(P(2)=\) todennäköisyys sille, että pelaaja saa kaksi heittoa koriin.
Laske \(P(2)\), kun \(p=0{,}82\). (3 p.)
Määritä \(P(2)\), \(P(1)\) ja \(P(0)\) todennäköisyyden \(p\) avulla lausuttuina. (6 p.)
Millä todennäköisyyden \(p\) arvoilla on \(P(1)=P(2)\)? (3 p.)
6.3 Talousmatematiikka
Esim. 1 (yo, m, A1.1-3/2021K)
Lukujonoja ja funktioita 12 p.
Oikea vastaus 2 p., väärä vastaus 0 p., ei vastausta 0 p.
Lukujono \((1,2,4,7, \ldots)\) (2 p.)
Lukujono \((32,16,8,4, \ldots)\) (2 p.)
Lukujono \((7,9,11,13, \ldots)\) (2 p.)
Esim. 2 (yo, m, A1.2-3/2021S)
Sopivia lukuja 12 p.
Valitse oikea vaihtoehto.
Mikä on lausekkeen \(1-3x\) arvo,kun \(x=2\)? (3 p.)
Jonon \((a_{n})\) yleinen termi on muotoa \(a_{n}=3\cdot2^{n}\), \(n\in \mathbb{N}\). Mikä on termi \(a_{3}\)? (3 p.)
Jono \((b_{n})\) toteuttaa ehdot \(b_{6}=6\) ja \(b_{n+1}=b_{n}+4\), \(n\in\mathbb{N}\). Mikä on termi \(b_{4}\)? (3 p.)
Polynomi \((x^2+5x+1)(x+3)\) kerrotaan auki, jolloin muodostuu kolmannen asteen polynomi. Mikä on sen toisen asteen termin kerroin? (3 p.)
7 VALINNAISET
7.1 Vektorit avaruudessa
Esim. 1 (yo, m, B13/2025K)
Vektorien ristitulo 12 p.
Vektorien \(\bar{a}=a_{x}\bar{i}+a_{y}\bar{j}+a_{z}\bar{k}\) ja \(\bar{b}=b_{x}\bar{i}+b_{y}\bar{j}+b_{z}\bar{k}\) ristitulo määritellään lausekkeella $$\bar{a}\times\bar{b}=(a_{y}b_{z}-a_{z}b_{y})\bar{i}+(a_{z}b_{x}-a_{x}b_{z})\bar{j}+(a_{x}b_{y}-a_{y}b_{x})\bar{k}.$$Todista tätä lauseketta käyttäen seuraavat ristitulovektorin tunnetut ominaisuudet:
Se on kohtisuorassa vektoria \(\bar{a}\) vastaan. (3 p.)
Sen pituus on sama kuin vektorien \(\bar{a}\) ja \(\bar{b}\) virittämän suunnikkaan ala. (9 p.)
7.2 Ääriarvosovelluksia
Esim. 1 (yo, m, B10/2022K)
Veistos 12 p.
10.A Kuva: Funktion kuvaaja

Lähde: YTL.
Puistossa sijaitseva veistos on rakennettu käyttäen rautatankoja geometristen muotojen särminä kuvan 10.A mukaisesti. Veistoksen yläosa on pyramidi ja alaosa on suorakulmainen särmiö, jonka pohja on neliön muotoinen. Tiedekeskuksen pihalle on tarkoitus rakentaa vaakasuoralle alustalle samanmallinen veistos, jossa särmiön kehikkoon, jossa särmiön kehikkoon kuuluu myös pohjaneliön sivutangot (kuvassa pohjaneliö ei ole näkyvissä). Uuden rakennelman pitää toteuttaa seuraavat ehdot: rakennelman sisätilavuus on 21 kuutiometriä ja yläosan (pyramidin) korkeus on puolet alaosan korkeudesta. Mikä on tähän rakennelmaan tarvittavan rautatangon pienin mahdollinen kokonaispituus \(L\)?
Tehtävässä oletetaan, että rautatangon koko pituus \(L\) voidaan käyttää rakennelmaan. Liitoksiin käytettävää materiaalia ei tarvitse ottaa huomioon. Anna vastaus metreinä kahden merkitsevän numeron tarkkuudella.
7.3 Osittaisderivaatta
Esim. 1 (yo, m, B10/2021S)
Osittaisderivaatta 12 p.
10.A Kuva: Funktion kuvaaja
Lähde: YTL.
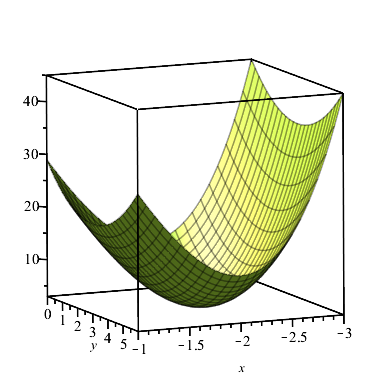
Tarkastellaan kahden muuttujan funktiota $$f(x,y)=x^{4}+32x+y^{2}-6y+60.$$
Laske funktion \(f\) osittaisderivaatat \(f_x\) ja \(f_y\). (4 p.)
Oletetaan tunnetuksi, että tämän funktion \(f\) pienin arvo saadaan siinä pisteessä, jossa yhtälöpari $$\begin{cases}f_x=0\\f_y=0\end{cases}$$ toteutuu (ks. kuva 10.A). Määritä funktion \(f\) pienin arvo tätä tietoa käyttämällä. (8 p.)
Huomautus: Osittaisderivaatalle \(f_x\) käytetään myös merkintöjä \(f_{x}', D_{x}f, D_{1}f, \dfrac{\partial f}{\partial x}\) ja \(\partial_{1}f\); vastaavalla tavalla osittaisderivaatalle \(f_y\).
7.4 Lukuteoria
Esim. 1 (yo, m, A6/2025K)
Eukleideen algoritmi 12 p.
Määritä Eukleideen algoritmilla lukujen 5322 ja 342 suurin yhteinen tekijä.
Eukleideen algoritmi perustuu tietoon, että jaettavalla, jakajalla ja jakojäännöksellä on sama suurin yhteinen tekijä.
Eukleideen algoritmin mukaan tulee muodostaa jakolaskun 5322:342 jakoyhtälö. Jos jää positiivinen jakojäännös, jatketaan muodostamalla edellisen jakolaskun jakajan ja jakojäännöksen jakoyhtälö. Näin jatketaan kunnes jakojäännökseksi saadaan 0. Viimeiseksi jäänyt positiivinen jakojäännös on lukujen suurin yhteinen tekijä.
\(5322:342=15\) jää
\(5322-15\cdot342=192\)
Jakoyhtälö: \(5322=342\cdot15+192\)
\(342:192=1\) jää
\(342-1\cdot192=150\)
Jakoyhtälö: \(342=192\cdot1+140\)
\(192:150=1\) jää
\(192-1\cdot150=42\)
Jakoyhtälö: \(192=150\cdot1+42\)
\(150:42=3\) jää
\(150-3\cdot42=24\)
Jakoyhtälö: \(150=42\cdot3+24\)
\(42:24=1\) jää
\(42-1\cdot24=18\)
Jakoyhtälö: \(42=24\cdot1+18\)
\(24:18=1\) jää
\(24-1\cdot18=6\)
Jakoyhtälö: \(24=18\cdot1+6\)
\(18:6=3\) jää \(0\)
Jakoyhtälö: \(18=6\cdot3+0\)
Vastaus: Lukujen 5322 ja 342 suurin yhteinen tekijä on 6.
7.5 Algoritmit
Esim. 1 (yo, m, B10/2025S)
Eukleideen algoritmi 12 p.
Määritä Eukleideen algoritmilla lukujen 121 110 987 654 321 ja 123 456 789 101 112 suurin yhteinen tekijä. Voit käyttää ohjelmistoa, kunhan algoritmin välivaiheet näkyvät ratkaisussa.
Eukleideen algoritmi perustuu tietoon, että jaettavalla, jakajalla ja jakojäännöksellä on sama suurin yhteinen tekijä.
Eukleideen algoritmin mukaan tulee muodostaa jakolaskun
Ohjelmoidaan while-silmukka, joka laskee jakojäännöksiä, kunnes arvoksi saadaan 0.
Python-koodi, joka tulostaa suurimman yhteisen tekijän
a=123456789101112
b=121110987654321
while(b>0):
c=a-(a//b)*b
a=b
b=c
print(a)
Python-koodi, joka tulostaa jakoyhtälöt ja suurimman yhteisen tekijän:
a=123456789101112
b=121110987654321
while(b>0):
c=a%b
q=a//b
print(f'{a} = {q} * {b} + {c}')
a=b
b=c
print(f'suurin yhteinen tekijä on {a}')
Vastaus: Suurin yhteinen tekijä on 3.
7.6 Analyysi
Esim. 1 (yo, m, B9/2020K)
Käänteisfunktion derivaatta 12 p.
Anna esimerkki funktiosta \(f\), jonka käänteisfunktion derivaatalle pätee \((f^{-1})'(2) =\frac{1}{2}\). Muista perustella, miksi esimerkilläsi on vaadittu ominaisuus.
Esimerkiksi käy \(f(x)=2x\).
Perustelu:
Funktio \(f(x)=2x\) on aidosti monotoninen, joten se on kääntyvä, ja \(f'(x)=2\).
Koska
\(({{f}^{-1}})'(y_0)=\dfrac{1}{f'(x_0)}\),
niin saadaan
\((f^{-1})'(2)=\dfrac{1}{f'((f^{-1})'(2))}=\dfrac{1}{2}\)
kaikilla \(x\in \mathbb{R}\).
7.7 Jatkuvat jakaumat
Esim. 1 (yo, m, B10/2025K)
Eksponenttijakauma 12 p.
Eksponenttijakaumaa voi käyttää esimerkiksi hiukkassäteilyn tai asiakasvirtojen mallintamiseen. Jakauman tiheysfunktio (vakiolla \(\lambda\gt0\)) on $$f_{\lambda}(x)=\begin{cases}\lambda e^{-\lambda x},&\text{kun}\ x\ge0,\\0&\text{muuten}.\end{cases}$$ Satunnaismuuttuja \(X\) noudattaa tätä jakaumaa. Määritä todennäköisyys \(P(X\ge7)\), joka riippuu