Tilastot ja todennäköisyys (MAB5)
Laajuus
2 op
Yleiset tavoitteet (LOPS 2021)
Moduulin tavoitteena on, että opiskelija
- harjaantuu käsittelemään, havainnollistamaan ja tulkitsemaan tilastollisia aineistoja
- perehtyy todennäköisyyslaskennan perusteisiin ja sitä havainnollistaviin malleihin
- osaa käyttää ohjelmistoja digitaalisessa muodossa olevan datan hakemisessa, käsittelyssä ja tutkimisessa sekä havaintoaineiston tunnuslukujen määrittämisessä ja todennäköisyyslaskennassa.
Keskeiset sisällöt (LOPS 2021)
- tilastoaineiston havainnollistaminen ja tunnuslukujen määrittäminen
- regression ja korrelaation käsitteet
- havainto ja poikkeava havainto
- ennusteiden tekeminen
- todennäköisyyden käsite
- yhteen- ja kertolaskusääntö
- kombinaatiot ja tuloperiaate
- todennäköisyyslaskennan malleja
Aikataulu
Suoritus
- osallistuminen
- tehtävien tekeminen
- monivalintatehtävien tekeminen
- loppukoe
Arviointi
- säännöllinen, aktiivinen ja vastuullinen osallistuminen +1 p
- tehtävien asianmukainen ja jatkuva tekeminen +1 p
- oppikirjan jaksojen monivalintatehtävistä 1 p kustakin 80 % oikein tehdystä ja ajoissa palautetusta monivalintatehtäväkokonaisuudesta, max. 6 p
- loppukokeesta max. 54 p
- yhteensä max. 60 p (teoreettisesti max. 62 p)
- 30 % arviointi
| Pisteet | Arvosana | Muuta |
|---|---|---|
| 0 - 9 | i \(\to\) K | Pakko täydentää. |
| 10 - 17 | 4 | Oikeus täydentää. |
| 18 - 25 | 5 | |
| 26 - 33 | 6 | |
| 34 - 41 | 7 | |
| 42 - 49 | 8 | |
| 50 - 57 | 9 | |
| 58 - 60 | 10 |
Keskeyttäminen
Opettaja keskeyttää opiskelijan opintojakson, jos
- opiskelija niin pyytää
- opiskelija ei ole läsnä opintojakson kahdella ensimmäisellä opetuskerralla ja opiskelija ei ole yhteydessä opettajaan eikä opettaja saa yhteyttä opiskelijaan.
Opettaja voi keskeyttää opiskelijan opintojakson, jos opiskelijalla on viisi poissaoloa. Tällaiset tilanteet opettaja käy läpi tapauskohtaisesti ja on ennen lopullista keskeytystä yhteydessä opiskelijaan.
Keskeyttämisestä opettaja merkitsee opintojaksosta opiskelijalle K-merkinnän Wilmaan ja poistaa opiskelijan sen jälkeen Wilman ryhmästä. Opettaja lähettää keskeyttämisestä viestin opiskelijalle, alaikäisen opiskelijan huoltajalle, ryhmänohjaajalle ja opolle.
1 TILASTO
1.1 Käsitteitä
Tilasto on valikoitu ja järjestetty kokoelma tietoa, joka perustuu havaintoaineistoon.
Havaintoaineisto on tilastollisella tutkimuksella kerättyä usein taulukkomuotoista tietoa jostain mielenkiinnon kohteesta.
- Jos tutkitaan kaikki mielenkiinnon kohteena olevan joukon jäsenet eli niin kutsuttu perusjoukko, kyseessä on kokonaistutkimus.
- Jos koko perusjoukon tutkiminen on liian vaativaa, voidaan perusjoukosta kerätä tarpeeksi edustava otos ja yleistää otoksesta saadut tulokset perusjoukkoon. Tällaista tutkimusta kutsutaan otantatutkimukseksi.
Tilastollisessa tutkimuksessa mitataan muuttujan eli mielenkiinnon kohteen jonkin ominaisuuden (esim. silmien väri, pituus, paino, puoluekanta) saamia vaihtelevia arvoja eli havaintoarvoja.
Arvojen vaihtelusta muodostuu muuttujan jakauma. Jakauma ilmaisee muuttujan saamien eri arvojen yleisyyden.
- Absoluuttinen jakauma sisältää havaintoarvot ja niiden esiintymiskertojen lukumäärät eli frekvenssit, \(f\).
- Suhteellinen jakauma sisältää havaintoarvot ja niiden esiintymiskertojen suhteelliset osuudet prosentteina eli suhteelliset frekvenssit, \(f\ \%\).
Tilastotietoa voidaan havainnollistaa graafisesti erilaisina kuvaajina eli diagrammeina. Tavallisimpia kuvaajatyyppejä ovat:
- Pylväs- ja palkkikuvaajat (diskreetit muuttujat ja luokitellut aineistot)
- Ympyräkuvaajat eli sektoridiagrammit (suhteellinen jakauma)
- Viivakuvaaja (jatkuva jakauma, esim. ajallinen muutos)
Esim. 1
Piirrä Libre Office Calc -taulukkolaskentaohjelmalla pyydetyt kuvaajat annetusta aineistosta.
a) Pylväskuvaaja
Taulukossa on eräiden EU-maiden väkilukuja vuonna 2004. Piirrä tilastosta pylväsdiagrammi. Käytä mittakaavaa, jossa 1 ruutu vastaa 10 miljoonaa asukasta.
| Maa | Väkiluku (milj.) |
|---|---|
| Saksa | 82,4 |
| Ranska | 60,4 |
| Puola | 38,6 |
| Hollanti | 16,3 |
| Ruotsi | 9 |
| Suomi | 5,2 |
| Viro | 1,3 |
b) Viivakuvaaja
Taulukossa on erään tuotteen hinnan kehitys. Piirrä tiedoista viivadiagrammi.
| Vuosi | 2001 | 2002 | 2003 | 2004 | 2005 |
|---|---|---|---|---|---|
| Hinta (€) | 5,1 | 5,4 | 5,6 | 5,7 | 5,2 |
c) Ympyräkuvaaja
Taulukko esittää televisio-ohjelmien vastaanottotapaa suomalaisissa kotitalouksissa vuonna 2004. Esitä tilasto sektoridiagrammina.
| Televisio-ohjelmien vastaanottotapa | Osuus (%) |
|---|---|
| Tavallinen antenni | 42,00 |
| Kaapeli- tai satelliittiantenni | 52,00 |
| Ei TV:tä | 6,00 |
d) Yhdistetty viiva- ja pylväskuvaaja
Suomen kuukausittainen keskilämpötila ja sademäärän keskiarvo jaksolla 1991-2020. (Lähde: Ilmatieteenlaitos.)
| Kuukausi | Lämpötila (°C) | Sademäärä (mm) |
|---|---|---|
| 1 | -8,3 | 43 |
| 2 | -8,5 | 35 |
| 3 | -4,4 | 33 |
| 4 | 1,4 | 31 |
| 5 | 7,7 | 43 |
| 6 | 13,0 | 62 |
| 7 | 16,0 | 75 |
| 8 | 14,0 | 69 |
| 9 | 9,0 | 58 |
| 10 | 2,9 | 60 |
| 11 | -2,1 | 54 |
| 12 | -5,6 | 50 |
1.2 Tilastolliset tunnusluvut
Tilastoon sisältyvää tietoa voidaan tiivistää tilastollisten tunnuslukujen avulla.
Tilastollisia tunnuslukuja ovat muun muassa
- keskiluvut ja
- hajontaluvut.
Keskiluvut
Keskiluvut kuvaavat jakauman keskikohtaa. Keskilukuja ovat muun muassa
- moodi (Mo) eli tyyppiarvo,
- mediaani (Md) ja
- keskiarvo \(\bar{x}\).
Moodi
Moodi eli tyyppiarvo on tilaston eniten esiintyvä havaintoarvo (suurin frekvenssi).
Huom.
Jos suurin frekvenssi esiintyy useilla havaintoarvoilla, ne kaikki ovat tyyppiarvoja.
Mediaani
Mediaani on tilaston suuruusjärjestyksessä keskimmäinen havaintoarvo.
Huom.
- Jos havaintoarvoja on pariton määrä, niin mediaani on keskimmäinen.
- Jos havaintoarvoja on parillinen määrä ja ne ovat lukuja, niin mediaani on kahden keskimmäisen keskiarvo.
- Jos havaintoarvoja on parillinen määrä ja ne eivät ole lukuja, niin molemmat keskimmäiset ovat mediaaneja.
Keskiarvo
Keskiarvo on havaintoarvojen summa jaettuna havaintoarvojen lukumäärällä.
$$\bar{x}=\frac{x_{1}+x_{2}+\ldots+x_{n}}{n}=\frac{\sum_{i=1}^{n}x_{i}}{n},$$
missä \(x_{1}, x_{2},\ldots, x_{n}\) ovat havaintoarvoja ja \(n\) havaintoarvojen lukumäärä.
Huom.
Jos tilasto on esitetty frekvenssitaulukkona, keskiarvo voidaan laskea seuraavasti.
$$\bar{x}=\frac{f_{1}x_{1}+f_{2}x_{2}+\ldots+f_{k}x_{k}}{n}=\frac{\sum_{i=1}^{k}f_{i}x_{i}}{n}$$
| Havaintoarvo | Frekvenssi |
|---|---|
| \(x_{1}\) | \(f_{1}\) |
| \(x_{2}\) | \(f_{2}\) |
| \(\vdots\) | \(\vdots\) |
| \(x_{k}\) | \(f_{k}\) |
| Yht. | \(n\) |
Esim. 1
Määritä havaintoaineiston mediaani, moodi ja keskiarvo, jos mahdollista.
a) 8, 7, 9, 10, 9, 6, 9
b) 4, 5, 1, 3, 2, 1, 4, 2
c) kenraali, kersantti, majuri, luutnantti, kersantti
d) sininen, keltainen, sininen, punainen.
Hajontaluvut
Hajontaluvut kuvaavat, kuinka paljon havaintoarvot vaihtelevat keskiarvon ympärillä.
Hajontalukuja ovat muun muassa
- vaihteluväli,
- vaihteluvälin pituus,
- keskihajonta ja
- otoskeskihajonta.
Vaihteluväli ilmaistaan ilmoittamalla tilaston pienin ja suurin havaintoarvo.
Vaihteluvälin pituus on tilaston suurimman ja pienimmän havaintoarvon erotus.
Keskihajonta kuvaa, miten havaintoarvot ovat jakautuneet keskiarvon ympärille. Mitä lähempänä nollaa keskihajonnan arvo on, sitä lähemmäksi keskiarvoa havaintoarvot tilastossa sijoittuvat.
Perusjoukon keskihajonta, \(\sigma\), tarkoittaa koko perusjoukon keskihajontaa.
Otoskeskihajonnalla, \(s\), tarkoitetaan perusjoukosta valikoidun osajoukon eli otoksen keskihajontaa. Koska perusjoukon tutkiminen on työlästä, miltei aina on kyseessä otoskeskihajonta.
Huom.
Tässä opintojaksossa ei tarvitse erottaa keskihajontaa ja otoskeskihajontaa toisistaan.
1.3 Tunnusluvut laskinohjelmilla
GeoGebran komentoja
- havaintoarvojen lukumäärä
=Pituus() - moodi eli tyyppiarvo
=Tyyppiarvo() - mediaani
=Mediaani() - keskiarvo
=Keskiarvo() - keskihajonta
=Keskihajonta() - otoskeskihajonta
=Otoskeskihajonta() - pienin arvo
=Min() - suurin arvo
=Max()
LibreOffice Calc -ohjelman komentoja
- havaintoarvojen lukumäärä
=LASKE.A() - moodi eli tyyppiarvo
=MOODI.USEA() - mediaani
=MEDIAANI() - keskiarvo
=KESKIARVO() - keskihajonta
=KESKIHAJONTA.P() - otoskeskihajonta
=KESKIHAJONTA.S() - pienin arvo
=MIN() - suurin arvo
=MAKS()
Huom.
LibreOffice Calc -ohjelmalla kannattaa käyttää ohjattua kaavojen luonti -toimintoa. Tällöin ei tarvitse muistaa komentoja ulkoa. Lisäksi komennon =MOODI.USEA() onnistunut käyttö saattaa vaatia ohjattua kaavojen luontia.
Esim. 1
Alla olevassa aineistossa on taulukoituna erään abin kaikista pitkän matematiikan opintojaksoista saamat arvosanat. Määritä Libre Office Calc -taulukkolaskentaohjelmalla arvosanojen
a) mediaani
b) moodi
c) vaihteluväli
d) vaihteluvälin pituus
e) keskiarvo
f) keskihajonta.
| Opintojakso | Arvosana |
|---|---|
| MAY1 | 7 |
| MAA2 | 8 |
| MAA3 | 8 |
| MAA4 | 8 |
| MAA5 | 7 |
| MAA6 | 7 |
| MAA7 | 7 |
| MAA8 | 5 |
| MAA9 | 9 |
| MAA10 | 6 |
| MAA11 | 4 |
| MAA12 | 5 |
| MAA13 | 7 |
2 JAKAUMA
2.1 Diskreetti muuttuja
Tilastollinen muuttuja on diskreetti, jos se saa erillisiä arvoja, esimerkiksi kokonaislukuarvoja.
Diskreetin tilastollisen muuttujan jakaumaa kutsutaan diskreetiksi jakaumaksi.
Jakauma
Jakauma ilmaisee muuttujan saamien eri arvojen yleisyyden.
- Absoluuttinen jakauma sisältää havaintoarvot ja niiden esiintymiskertojen lukumäärät eli frekvenssit, \(f\).
- Suhteellinen jakauma sisältää havaintoarvot ja niiden esiintymiskertojen suhteelliset osuudet prosentteina eli suhteelliset frekvenssit, \(f\ \%\).
Esim. 1
Alla olevassa aineistossa on taulukoituna erään abin kaikista pitkän matematiikan opintojaksoista saamat arvosanat.
a) Määritä taulukkolaskentaohjelmalla arvosanoja jakautumista kuvaava absoluuttinen jakauma.
b) Piirrä taulukkolaskentaohjelmalla jakaumaa kuvaava pylväskuvaaja.
c) Määritä taulukkolaskentaohjelmalla arvosanojen suhteellinen jakauma. Ilmoita prosenttiosuudet kokonaisina prosentteina.
d) Määritä laskinohjelmalla arvosanojen absoluuttisen jakauman tunnusluvut: keskiarvo, keskihajonta, mediaani ja moodi.
| Opintojakso | Arvosana |
|---|---|
| MAY1 | 7 |
| MAA2 | 8 |
| MAA3 | 8 |
| MAA4 | 8 |
| MAA5 | 7 |
| MAA6 | 7 |
| MAA7 | 7 |
| MAA8 | 5 |
| MAA9 | 9 |
| MAA10 | 6 |
| MAA11 | 4 |
| MAA12 | 5 |
| MAA13 | 7 |
2.2 Jatkuva muuttuja
Tilastollinen muuttuja on jatkuva, jos se voi saada minkä tahansa arvon tarkasteluvälillä. Esimerkiksi ihmisen pituus voi mittaustarkkuuden rajoissa saada minkä tahansa lukuarvon siltä lukuväliltä, jolla pituus voi vaihdella.
Jatkuvan tilastollisen muuttujan jakaumaa kutsutaan jatkuvaksi jakaumaksi.
Jatkuvia jakaumia on usein luontevinta käsitellä luokiteltuna.
Esim. 1
Eräällä MAB5-opintojaksolla selvitettiin ryhmän opiskelijoiden pituudet. Pituudet ovat taulukoituna alla olevassa aineistossa.
a) Luokittele pituudet neljään tasalevyiseen luokkaan taulukkolaskentaohjelmalla.
b) Määritä luokkien frekvenssit taulukkolaskentaohjelmalla.
c) Määritä arvio pituuksien keskiarvolle ja keskihajonnalle GeoGebralla. Mikä on pituuksien moodiluokka?
Opiskelijoiden pituudet (cm).
| 165 | 157 | 161 | 173 | 167 | 151 | 167 |
| 164 | 185 | 163 | 167 | 172 | 163 | 166 |
| 174 | 173 | 187 | 174 | 163 | 177 | 175 |
| 174 | 173 | 182 | 169 | 184 | 153 | 183 |
| 164 | 173 | 163 | 162 | 164 | 177 | 175 |
Huom.
Luokitellusta aineistoista keskiarvon ja keskihajonnan kaltaisten tunnuslukujen selvittämiseksi on tiedettävä luokkien luokkakeskukset, jotka ovat luokkien todellisten ala- ja ylärajojen keskiarvoja.
Histogrammi
Histogrammi on pylväskuvaaja, jossa pylväät on ovat kiinni toisissaan. Jatkuvaa jakaumaa kuvataan yleensä histogrammilla.
Huom.
Histogrammi piirretään Libre Office Calc -taulukkolaskentaohjelmalla lisäämällä jatkuvalle jakaumalle pylväskaavio ohjattua kaavionluontitoimintoa käyttäen. Kun kaavio on luotu, klikataan vielä hiiren oikealla painikkeella kuvaajan pylvästä ja valitaan Muotoile arvosarja. Asetukset-välilehdeltä muutetaan Objektivälin (Spacing) arvoksi 0 %.
2.3 Kertymä
Kun frekvenssejä lasketaan yhteen saadaan summafrekvenssi, sf. Summafrekvenssi kuvaa, kuinka paljon havaintoja on kertynyt suuruusjärjestyksessä tiettyyn tilastomuuttujan arvoon mennessä.
Suhteellisille frekvensseille voidaan laska suhteellinen summafrekvenssi, sf %.
Luokitellun aineiston mediaaniluokka löydetään etsimällä se luokka, jonka kohdalla suhteellinen summafrekvenssi ylittää 50 prosentin rajan.
Havaintojen kertymää voidaan kuvata kertymäkuvaajalla.
Esim.
Taulukossa on erään MAB5-ryhmän opiskelijoiden pituuksien frekvenssit.
a) Määritä summafrekvenssit, suhteelliset frekvenssit ja suhteelliset summafrekvenssit.
b) Mikä on jakauman mediaaniluokka?
c) Piirrä opiskelijoiden pituuksien kertymäkuvaaja.
| Pituus (cm) | f | sf | f % | sf % |
|---|---|---|---|---|
| 151 - 160 | 3 | |||
| 161 - 170 | 15 | |||
| 171 - 180 | 12 | |||
| 181 - 190 | 5 |
Ratkaisu:
Kopioidaan yllä olevan taulukko LibreOffice Calciin. Lasketaan summafrekvenssit käyttäen soluosoitteita ja yhteenlaskua. Lasketaan suhteelliset frekvenssit aiemmin opitulla tavalla. Lasketaan suhteeliset summafrekvenssit kuten summafrekvenssit. Mediaaniluokka on se luokka, jonka kohdalla saavutetaan 50 %:n raja.
Vastaus: Mediaaniluokka on 161 - 170 cm.
3 RIIPPUVUUS
3.1 Korrelaatio
Korrelaatio tarkoittaa kahden tilastomuuttujan välistä riippuvuutta.
Esim.
Fysiikantunnilla määritettiin opiskelijan kävelynopeutta tutkimalla opiskelijan paikan riippuvuutta ajasta. Opiskelijat saivat seuraavat mittaustulokset.
| Paikka (m) | Aika (s) | 0 | 0,00 |
|---|---|
| 2 | 1,32 |
| 4 | 2,69 |
| 6 | 3,01 |
| 8 | 4,25 |
| 10 | 5,44 |
Opiskelijat sijoittivat mittaustulokset pisteinä koordinaatistoon ja saivat tulokseksi seuraavanlaisen hajontakuvion.
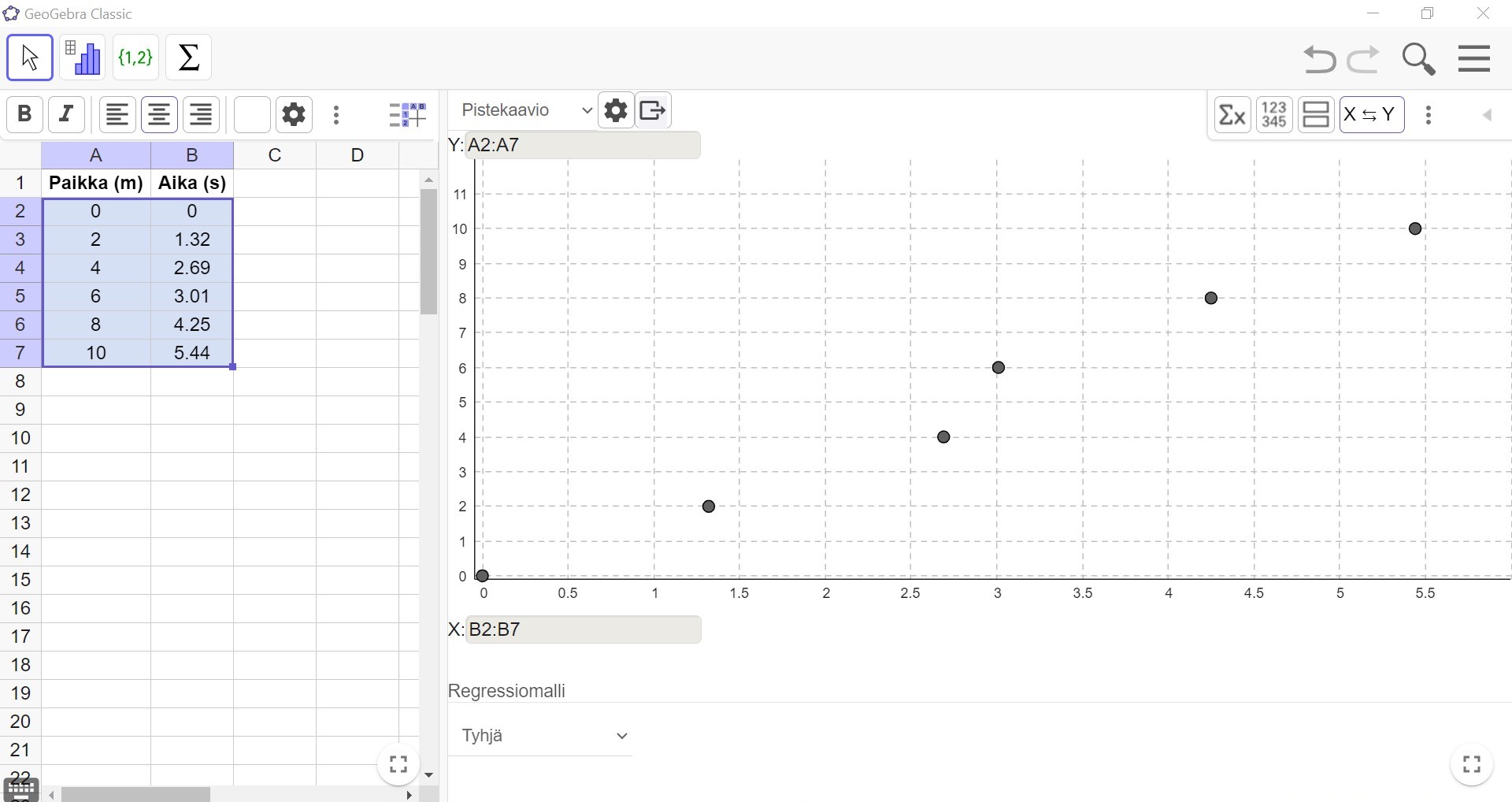
Pisteet sijoittuvat likipitäen samaan nousevaan linjaan. Näyttäisi siis siltä, että ajan ja paikan välillä on lineaarinen (suoraviivainen) riippuvuus. Opiskelijat sovittivat pisteisiin regressiosuoran GeoGebran avulla.
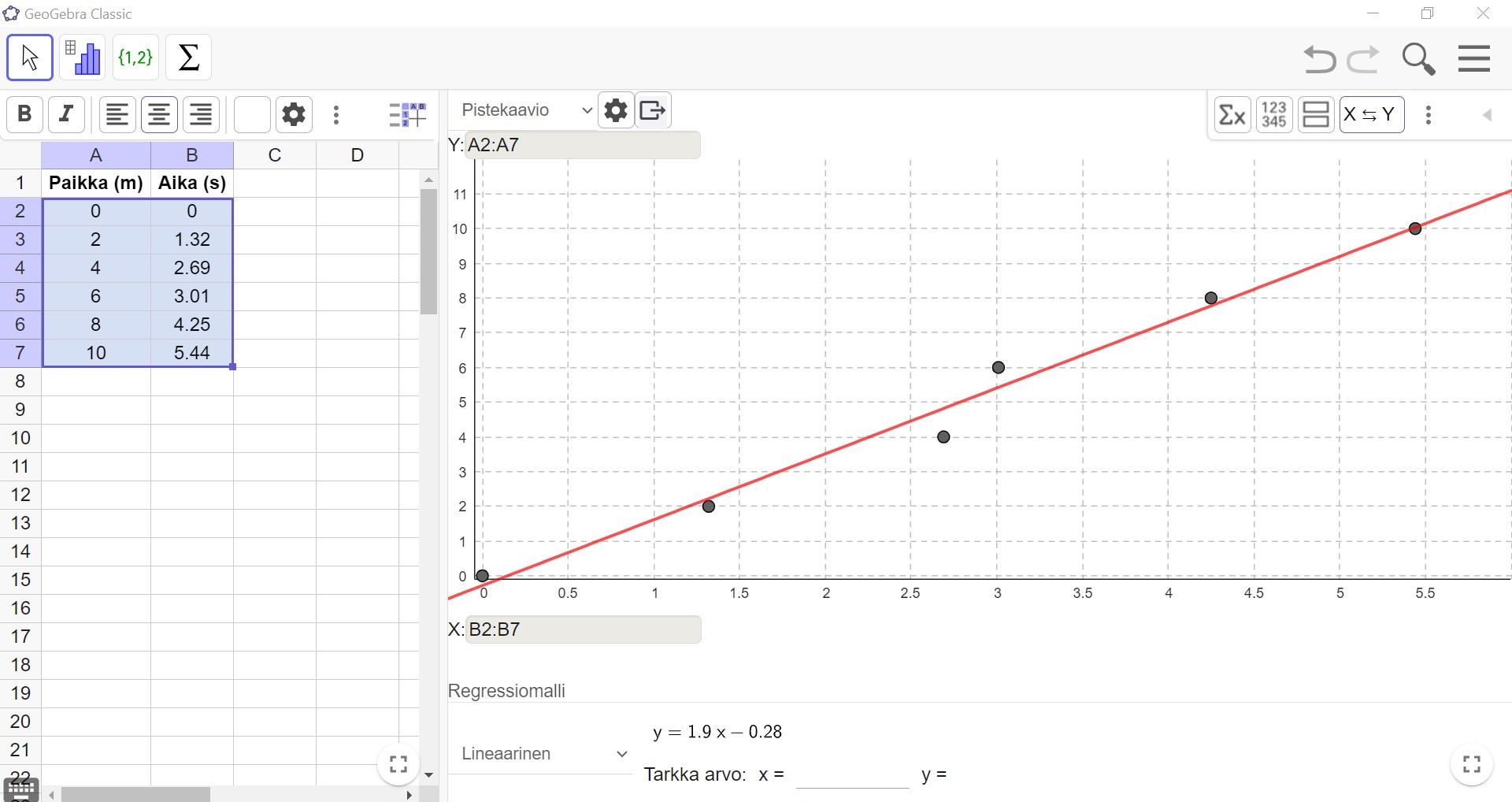
Regressiosuora on lineaarista riippuvuutta kuvaava malli, jolla voidaan ennustaa opiskelijan paikka kunakin ajanhetkenä. Regressiosuoran yhtälö on suoran yhtälön muotoa $$y=ax+b.$$ Jos kulmakerroin \(a>0\), niin suora on nouseva ja puhutaan positiivisesta lineaarisesta riippuvuudesta. Jos kulmakerroin \(a<0\), niin suora on laskeva ja kyseessä on negatiivinen lineaarinen riippuvuus.
Lineaarisen riippuvuuden voimakkuutta voidaan matemaattisesti kuvata korrellaatiokertoimella \(r\). Korrelaatiokertoimen arvo on aina välillä \(-1\leq r\leq 1\). Mitä lähempänä nollaa korrelaatikertoimen arvo on, sitä heikompi on muuttujien välinen riippuvuus. Sanallinen tulkinta eri korrelaatiokertoimen arvoille löytyy esimerkiksi MAOL-taulukoista.
Esimerkin tilanteessa opiskelijan paikan ja ajanhetken välillä on voimakkaan korrelaation lisäksi selvä syy-seuraussuhde. Kaikissa tilanteissa näin ei kuitenkaan ole. Esimerkiksi kesällä aurinkoisina päivinä jäätelöä myydään paljon. Aurinko ei kuitenkaan paista, koska jäätelöä kuluu. Toisaalta pilvisenäkin päivänä kesällä saattaa jäätelöllä olla kysyntää. Kyseessä ei siis ole syy-seuraussuhde. Matemaattisesti syy-seuraussuhteen voimakkuutta voidaan kuvata luvulla selitysaste \(r^{2}\). Selitysaste saadaan lineaariselle mallille korrelaatiokertoimen toisena potenssina. Selitysaste ilmaisee prosentteina, kuinka suurelta osin muuttajan \(x\) arvojen vaihtelu selittää muuttujan \(y\) arvojen vaihtelua.
Lopuksi esimerkin opiskelijat selvittivät vielä uteliaisuuden vuoksi paikan ja ajan väliselle riippuvuudelle GeoGebran avulla korrelaatiokertoimen \(r\) ja selitysasteen \(r^{2}\), vaikka fysiikan tehtävässä niitä ei tarvittukaan.
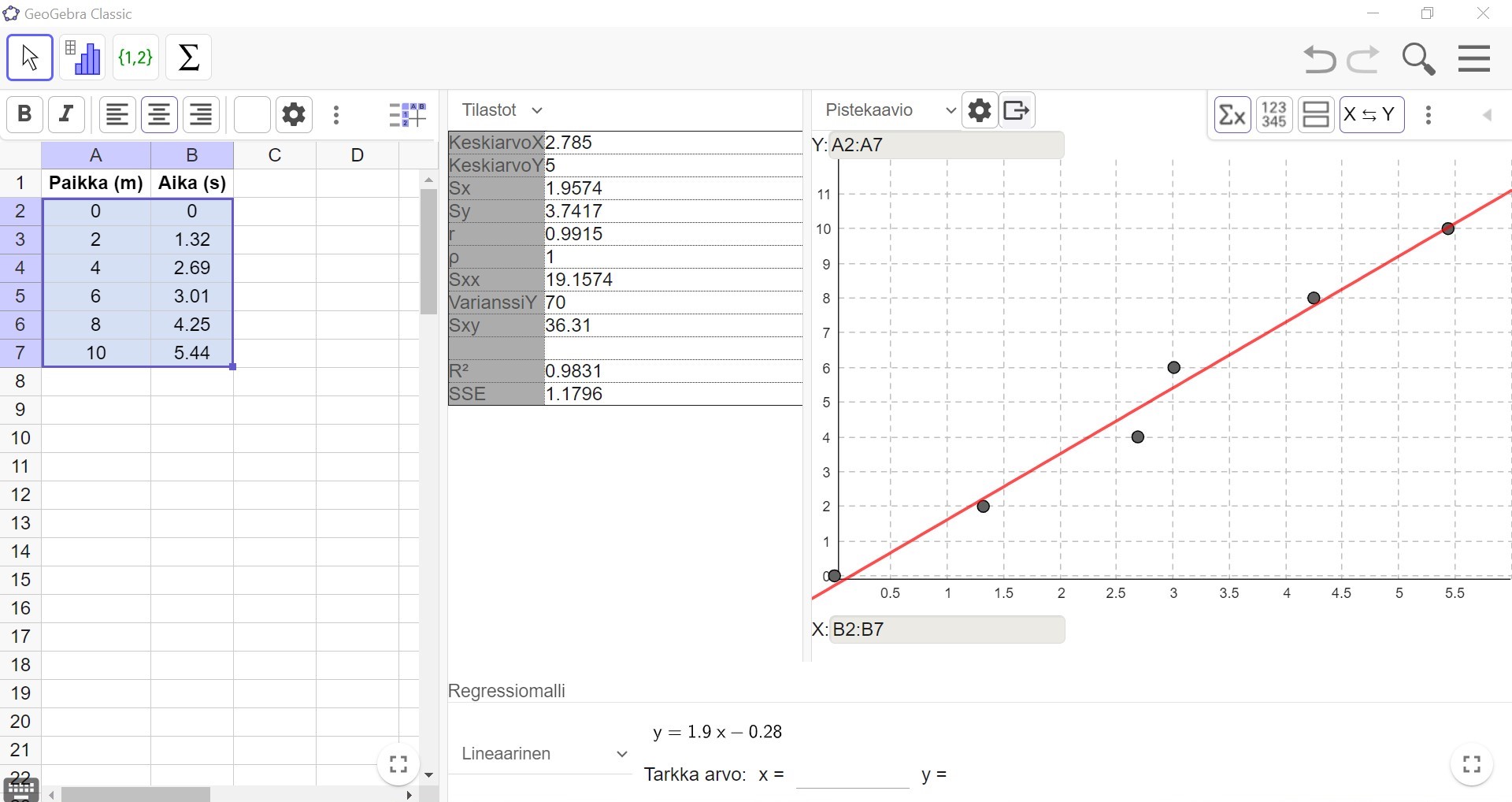
Korrelaatiokerroin oli \(r\approx0{,}99\) ja selitysaste \(r^{2}\approx0{,}98\) eli ajanhetken ja opiskelijan sijainnin välillä on voimakas positiivinen lineaarinen riippuvuus ja aika selittäisi 98 % opiskelijan sijainnista.
3.2 Poikkeava havainto
Poikkeava havainto tarkoittaa havaintoa, joka eroaa muista tilastoaineiston havainnoista. Poikkeavat havainnot voivat vaikuttaa tilaston tulkintaan vääristäen sitä.
Esim. 1
Alla olevassa aineistossa on taulukoituna erään abin kaikista pitkän matematiikan opintojaksoista saamat arvosanat.
a) Mikä on arvosanojen keskiarvo ja keskihajonta.
b) Mikä olisi arvosanojen keskiarvo ja keskihajonta, jos ainoaa arvosanaa 5 ei huomioitaisi.
| Opintojakso | Arvosana |
|---|---|
| MAY1 | 7 |
| MAA2 | 8 |
| MAA3 | 8 |
| MAA4 | 8 |
| MAA5 | 7 |
| MAA6 | 7 |
| MAA7 | 7 |
| MAA8 | 5 |
| MAA9 | 9 |
| MAA10 | 7 |
| MAA11 | 8 |
| MAA12 | 8 |
| MAA13 | 7 |
3.3 Ennuste
Tilastojen perusteella voidaan laatia ennusteita. Ennustuksen luotettavuus riippuu oikean ennustemallin valinnasta ja käytettävissä olevan tiedon (havaintojen) määrästä ja laadusta.
Esim. 1
Alla olevassa aineistossa on Suomen teillä liikennöivien sähköautojen lukumäärät vuosina 2021 - 2024 tarkasteluhetkenä syyskuun loppu. (Lähde: teknologiateollisuus.fi, haettu: 16.12.2024.)
Laadi ennuste sähköautojen lukumäärälle vuoden 2027 syyskuun lopussa. Arvioi ennusteen luotettavuutta.
| Vuosi | Lukumäärä |
|---|---|
| 2021 | 88531 |
| 2022 | 137664 |
| 2023 | 201892 |
| 2024 | 269624 |
Piirretään GeoGebran taulukkolaskennalla hajontakuvio ja sovitetaan regressiokäyrä. Valitaan lineaarinen malli.
Vuotta 2027 vastaa ajanhetki 7.
Sijoitetaan regressiosuoran yhtälöön x=7. Saadaan sähköautojen määräksi noin 447800.
Ennusteen luotettavuus riippuu siitä, onko ennustemalli valittu oikein.
Ennuste olisi luotettavampi, jos käytössä olisi tietoja sähköautojen määrästä usemmalta vuodelta.
4 TODENNÄKÖISYYS
4.1 Klassinen todennäköisyys
Käsitteitä:
- Satunnaisilmiö on tapahtuma, jonka lopputuloksen määrää sattuma.
- Alkeistapaus on satunnaisilmiön eräs mahdollinen lopputulos.
Esim. 1
Nopanheitto on esimerkki satunnaisilmiöstä. Eräs lopputulos eli alkeistapaus on saatu nopan silmäluku. Ilmiöön liittyvät kaikki alkeistapaukset ovat nopan silmäluvut 1, 2, 3, 4, 5 ja 6.
- Alkeistapauksista voidaan muodostaa tapahtumia, joille voidaan määrittää matemaattisesti todennäköisyyksiä.
- Alkeistapauksia, jotka toteuttavat tapahtuman, kutsutaan tapahtumalle suotuisiksi alkeistapauksiksi.
Klassinen todennäköisyys
Klassinen todennäköisyys mallintaa satunnaisilmiöitä, joissa kaikki alkeistapaukset ovat keskenään yhtä mahdollisia eli symmetrisiä.
Tapahtuman \(A\) klassinen todennäköisyys on $$P(A)=\frac{\text{tapahtumalle}\ A\ \text{suotuisat alkeistapaukset}}{\text{kaikki alkeistapaukset}}.$$
Esim. 2
Millä todennäköisyydellä nopanheitossa tulee silmäluvuksi
a) 5
b) vähintään 5?
a) Tapahtumalle "tulee 5" on yksi suotuisa alkeistapaus: silmäluku 5.
$$P(\text{tulee}\ 5)=\frac{1}{6}\textcolor{gray}{=0{,}16666\ldots\approx0{,}167=16{,}7\ \%}$$
b) Tapahtumalle "tulee vähintään 5" on kaksi suotuisaa alkeistapausta: silmäluvut 5 ja 6.
$$P(\text{tulee vähintään}\ 5)=\frac{2}{6}^{(2}=\frac{1}{3}\textcolor{gray}{=0{,}3333\ldots\approx0{,}333=33{,}3\ \%}$$
Huom.
Todennäköisyyden arvo voidaan ilmoittaa murtolukuna, desimaalilukuna tai prosenttilukuna. Klassisille todennäköisyyksille arvot ilmoitetaan useimmiten murtolukuina.
Esim. 3
Korttipakassa on 52 korttia. Millä todennäköisyydellä satunnaisesti nostettu kortti on
a) hertta
b) ässä tai kuningas?
a) Tapahtumalle "tulee hertta" on \(13\) suotuisaa alkeistapausta.
$$P(\text{tulee hertta})=\frac{13}{52}^{(13}=\frac{1}{4}$$
b) Tapahtumalle "tulee ässä tai kuningas" on \(4+4=8\) suotuisaa alkeistapausta.
$$P(\text{tulee ässä tai kuningas})=\frac{8}{52}^{(4}=\frac{2}{13}$$
Huom.
Tapahtuman \(A\) todennäköisyyden arvo on aina \(0\leq P(A)\leq 1\) tai prosentteina \(0\ \%\leq P(A)\leq 100\ \%\).
Tapahtuma, jonka todennäköisyys on \(0 = 0\ \%\), on mahdoton tapahtuma.
Tapahtuma, jonka todennäköisyys on \(1 = 100\ \%\), on varma tapahtuma.
4.2 Tilastollinen todennäköisyys
Tilastollisen todennäköisyyden malli liittyy tilanteisiin, joissa ei voida tarkastella keskenään yhtä todennäköisiä alkeistapauksia, vaan tapahtuman todennäköisyys perustetaan tilastoihin tai kokeellisesti kerättyyn tietoon.
Tilastollinen todennäköisyys
Tapahtuman \(A\) tilastollinen todennälöisyys $$P(A)=\frac{\text{tapahtumalle}\ A\ \text{suotuisat havainnot}}{\text{kaikki havainnot}}.$$
Esim. 1
Millä todennäköisyydellä satunnaisesti valittu pääkaupunkiseudun asukas on vantaalainen?
Esim. 2
Millä todennäköisyydellä satunnaisesti valitun oppilaan arvosana oli vähintään 8?
4.3 Geometrinen todennäköisyys
Kaikkien alkeistapausten lukumäärä voi olla myös ääretön. Tällöin klassisen todennäköisyyden mallia ei voida käyttää. Todennäköisyydelle voidaan kuitenkin määrittää arvo geometristen mittojen (pituus, pinta-ala, tilavuus, kulman suuruus) suhdelukuna.
Geometrinen todennäköisyys
Tapahtuman \(A\) geometrinen todennäköisyys $$P(A)=\frac{\text{tapahtumalle}\ A\ \text{suotuisan joukon mitta}}{\text{perusjoukon mitta}}.$$
Esim. 1
Linja-auto lähtee torin laidalta 15 minuutin välein. Linja-auto avaa ovet matkustajille kolme minuuttia ennen lähtöä. Millä todennäköisyydellä matkustaja
a) saa kävellä suoraan bussiin
b) joutuu odottamaan pysäkillä vähintään kaksi minuuttia ennen ovien avautumista?
a) \(A\) = saa kävellä suoraan bussiin
\(P(A)=\frac{3\ \text{min}}{15\ \text{min}}^{(3}=\frac{1}{5}=0{,}2\)
Vastaus: Matkustaja saa kävellä suoraan bussiin todennäköisyydellä 0,2.
b) \(B\) = joutuu odottamaan vähintään 2 minuuttia
\(P(B)=\frac{10\ \text{min}}{15\ \text{min}}^{(5}=\frac{2}{3}=0{,}666\ldots\approx0{,}67\)
Vastaus: Matkustaja joutuu odottamaan ovien avautumista vähintään 2 minuuttia todennäköisyydellä 0,67.
Esim. 2
Akvaarion pohjan mitat ovat 40 cm x 60 cm. Millä todennäköisyydellä sattumanvaraisesti ripoteltu muru kalanrehua laskeutuu akvaarion pohjalle alle 5 cm päähän akvaarion seinästä?
Merkitään \(A\) = rehumuru laskeutuu alle \(5\ \text{cm}\) päähän seinästä.
Tapahtumalle \(A\) suotuisan joukon mitta = pinta-ala alueelle, joka on alle 5 cm päässä akvaarion seinästä: $$2\cdot5\ \text{cm}\cdot 60\ \text{cm}+2\cdot5\ \text{cm}\cdot 30\ \text{cm}=900\ \text{cm}.$$
Perusjoukon mitta = pohjan pinta-ala: $$40\ \text{cm}\cdot 60\ \text{cm}=2400\ \text{cm}.$$
Tapahtuman \(A\) todennäköisyys:
$$P(A)=\frac{900\ \text{cm}}{2400\ \text{cm}}=0{,}375$$
Vastaus: Rehumuru laskeutuu alle 5 cm päähän akvaarion seinästä todennäköisyydellä 0,375.
5 LASKUSÄÄNTÖJÄ
5.1 Kertolaskusääntö
Tapahtumat ovat riippumattomia, jos ne eivät vaikuta toisiinsa.
Riippumattomien tapahtumien kertolaskusääntö ( ja-sääntö)
Todennäköisyys riippumattomien tapahtumien tapahtumiselle yhdessä saadaan kertomalla tapahtumien todennäköisyydet keskenään.
Esim. 1
Millä todennäköisyydellä kahden nopan heitossa saadaan kaksi kuutosta?
Merkitään:
\(A\) = ''1. nopalla tulee kuutonen''
\(B\) = ''2. nopalla tulee kuutonen''
Todennäköisyys tapahtumalle ''tulee kaksi kuutosta'' eli ''tapahtuu \(A\) \(\text{ja}\) \(B\)'' (riippumattomia):
\(P(A\ \text{ja}\ B)=P(A)\cdot P(B)=\frac{1}{6}\cdot\frac{1}{6}=\frac{1}{36}\).
Vastaus: Kaksi kuutosta saadaan todennäköisyydellä \(\frac{1}{36}\).
Esim. 2
Sääennusteen mukaan ensimmäisenä päivänä sateen todennäköisyys on 40 % ja toisena päivänä 80 %. Millä todennäköisyydellä molempina päivinä sataa?
Merkitään:
\(A\) = ''1. päivänä sataa''
\(B\) = ''2. päivänä sataa''
Todennäköisyys tapahtumalle ''molempina päivinä sataa'' eli ''tapahtuu \(A\) \(\text{ja}\) \(B\)'' (riippumattomia):
\(P(A\ \text{ja}\ B)=P(A)\cdot P(B)=0{,}4\cdot 0{,}8=0{,}32\)
Vastaus: Molempina päivinä sataa \(32\ \%\) todennäköisyydellä.
Esim. 3
Kielten kuuntelussa oli monivalintatehtävä, jonka viidessä tehtäväkohdassa kussakin oli neljä vastausvaihtoehtoa. Millä todennäköisyydellä sattumanvaraisesti vastaten saa kaikki kohdat
a) oikein
b) väärin?
a) Todennäköisyys tapahtumalle kaikki oikein (riippumattomia, kertolaskusääntö):
\(P(\text{kaikki oikein})=\frac{1}{4}\cdot \frac{1}{4}\cdot \frac{1}{4}\cdot \frac{1}{4}\cdot \frac{1}{4} =\left(\frac{1}{4}\right)^{5}=\frac{1}{1024}\)
Vastaus: Kaikki oikein saadaan todennäköisyydellä \(\frac{1}{1024}\).
b) Todennäköisyys tapahtumalle kaikki väärin (riippumattomia, kertolaskusääntö):
\(P(\text{kaikki väärin})=\frac{3}{4}\cdot \frac{3}{4}\cdot \frac{3}{4}\cdot \frac{3}{4}\cdot \frac{3}{4} =\left(\frac{3}{4}\right)^{5}=\frac{243}{1024}\)
Vastaus: Kaikki oikein saadaan todennäköisyydellä \(\frac{243}{1024}\).
5.2 Yhteenlaskusääntö
Tapahtumat ovat erillisiä eli toisensa poissulkevia, jos niillä ei ole yhteisiä alkeistapauksia. Kaksi tapahtumaa ovat erillisiä, jos toisen tapahtuessa toinen ei voi tapahtua.
Esim. 1
Korttipakasta nostetaan kortti. Ovatko tapahtumat erillisiä?
a) ''tulee pata'' tai ''tulee ässä''
b) ''tulee pata'' tai ''tulee hertta''?
a) Tapahtumat eivät ole erilliset, koska tapahtumat voivat tapahtua yhtä aikaa ("tulee pataässä").
Vastaus: Ei.
a) Tapahtumat ovat erilliset, koska tapahtumat eivät voi tapahtua yhtä aikaa (eli ei ole korttia, joka olisi yhtä aikaa pata ja hertta).
Vastaus: Kyllä.
Erillisten tapahtumien yhteenlaskusääntö (tai-sääntö)
Todennäköisyys erillisistä tapahtumista vähintään yhden tapahtumiselle saadaan laskemalla tapahtumien todennäköisyydet yhteen.
Esim. 2
Laske todennäköisyys esimerkin 1 erillisille tapahtumille.
On laskettava todennäköisyys, että nostettaessa korttipakasta kortti tulee pata tai hertta.
Merkitään:
\(A\) = ''tulee pata''
\(B\) = ''tulee hertta''
Todennäköisyys tapahtumalle ''tulee pata tai hertta'' eli ''tapahtuu \(A\) \(\text{tai}\) \(B\)'' (erilliä):
\(P(A\ \text{tai}\ B)=P(A)+ P(B)=\frac{13}{52}+\frac{13}{52}=\frac{26}{52}^{(26}=\frac{1}{2}\)
Vastaus: Todennäköisyys, että tulee pata tai hertta on \(\frac{1}{2}\).
Esim. 3
Sääennusteen mukaan ensimmäisenä päivänä sateen todennäköisyys on 40 % ja toisena päivänä 80 %. Millä todennäköisyydellä vain yhtenä päivistä sataa?
On laskettava todennäköisyys, että joko ensimmäisenä tai toisena päivänä sataa, mutta ei molempina.
Merkitään:
\(A\) = ''1. päivänä sataa''
\(B\) = ''2. päivänä sataa''
Todennäköisyys tapahtumalle ''vain yhtenä päivänä sataa'' eli ''tapahtuu \((A\ \text{ja}\ \text{ei}\ B)\ \text{tai}\ (\text{ei}\ A\ \text{ja}\ B)\)'':
\(P\left((A\ \text{ja}\ \text{ei}\ B)\ \text{tai}\ (\text{ei}\ A\ \text{ja}\ B)\right)\)
\(=P(A)\cdot P(\text{ei}\ B)+P(\text{ei}\ A)\cdot P(B)\)
\(=0{,}4\cdot0{,}2+0{,}6\cdot0{,}8\)
\(=0{,}08+0{,}48\)
\(=0{,}56\)
Vastaus: Todennäköisyys, että vain yhtenä päivänä sataa on \(56\ \%\).
5.3 Vastatapahtuma
Tapahtuman ''tapahtuu \(A\)'' vastatapahtuma eli komplementtitapahtuma on ''ei tapahdu \(A\)''.
Tapahtuman \(A\) vastatapahtumaa merkitään \(\bar{A}\).
Esim. 1
Päättele vastatapahtuma.
a) Kolikonheitossa tulee klaava.
b) Yksittäisen nopan heitossa tulee kuutonen.
c) Heitettäessä kolmea noppaa tulee kolme kuutosta.
a) Kolikonheitossa tapahtuman ''tulee klaava'' vastatapahtuma on ''ei tule klaava'' eli ''tulee kruuna''.
b) Yksittäisen nopan heitossa tapahtuman ''tulee kuutonen'' vastapahtuma on ''ei tule kuutonen'' eli ''tulee ykkönen tai kakkonen tai kolmonen tai nelonen tai viitonen''.
c) Heitettäessä kolmea noppaa tapahtuman ''tulee kolme kuutosta'' vastatapahtuma on "ainakin yksi ei ole kuutonen''.
Tapahtuma ja sen vastatapahtuma ovat erilliset ja sisältävät yhdessä kaikki perusjoukon alkeistapaukset. Siten tapahtuman todennäköisyyden ja vastatapahtuman todennäköisyyden summa on yksi eli varma tapahtuma: $$P(A) + P(\bar{A})=1.$$ Näin ollen tapahtuman todennäköisyys voidaan ilmoittaa vastatapahtuman avulla: $$P(A)=1-P(\bar{A}).$$
Toisinaan jonkin tapahtuman todennäköisyys onkin helpompi laskea vastatapahtumaa hyödyntäen.
Esim. 2
Millä todennäköisyydellä viidellä nopalla heitettäessä tulee ainakin yksi kuutonen?
Tapahtuma ''tulee ainakin yksi kuutonen'' on varsin monimutkainen. On helpompaa laskea todennäköisyys vastatapahtumaa ''ei tule yhtään kuutosta'' hyödyntäen.
$$ \begin{align} P(''\text{tulee ainakin yksi kuutonen}'')&=1-P(''\text{ei tule yhtään kuutosta}'')\\ &=1-\frac{5}{6}\cdot\frac{5}{6}\cdot\frac{5}{6}\cdot\frac{5}{6}\cdot\frac{5}{6}\\ &=1-\left(\frac{5}{6}\right)^{5}\\ &=0{,}59812\approx 0{,}598\\ \end{align} $$
Vastaus: 0,598
6 VAIHTOEHTOJEN LUKUMÄÄRÄ
6.1 Tuloperiaate
Jos tapahtuma sisältää vaiheita, joissa jokaisessa suoritetaan valintoja useasta eri vaihtoehdosta, saadaan tapahtuman kaikkien mahdollisten alkeistapausten lukumäärä kertomalla eri vaiheissa olevien vaihtoehtojen lukumäärät keskenään.
Esim.
Milkalla on kaksi takkia, kolmet housut ja kaksi paria kenkiä. Kuinka monta eri asukokonaisuutta Milka vaatteista saa?
Ratkaisu:
Tapa 1: Puumalli
Puun piirrustaminen aloitetaan ''latvasta''. Kaikkien alkeistapausten lukumäärä luetaan puun ''juuresta''.
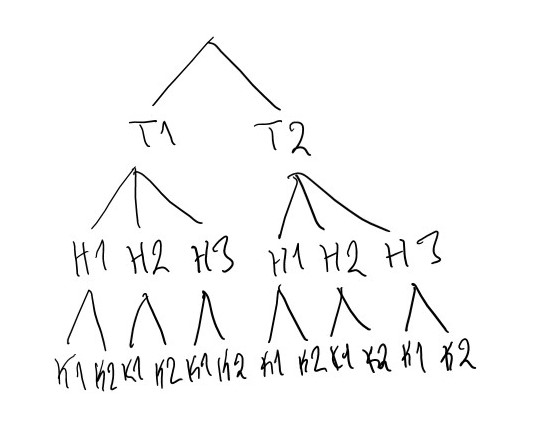
Tapa 2: Tuloperiaate
Ensimmäisessä vaiheessa Milka voi valita kahdesta takista, toisessa vaiheessa valinta jatkuu kolmien housujen väliltä ja kolmannessa vaiheessa valitaan kengät vielä kahdesta parista. Kaikkien mahdollisten asukokonaisuuksien lukumäärä saadaan kertomalla eri vaiheiden valintojen vaihtoehtojen lukumäärät keskenään: $$2\cdot 3\cdot 2=12.$$
Vastaus: 12 eri asukokonaisuutta.
6.2 Kertoma
Kertoma on laskutoimitus, jolla voidaan laskea, kuinka moneen eri järjestykseen jonon jäsenet voidaan järjestää.
Esim.
a) Kuinka monella eri tavalla viisi opiskelijaa voi järjestäytyä jonoon?
b) Millä todennäköisyydellä opiskelijat järjestäyvät sattumalta pituusjärjestykseen lyhimmästä pisimpään?
Ratkaisu:
a) Jonon ensimäinen jäsen voidaan valita viidestä vaihtoehdosta, toinen neljästä, kolmas kolmesta, neljäs kahdesta ja viimeiselle paikalle jää jäljelle yksi. Tuloperiaatteen mukaan eri vaiheiden vaihtoehtojen lukumäärät kerrotaan keskenään: $$5\cdot 4\cdot 3\cdot 2\cdot 1=\underbrace{5!}_{\text{luvun 5 kertoma}}=120.$$
Vastaus: Opiskelijat voivat järjestäytyä jonoon 120 eri tavalla.
b) Opiskelijat järjestäyvät pituusjärjestykseen todennäköisyydellä $$\frac{1}{120}=0{,}008333\dots\approx0{,}00833.$$
Vastaus: Todennäköisyys on 0,00833.
6.3 Osajoukkojen lukumäärä
Osajoukkojen lukumäärä tarkoittaa, kuinka monta \(k\)-jäsenen ryhmää voitaisiin muodostaa \(n\)-jäsenen joukosta.
Tälle on oma laskutoimitus, joka merkitään $$\binom{n}{k}.$$ Merkintä luetaan \(n\) yli \(k\):n ja se näppäillään esimerkikiksi SpeedCrunch-laskimeen ncr(n;k).
Esim.
Kuinka monta kahden oppiskelijan paria voidaan voidaan muodostaa viiden opiskelijan joukosta?
Ratkaisu:
Parien lukumäärä saadaan laskemalla:
$$\binom{5}{2}=10.$$
(Näppäily laskimeen ncr(5;2).)
Vastaus: Viiden opiskelijan joukosta voidaan muodostaa 10 erilaista paria.