Talousmatematiikka (MAB7)
Laajuus
1 op
Yleiset tavoitteet (LOPS 2021)
Moduulin tavoitteena on, että opiskelija
- oppii hyödyntämään matemaattisia valmiuksiaan resurssien riittävyyteen, talouden suunnitteluun, yrittäjyyteen ja kannattavuuden laskentaan
- soveltaa lukujonojen kaavoja talouteen liittyvissä matemaattisissa ongelmissa
- oppii sovittamaan taloudellisiin tilanteisiin matemaattisia malleja ja ymmärtää niiden rajoitukset
- osaa hyödyntää ohjelmistoja laskelmien tekemisessä ja sovellusten yhteydessä.
Keskeiset sisällöt (LOPS 2021)
- aritmeettinen ja geometrinen lukujono ja niiden summat
- korkolaskut: koron korko, nykyarvo ja diskonttaus
- talletukset ja lainat
- taloudellisiin tilanteisiin soveltuvia matemaattisia malleja, joissa hyödynnetään lukujonoja ja summia
Aikataulu
Suoritus
- osallistuminen
- tehtävien tekeminen
- monivalintatehtävien tekeminen
- loppukoe
Arviointi
- säännöllinen, aktiivinen ja vastuullinen osallistuminen +1 p
- tehtävien asianmukainen ja jatkuva tekeminen +1 p
- monivalintatehtävistä +1 p kustakin tehdystä monivalintakokonaisuudesta, saavutettava tavoitetaso 80 %, yht. max. 3 p
- loppukokeesta max. 36 p
- max. 40 p (teoreettisesti 41 p)
- 30 % arviointi
| Pisteet | Arvosana | Muuta |
|---|---|---|
| 0 - 6 | i \(\rightarrow\) K | Pakko täydentää. |
| 7 - 11 | i \(\rightarrow\) 4 | Oikeus täydentää. |
| 12 - 17 | 5 | |
| 18 - 23 | 6 | |
| 24 - 29 | 7 | |
| 30 - 35 | 8 | |
| 36 - 38 | 9 | |
| 39 - 40 | 10 |
Keskeyttäminen
Opettaja keskeyttää opiskelijan opintojakson, jos
- opiskelija niin pyytää
- opiskelija ei ole läsnä opintojakson kahdella ensimmäisellä opetuskerralla ja opiskelija ei ole yhteydessä opettajaan eikä opettaja saa yhteyttä opiskelijaan.
Opettaja voi keskeyttää opiskelijan opintojakson, jos opiskelijalla on viisi poissaoloa. Tällaiset tilanteet opettaja käy läpi tapauskohtaisesti ja on ennen lopullista keskeytystä yhteydessä opiskelijaan.
Keskeyttämisestä opettaja merkitsee opintojaksosta opiskelijalle K-merkinnän Wilmaan ja poistaa opiskelijan sen jälkeen Wilman ryhmästä. Opettaja lähettää keskeyttämisestä viestin opiskelijalle, alaikäisen opiskelijan huoltajalle, ryhmänohjaajalle ja opolle.
1 KORKO
2.1 Kertausta
Korko on toisaalta pankin talletuksesta maksama korvaus ja toisaalta pankin lainasta perimä hinta.
Sanastoa
Pääoma = talletussumma.
Korkoprosentti eli korkokanta = pääomasta korkojaksolta kertyvä prosenttiosuus. Ellei toisin mainita korkojakso on yksi vuosi, jolloin voidaan käyttää myös nimitystä vuosikorko.
Lähdevero = pankin korkotulosta automaattisesti vähentämä ja valtiolle tilittämä vero. Lähdevero on 30 % korkotulosta ja se pyöristetään alaspäin lähimpään 10 senttiin.
Nettokorko eli todellinen korko = korko, josta on vähennetty tallettamiseen liittyvät kustannukset, kuten esimerkiksi tilinhoitomaksu ja lähdevero.
Nimelliskorko = inflaation vaikutusta ei ole huomioitu.
Reaalikorko = inflaation vaikutus on huomioitu.
Esim. 1
Vuoden alussa talletetaan 800 euroa tilille, jonka vuosikorko on 3,1 %.
Laske
a) koron määrä
b) rahan määrä tilillä koron maksun ja lähdeveron pidätyksen jälkeen.
a) Koron määrä:
\(3{,}1\ \%=0{,}031\)
\(0{,}031\cdot800=24{,}80\)
Vastaus: 24,80 euroa.
b) Lähdevero:
\(30\ \%=0{,}3\)
\(0{,}3\cdot24{,}80=7{,}44\approx7{,}40\) Huom. Lähdeveron pyöristys.
Rahan määrä tilillä:
\(800+24{,}80-7{,}40=817{,}40\)
Vastaus: 817,40 euroa.
Esim. 2
Laske esimerkin 1 tilanteen
a) nettokorkokanta
b) reaalikorkokanta, kun inflaatio on 0,7 %.
a) Nettokorkokanta (huomioi lähdeveron pidätyksen vaikutuksen):
Lähdevero on \(30\ \%\).
Jäljelle jäävä koron osuus on siten
\(100\ \%-30\ \%=70\ \%=0{,}7\).
Nettokorkokanta on siis
\(0{,}7\cdot0{,}031=0{,}0217=2{,}17\ \%\)
Vastaus: 2,17 %.
b) Reaalikorkokanta (huomioi inflaation vaikutuksen):
Nettokorkokerroin on
\(100\ \%+2{,}17\ \%=102{,}17\ \%=1{,}0217\).
Inflaatiokerroin on
\(100\ \%+0{,}7\ \%=100{,}7\ \%=1{,}007\).
Reaalikorkokerroin on tällöin
\(\displaystyle{\frac{1{,}0217}{1{,}007}}=1{,}01459\ldots\approx1{,}0146\)
ja reaalikorkanta
\(0{,}0146=1{,}46\ \%\).
Vastaus: 1,46 %.
Vuotta lyhyemmältä ajalta korko lasketaan seuraavasti.
Yksinkertainen korko
Kun korkoaika on lyhyempi tai yhtä pitkä kuin yksi korkojakso, korko \(r\) lasketaan
\(r=kit\),
missä
- \(k\) on pääoma,
- \(i\) on vuotuinen korkokanta desimaalilukuna ja
- \(t\) on korkoaika vuosina.
Korkoaika vuosina voidaan laskea eri korkotapoja käyttäen.
Merkitään talletuspäivien lukumäärää \(n\).
| Korkotapa | Päiviä kuukaudessa | Päiviä vuodessa | Aika vuosina |
|---|---|---|---|
| englantilainen | kalenterin mukaan | \(365\ (366)\) | \(t=\frac{n}{365}\ \left(t=\frac{n}{366}\right)\) |
| ranskalainen | kalenterin mukaan | \(360\) | \(t=\frac{n}{360}\) |
| saksalainen | 30 | \(360\) | \(t=\frac{n}{360}\) |
Jos tehtävässä ei muuta mainita, käytetään saksalaista korkotapaa.
1.2 Yksinkertainen korko taulukkolaskennalla
Esim. 1.
Talletetaan tammikuusta joulukuuhun joka kuukauden alussa 100 € tilille, jonka vuosikorko on 2,9 %. Kuinka paljon tililtä voidaan nostaa rahaa vuoden lopussa? Lähdeveron pyöristystä ei tarvitse huomioida.
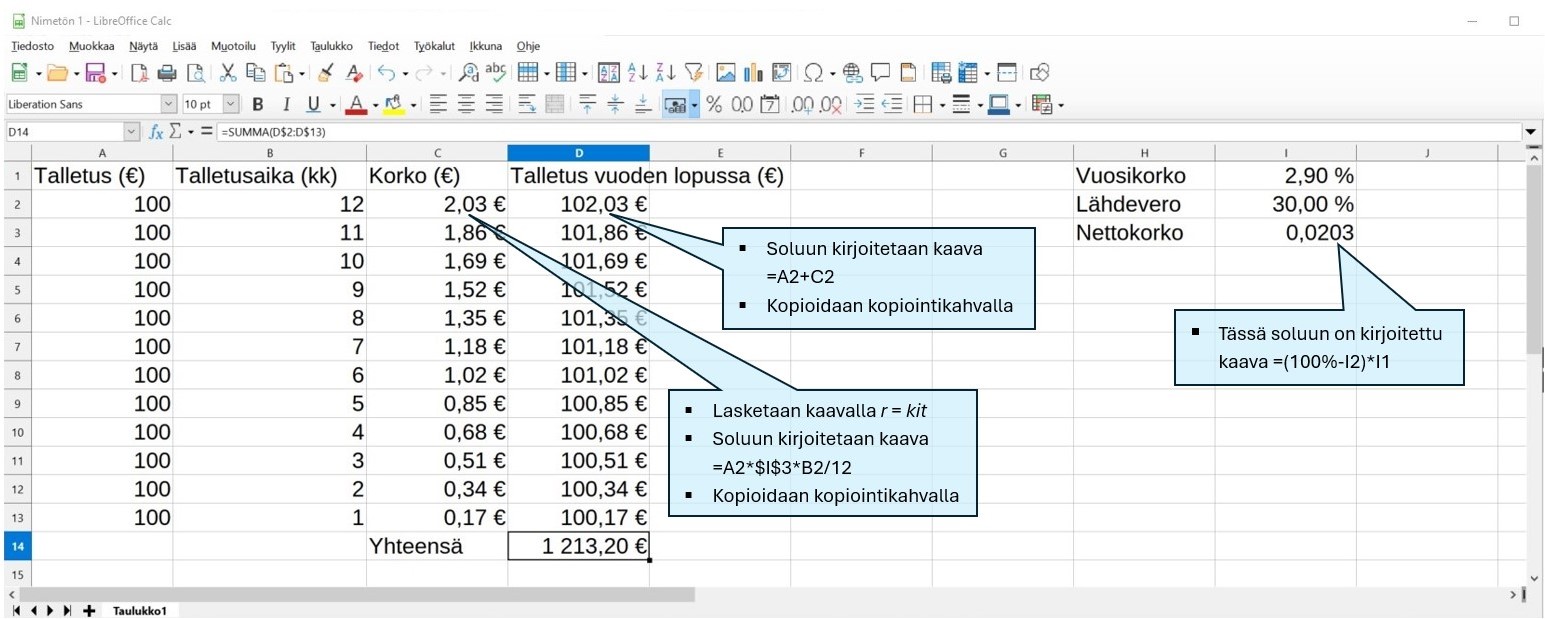
Vastaus: 1213,20 euroa.
1.3 Koron korko
Koron korko on ilmiö, jossa talletukselle maksettu korko tuottaa korkoa, kun korkoaika on pitempi kuin korkojakso.
Esim. 1
Määritä uusi pääoma yhden, kahden, kolmen ja \(n\) vuoden kuluttua, kun alkupääoma on 2 000 € ja vuosikorko 2,0 %.
\(\begin{array}{c|lll} \text{aika (vuosi)}&\text{uusi pääoma (euroa)}\\ \hline 1&2000\cdot1{,}02&=2000\cdot1{,}02^1&=2040\\ 2&2000\cdot1{,}02\cdot1{,}02&=2000\cdot1{,}02^2&=2080{,}80\\ 3&2000\cdot1{,}02\cdot1{,}02\cdot1{,}02&=2000\cdot1{,}02^3&=2122{,}416\\ \vdots&\vdots\\ n&2000\cdot\underbrace{1{,}02\cdot1{,}02\cdot\ldots\cdot1{,}02}_{n\ \text{kappaletta}}&=2000\cdot1{,}02^n \end{array}\)
Koron korko
Jos korkokanta pysyy samana, niin uusi pääoma \(K_{n}\) on \(n\) vuoden kuluttua
$$K_{n}=Kq^{n},$$
missä \(K\) on alkupääoma ja \(q\) on korkotekijä (-kerroin).
Esim. 2
Arin isä talletti Arille \(1000\) euroa sen vuoden, jona Ari syntyi, alussa.
a) Kuinka paljon tilillä on rahaa Arin täyttäessä \(18\) vuotta, jos nettokorkokanta pysyy \(3\) %:ssa?
b) Kuinka monen vuoden kuluttua tilillä olisi yli \(2000\) euroa?
c) Mikä olisi nettokorkokannan oltava, jotta tilillä olisi yli \(3000\) euroa Arin täyttäessä 25 vuotta?
a) Rahan määrä tilillä Arin täyttäessä 18 vuotta:
\(\begin{align} K&=1000\\ q&=100\ \%+3\ \%=103\ \%=1{,}03\\ n&=18\\ \\ K_n&=Kq^n\\ \\ K_{18}&=1000\cdot1{,}03^{18}\\ &=1702{,}43306\ldots\\ &\approx1702{,}43 \end{align}\)
Vastaus: 1702,43 €.
b) Monenko vuoden kuluttua tilillä olisi yli 2000 euroa:
\(\begin{align} K_n&=2000\\ K&=1000\\ q&=100\ \%+3\ \%=103\ \%=1{,}03\\ \\ K_n&=Kq^n\\ \\ 2000&=1000\cdot1{,}03^{n}\quad\mid\text{CAS-laskin}\\ n&=23{,}449\ldots\\ &\approx23{,}4 \end{align}\)
Lukua 23,4 suurempi seuraava kokonaisluku on 24. 2000 euron raja on ylittynyt 24. vuoden loppuun mennessä.
Vastaus: 24 vuoden kuluttua.
c) Kysytty nettokorkokanta:
\(\begin{align} K_n&=3000\\ K&=1000\\ n&=25\\ \\ K_n&=Kq^n\\ \\ 3000&=1000\cdot q^{25}\quad\mid\text{CAS-laskin}\\ q&=1{,}04492\ldots\\ &\approx1{,}045 \end{align}\)
Nettokorkokannan on oltava 4,5 %.
Vastaus: 4,5 %.
Esim. 3
Elia tallettaa kesätöistä säästyneitä rahoja neljänä peräkkäisenä vuonna aina uuden vuoden alkaessa säästötilille, jonka nettokorkokanta on 3,0 %. Jokainen talletus on 500 euroa. Kuinka paljon tilillä on rahaa viiden vuoden kuluttua ensimmäisestä talletuksesta?
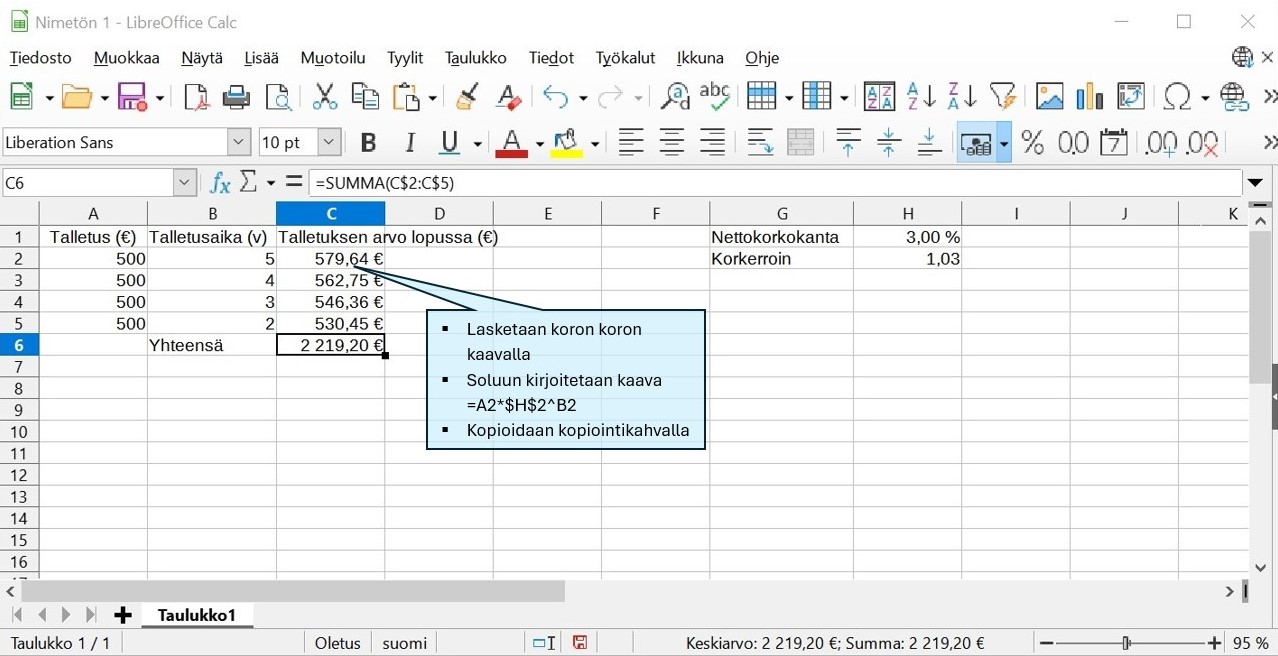
Vastaus: 2219,20 euroa.
1.4 Diskonttaus
Diskonttaus on koron lisäämiselle käänteinen toimitus.

Alkupääoma \(K\) voidaan ratkaista koron koron kaavasta
\(K_{n}=Kq^{n}\),
kun tunnetaan uusi pääoma \(K_n\), korkokerroin \(q\) ja talletusaika \(n\).
Esim. 1
Kuinka suuri alkupääoma on sijoitettava, jotta \(3\) % nettovuosikorolla uusi pääoma olisi \(4\) vuoden kuluttua \(5000\) euroa?
\(\begin{align} K_n&=5000\\ q&=100\ \%+3\ \%=103\ \%=1{,}03\\ n&=4\\ \\ K_n&=Kq^n\\ \\ 5000&=K\cdot1{,}03^{4}\quad\mid\text{CAS-laskin}\\ K&=4442{,}43523\ldots\\ &\approx4442{,}44 \end{align}\)
Vastaus: 4442,44 €.
Esim. 2
Pekka sai ylioppilaslahjaksi summan rahaa.
Pekka laski, että jos hän sijoittaa rahat korkeakorkoiselle tilille (vuosikorko \(3{,}1\) %), hän voi vuoden kuluttua nostaa tililtä \(100\) €, kahden kuluttua \(200\) € ja kolmen kuluttua \(500\) €.
Kuinka paljon rahaa Pekka sai ylioppilaslahjaksi?
2 LUKUJONO
2.1 Lukujono
Lukujono on järjestetty kokoelma lukuja. Sama luku voi esiintyä jonossa määräämättömän monta kertaa.
Esim. 1
Lukujonot \(1,2,3,4\) ja \(4,3,2,1\) eivät ole sama lukujono, koska jonojen jäsenten järjestys ei ole sama.
Lukujono voi olla päättyvä, jolloin jonon jäsenten määrä on äärellinen, tai päättymätön, jolloin taas jonon jäsenten määrä on ääretön.
Esim. 2
Lukujono \(1,3,5,7\) on päättyvä.
Lukujono \(1,3,5,\ldots\) on päättymätön.
Merkintöjä
Lukujono merkitään \((a_{n})\).
Jonon jäseniä merkitään \(a_{1},a_{2},a_{3},\dots\) . Indeksointi alkaa yleensä ykkösestä (voi alkaa myös nollasta).
Jonon \(n\):s eli yleinen jäsen merkitään \(a_n\). Merkinnällä voidaan viitata myös \(n\):nnen jäsenen lausekkeeseen.
Lukujono voidaan määritellä:
analyyttisesti antamalla jonon \(n\):nnen jäsenen lauseke
rekursiivisesti ilmoittamalla jonon ensimmäinen jäsen ja antamalla lauseke seuraavan jäsenen laskemiseksi.
Esim. 3
Olkoon lukujono \((a_{n})\), missä \(n\):nnen jäsenen lauseke on \(a_{n}=n^{2}+1\) ja \(n=1,2,3,\ldots\) .
a) Määritä jonon kolme ensimmäistä jäsentä.
b) Määritä jonon sadas jäsen.
c) Onko luku \(145\) jonon jäsen? Jos on, monesko jäsen se on?
a) Jonon kolme ensimmäistä jäsentä ovat:
\(a_{1}=1^{2}+1=2\)
\(a_{2}=2^{2}+1=5\)
\(a_{3}=3^{2}+1=10\)
b) Jonon sadas jäsen on:
\(a_{100}=100^{2}+1=10\ 001\)
c) Luku \(145\) on jonon jäsen, jos on olemassa positiivinen kokonaisluku \(n\), jolla \(a_{n}=n^{2}+1=145\).
Ratkaistaan yhtälö \(n^{2}+1=145\) tuntemattoman \(n\) suhteen:
$$\begin{align} n^{2}+1&=145\quad\mid\ -1\\ n^{2}&=144 \quad\mid\ \sqrt{\ }\\ n&=\pm12 \end{align}$$
Luvun \(n\) on oltava positiivinen kokonaisluku. Siis \(n=12\).
Vastaus: Luku \(145\) on jonon \(12.\) jäsen.
Esim. 4
Olkoon lukujono \((a_{n})=\begin{cases}a_{1}=3&\\a_{n}=2a_{n-1}+1,&\text{kun}\ n=2,3,4,\ldots\end{cases}\).
Määritä lukujonon viisi ensimmäistä jäsentä.
Jonon viisi ensimmäistä jäsentä ovat:
\(a_{1}=3\)
\(a_{2}=2\cdot3+1=7\)
\(a_{3}=2\cdot7+1=15\)
\(a_{4}=2\cdot15+1=31\)
\(a_{5}=2\cdot31+1=63\)
Huom.
Funktio \(f\) voidaan määritellä myös lukujonona \(f(n)=a_{n}\), jolloin jonon jäsenten järjestysnumerot eli alaindeksit \(n=1,2,3\dots\) vastaavat muuttujan arvoja ja jonon jäsenet \(a_{n}\) vastaavia funktion arvoja.
Esim. 5
Määritä taulukkolaskentaohjelmalla lukujonon \((a_n)\) kymmenes jäsen ja kymmenen ensimmäisen jäsenen summa.
a) \(a_{n}=n^{2}+1,\ \text{kun}\ n=1,2,3,\ldots\)
b) \(a_{n}=\begin{cases}a_{1}=3&\\a_{n}=2a_{n-1}+1,&\text{kun}\ n=2,3,4,\ldots\end{cases}\)
a) Kirjoitetaan ensimmäiseen sarakkeeseen jonon jäsenten järjestysnumerot. Toiseen sarakkeeseen lasketaan jonon jäseniä yleisen jäsenen lausekkeen avulla.
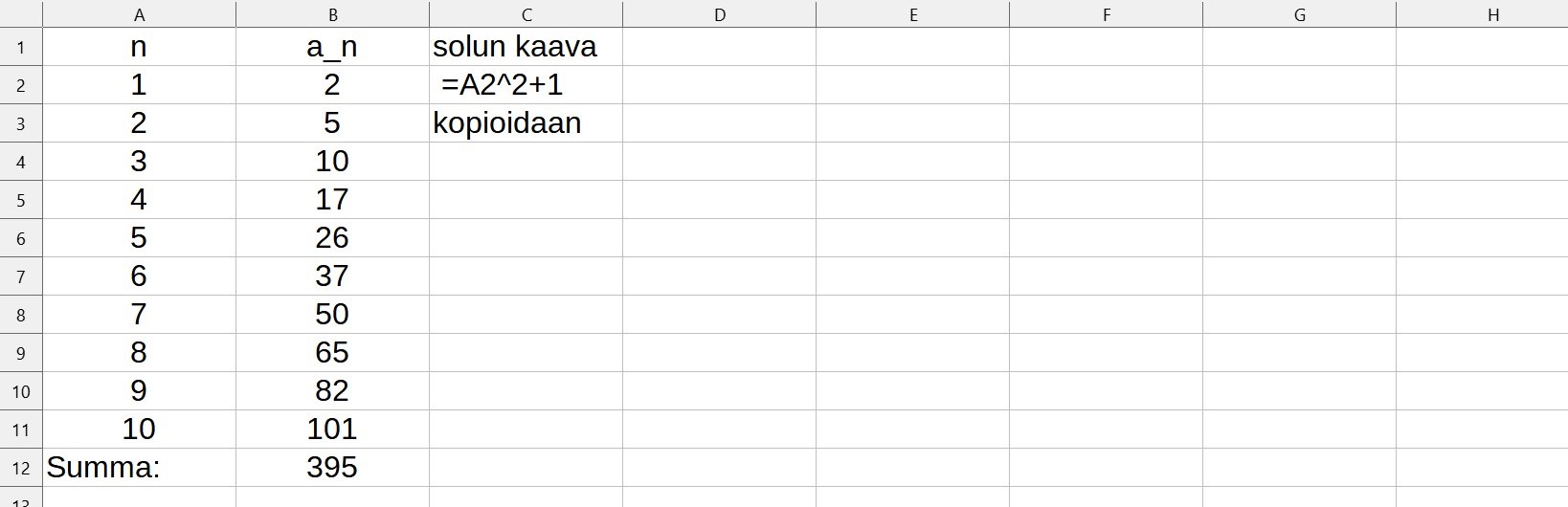
Vastaus: \(a_{10}=101\), \(S_{10}=395\)
b) Kirjoitetaan ensimmäiseen sarakkeeseen jonon jäsenten järjestysnumerot. Toiseen sarakkeeseen merkitään jonon ensimmäinen jäsen ja toisesta jäsenestä alkaen lasketaan jonon jäseniä.
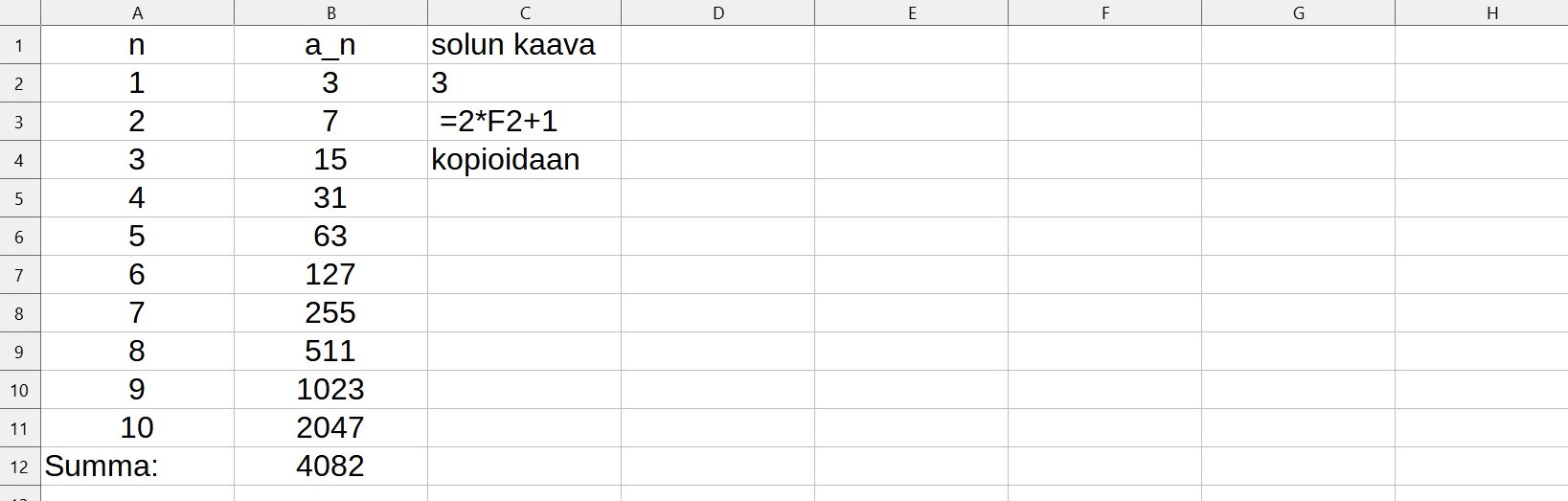
Vastaus: \(a_{10}=2047\), \(S_{10}=4082\)
2.2 Aritmeettinen lukujono
Aritmeettinen lukujono on jono, jonka seuraava jäsen saadaan edellisestä lisäämällä aina sama luku.
Esim. 1
\(1\overset{\overset{+3}{\curvearrowright}}{,\ \ 4}\overset{\overset{+3}{\curvearrowright}}{,\ \ 7}\overset{\overset{+3}{\curvearrowright}}{,\ 10},\ldots\) .
Määritelmä
Lukujono on aritmeettinen, jos sen peräkkäisten jäsenten erotus on vakio
$$d=a_{n}-a_{n-1} .$$ Vakiota \(d\) kutsutaan lukujonon erotusluvuksi.
Esim. 2
Olkoon lukujono \((a_{n})=1,3,5,7,\ldots\) . Voiko lukujono olla aritmeettinen?
Määritetään peräkkäisten jäsenten erotukset.
\(3-1=2\)
\(5-3=2\)
\(7-5=2\)
\(\qquad\ \vdots\)
Vastaus: Koska erotusluku on aina 2, lukujono voi olla aritmeettinen.
Aritmeettisen lukujonon jäsenet saadaan ensimmäisestä jäsenestä lisäämällä siihen erotusluvun \(d\) monikerta.
Aritmeettisen lukujonon yleisen (\(n\):nnen) jäsenen lauseke
$$a_{n}=a_{1}+(n-1)d .$$
Esim. 3
Olkoon lukujono \((a_{n})=38,34,30,\ldots\) .
a) Voiko jono olla aritmeettinen?
b) Jos jono olisi aritmeettinen, muodosta jonon yleisen jäsenen lauseke ja laske jonon \(20.\) jäsen.
c) Kuinka moni jonon jäsenistä on positiivisia?
a) Jono on aritmeettinen, jos peräkkäisten jäsenten erotus on vakio.
\(34-38=-4\)
\(30-34=-4\)
Vastaus: Annettujen peräkkäisten jäsenten erotus on aina \(d=-4\), joten jono voi olla aritmeettinen.
b) Jonon yleinen jäsen:
\(\begin{align}a_{n}&=a_{1}+(n-1)d\qquad\ \mid \text{sij.}\ a_{1}=38\ \text{ja}\ d=-4\\ &=38+(n-1)\cdot(-4)\\ &=38-4n+4\\ &=42-4n\end{align}\)
Jonon \(15.\) jäsen:
\(a_{15}=42-4\cdot15=-18\)
Vastaus: \(a_{n}=42-4n\) ja \(a_{15}=-18\)
c) Lukujonon jäsen on positiivinen, jos se on suurempi kuin 0. Saadaan epäyhtälö:
\(\begin{align}a_{n}&\gt 0\\ 42-4n&\gt 0\quad\quad\ \mid\ -42\\ -4n&\gt -42\quad\mid\ :(-4)\\ n&\lt 10{,}5\end{align}\)
Suurin positiivinen kokonaisluku, joka toteuttaa epäyhtälön on \(10\). Jonon kymmenen ensimmäistä jäsentä ovat siis positiivisia.
Vastaus: \(10\) jäsenistä on positiivisia.
Esim. 4*
Olkoon jono \((a_{n})\), missä \(a_{n}=5n-2\). Osoita, että jono on aritmeettinen.
2.3 Aritmeettinen summa
Aritmeettinen summa on aritmeettisen lukujonon peräkkäisten jäsenten yhteenlaskun tulos.
Esim. 1
Aritmeettisen lukujonon \(1,4,7,10, \ldots\) neljän ensimmäisen jäsenen summa on \(1+4+7+10=22\).
Merkintä
Aritmeettisen lukujonon \(a_{1},a_{2},a_{3},\ldots\) \(n\):n ensimmäisen jäsenen summa merkitään $$S_{n}=a_{1}+a_{2}+a_{3}+\ldots+a_{n} .$$
Aritmeettisen lukujonon \(n\):n peräkkäisen jäsenen summa voidaan laskea luvun \(n\) sekä ensimmäisen ja viimeisen huomioitavan jäsenen keskiarvon tulona.
Aritmeettisen summan laskukaava
$$S_{n}=n\cdot\frac{a_{1}+a_{n}}{2}$$
Huom.
Pitkiä summalausekkeita voidaan lyhentää summamerkinnän avulla.
Summamerkintä
$$\sum_{k=1}^{n}a_{k}=a_{1}+a_{2}+a_{3}+\ldots+a_{n}$$
Merkintä luetaan ''summa \(k\) käy yhdestä \(n\):ään''. Merkintä tarkoittaa, että lasketaan yhteen jonon \(a_{n}\) jäseniä. Summamerkin alapuolelta luetaan, mistä jäsenestä aloitetaan, ja yläpuolelta, mihin lopetetaan.
Esim. 2*
Tulkitse summamerkintä \(\displaystyle{\sum_{k=2}^{5}(2k+1)}\).
Esim. 3
Olkoon aritmeettinen jono \((a_{n})\), missä \(a_{n}=5n-2\).
Laske
a) \(S_{10}\)
b) \(\displaystyle{\sum_{k=5}^{30}(a_{n})}\)
Esim. 4*
Laske aritmeettinen summa \(23+26+29+\ldots+122\).
2.4 Geometrinen lukujono
Geometrinen lukujono on jono, jonka seuraava jäsen saadaan edellisestä kertomalla aina samalla luvulla.
Esim. 1
\(1\overset{\overset{\cdot3}{\curvearrowright}}{,\ \ 3}\overset{\overset{\cdot3}{\curvearrowright}}{,\ \ 9}\overset{\overset{\cdot3}{\curvearrowright}}{,\ 27},\ldots\) .
Määritelmä
Lukujono on geometrinen, jos sen peräkkäisten jäsenten osamäärä eli suhde on vakio
$$q=\frac{a_{n}}{a_{n-1}} .$$ Vakiota \(q\) kutsutaan lukujonon suhdeluvuksi.
Huom.
Erityistapaus, jossa \(a_{1}\) on mikä tahansa reaaliluku, voi olla myös nolla, ja \(q=0\), tuottaa jonon \(a_{1},0,0,\ldots\) .
Esim. 2
Olkoon lukujono \((a_{n})=5,10,20,40,\ldots\) . Voiko lukujono olla geometrinen?
Määritetään peräkkäisten jäsenten suhteet eli jakolaskut.
\(\frac{10}{5}=2\)
\(\frac{20}{10}=2\)
\(\frac{40}{20}=2\)
\(\quad\ \ \vdots\)
Vastaus: Koska suhdeluku on aina 2, lukujono voi olla geometrinen.
Geometrisen lukujonon jäsenet saadaan ensimmäisestä jäsenestä kertomalla se suhdeluvun \(q\) potenssilla.
Geometrisen lukujonon yleisen (\(n\):nnen) jäsenen lauseke
$$a_{n}=a_{1}q^{n-1} .$$
Esim. 3
Olkoon geometrinen lukujono \((a_{n})=2,8,32,\ldots\) .
a) Määritä jonon yleisen jäsenen lauseke
b) Laske jonon \(10.\) jäsen.
a) Määritetään suhdeluku \(q\):
\(q=\frac{a_{n}}{a_{n-1}}=\frac{8}{2}=4\)
Määritetään jonon yleinen jäsen:
\(\begin{align} a_{n}&=a_{1}q^{n-1}\qquad\ \ \mid\ \text{sij.}\ a_{1}=2\ \text{ja}\ q=4\\ &=2\cdot4^{n-1}\end{align}\)
Vastaus: Yleisen jäsenen lauseke on \(a_{n}=2\cdot4^{n-1}\).
b) Jonon \(10.\) jäsen:
\(a_{10}=2\cdot4^{10-1}=2\cdot4^{9}=524\ 288\)
Vastaus: \(a_{10}=524\ 288\).
2.5 Geometrinen summa
Geometrinen summa on geometrisen lukujonon peräkkäisten jäsenten yhteenlaskun tulos.
Esim. 1
Geometrisen lukujonon \((a_{n})=1,3,9,27,\ldots\) neljän ensimmäisen jäsenen summa on \(S_{4}=1+3+9+27=40\).
Geometrinen summa
Geometrisen lukujonon \(a_{1},a_{2},a_{3},\ldots\) \(n\):n ensimmäisen jäsenen summa $$\begin{align} S_{n}&=a_{1}+a_{2}+a_{3}+\ldots+a_{n}\\ &=\sum_{k=1}^{n}a_{k}\\ &=\frac{a_{1}\left(1-q^{n}\right)}{1-q} , \end{align}$$ jos suhdeluku \(q\neq1\) ja $$S_n=na_1,$$ jos suhdeluku \(q=1\).
Esim. 2
Geometrisen lukujonon ensimmäinen jäsen on \(1\) ja suhdeluku \(3\).
Laske
a) \(S_{12}\)
b) \(\displaystyle{\sum_{n=4}^{9}a_{n}}\)
Esim. 3
Kuinka monta geometrinen lukujonon \((a_{n})=1,3,9,27,\ldots\) jäsentä alusta lukien on laskettava yhteen, jotta summa ylittää arvon \(5\ 000\).
2.6 Sovelluksia
Osavuoden korko kuukausittaisille talletuksille voidaan laskea aritmeettisen summan avulla.
Esim. 1
Tilille, jonka nettokorkokanta on 2,4 %, talletetaan 100 euroa joka kuun ensimmäinen päivä huhtikuun alusta vuoden loppuun asti.
a) Kuinka paljon tilillä on rahaa vuoden lopussa koron maksun jälkeen?
b) Mikä olisi kuukausittaisen talletussumman oltava, että tilillä olisi rahaa vuoden lopussa 2000 euroa?
Koron korko vuosittaisille talletuksille voidaan laskea geometrisen summan avulla.
Esim. 2
Arin isä talletti Arille 1000 euroa Arin syntymävuoden alussa, ja joka vuoden alussa kunnes Ari täytti 16 vuotta. Tilin nettokorkokanta oli 2,5 %.
a) Kuinka paljon tilillä on rahaa Arin täyttäessä \(18\) vuotta?
b) Mikä olisi vuosittaisen talletussumman oltava, että tilillä olisi rahaa Arin 18-vuotispäivänä 30 000 euroa?
3 LAINA
3.1 Laina
Sanastoa
Korko = lainan hinta. Lainan korolla voidaan tarkoittaa toisaalta lainan vuosikorkoa prosentteina tai toisaalta lainan lyhentämisen yhteydessä maksettavaa koron määrää euroina.
Lainapääoma = jäljellä olevan lainan määrä.
Lyhennys = rahasumma, jolla lainaa maksetaan takaisin eli lainapääomaa lyhennetään.
Takaisinmaksuerä = lyhennys ja korko yhteensä.
Lisätietoa
Korkoprosentti muodostuu viitekorosta (Euribor tai Prime) ja korkomarginaalista.
Todellinen vuosikorko on prosentteina ilmoitettava korko, joka pitää sisällään kaikki lainan hoitoon liittyvät kustannukset.
3.2 Tasalyhennyslaina
Tasalyhennyslaina on maksetaan takaisin yhtä suurina lyhennyksinä. Lyhennysjaksolta (usein kuukausi) maksetaan lyhennyksen lisäksi korko jäljellä olevasta lainapääomasta. Näin ollen takaisinmaksuerä pienenee, kun lainapääoma vähenee.
Esim. 1
Remonttia varten otettiin 18 000 euron laina. Laina on tasalyhennyslaina, jota lyhennetään kuukausittain. Laina-aika on 3 vuotta. Lainan korko on 3,4 %.
a) Mikä on takaisinmaksuerien lukumäärä?
b) Kuinka suuri on kertalyhennys?
c) Kuinka suuri on ensimmäinen takaisinmaksuerä? Entä viimeinen?
d) Kuinka paljon lainaa on jäljellä 2 vuoden kuluttua?
a) Takaisinmaksuerien lukumäärä:
\(3\cdot12=36\)
Vastaus: 36.
b) Kertalyhennyksen suuruus:
\(\displaystyle{\frac{18000}{36}=500}\)
Vastaus: 500 €.
c) Ensimmäinen takaisinmaksuerä (lyhennys + korko):
\(500+18000\cdot0{,}034\cdot\frac{1}{12}=551\)
Viimeinen takaisinmaksuerä (lyhennys + korko):
\(500+500\cdot0{,}034\cdot\frac{1}{12}=501{,}41666\ldots\approx501{,}42\)
Vastaus: Ensimmäinen takaisinmaksuerä on 551 € ja viimeinen 501,42 €.
d) Lyhennykset:
\(2\cdot12=24\) (kk)
\(24\cdot500=12000\) (€)
Jäljellä:
\(18000-12000=6000\) (€)
Vastaus: 6 000 €.
Esim. 2
Laadi esimerkin 1 tilanteesta takaisinmaksusuunnitelma. Kuinka paljon korkoa lainasta maksetaan yhteensä, jos korko säilyisi samana koko laina-ajan?
Esimerkin 1 perusteella kertalyhennyksen suuruus on 500 €.

Vastaus: 943,50 €.
3.3 Tasaerä- eli annuiteettilaina
Tasaerä- eli annuiteettilainassa takaisinmaksuerät ovat yhtä suuria. Näin ollen, jos korkokanta säilyy samana, laina-ajan kuluessa ja lainapääoman vähentyessä takaisinmaksuerästä lyhennyksen osuus on yhä suurempi ja koron osuus yhä pienempi.
Usein ajan kuluessa korkokanta kuitenkin vaihtuu. Tällöin joko laina-ajan pituus muuttuu takaisinmaksuerän pysyessä vakiona (kiinteäeräinen annuiteetti) tai takaisinmaksuerän suuruus muuttuu laina-ajan pysyessä vakiona (kiinteäaikainen annuiteetti).
Tasaerän eli annuiteetin laskeminen
$$A=Kq^{n}\frac{1-q}{1-q^{n}}$$
Kaavassa
- \(A\) = tasaerän suuruus,
- \(K\) = lainapääoma alussa,
- \(n\) = tasaerien (takaisinmaksukertojen) lukumäärä ja
- \(q\) = yhden lyhennysjakson korkokerroin.
Tasaerälainan jäljellä olevan lainapääoman laskeminen
$$V_{k}=Kq^{k}-A\frac{1-q^{k}}{1-q}$$
Kaavassa
- \(k\) = maksettujen tasaerien lukumäärä,
- \(V_{k}\) = lainapääoma \(k\):n lyhennyksen jälkeen,
- \(K\) = lainapääoma alussa,
- \(A\) = tasaerän suuruus ja
- \(q\) = yhden lyhennysjakson korkokerroin.
Huom.
Annuiteetin laskukaavoissa korkotekijä \(q\) on määritettävä lyhennysjaksolle.
Esim. 1
Lainan vuosikorko on 2,4 %. Laske korkokerroin, kun lyhennysjakso on
a) vuosi
b) puoli vuotta
c) kuukausi.
a) \(q=100\ \%+2{,}4\ \%=102{,}4\ \%=1{,}024\).
b) \(q=100\ \%+\displaystyle{\frac{2{,}4\ \%}{2}}=100\ \%+1{,}2\ \%=101{,}2\ \%=1{,}012\).
c) \(q=100\ \%+\displaystyle{\frac{2{,}4\ \%}{12}}=100\ \%+0{,}2\ \%=100{,}2\ \%=1{,}002\).
Esim. 2
Remonttia varten otettiin 18 000 euron laina. Laina on tasaerä- eli annuiteettilaina, jota lyhennetään kuukausittain. Laina-aika on 3 vuotta. Lainan korko on 3,6 %.
a) Kuinka suuri on takaisinmaksuerä eli annuiteetti?
b) Kuinka paljon korkoa lainasta maksetaan yhteensä?
c) Kuinka paljon lainaa on jäljellä 2 vuoden kuluttua?
a) Takaisinmaksuerän suuruus lasketaan kaavalla:
\(A=Kq^{n}\displaystyle{\frac{1-q}{1-q^{n}}}\).
\(K=18000\)
\(q=100\ \%+\displaystyle{\frac{3{,}6\ \%}{12}}=100\ \%+0{,}3\ \%=100{,}3\ \%=1{,}003\)
\(n=3\cdot12=36\)
Takaisinmaksuerän suuruus on
\( \begin{align} A&=18000\cdot1{,}003^{36}\cdot\displaystyle{\frac{1-1{,}003}{1-1{,}003^{36}}}\\ &=528{,}2348...\\ &\approx528{,}23 \end{align} \)
Vastaus: 528,23 €
b) 36 lyhennyskerralla maksetaan yhteensä:
\(36\cdot528{,}23=19016{,}28\) (€).
Korkojen määrä on siten
\(19016{,}28-18000=1016{,}28\) (€).
Vastaus: 1016,28 €
c) Jäljellä olevan laina määrä lasketaan kaavalla:
\(V_{k}=Kq^{k}-A\displaystyle{\frac{1-q^{k}}{1-q}}\).
\(K=18000\)
\(q=100\ \%+\displaystyle{\frac{3{,}6\ \%}{12}}=100\ \%+0{,}3\ \%=100{,}3\ \%=1{,}003\)
\(k=2\cdot12=24\)
\(A=528{,}23\) (a-kohdan perusteella)
\( \begin{align} V_{k}&=18000\cdot1{,}003^{24}-528{,}23\cdot\displaystyle{\frac{1-1{,}003^{24}}{1-1{,}003}}\\ &=6217{,}0412...\\ &\approx6217{,}04 \end{align} \)
Vastaus: 6217,04 €
Esim. 3
Laadi esimerkin 2 tilanteesta takaisinmaksusuunnitelma. Minkä takia korkojen määrä eroaa esimerkin 2 tuloksesta?
Esimerkin 2 perusteella takaisinmaksuerän suuruus on 528,23 €.
