Tilastolliset ja todennäköisyysjakaumat (MAB9)
Laajuus
2 op
Yleiset tavoitteet (LOPS 2021)
Moduulin tavoitteena on, että opiskelija
- tutustuu normaalijakaumaan matemaattisena mallina
- tutustuu binomijakaumaan matemaattisena mallina
- vahvistaa ja monipuolistaa tilastojen käsittely- ja tutkimustaitojaan ohjelmistojen avulla
- tietää, kuinka lasketaan tilastollisiin jakaumiin liittyviä tunnuslukuja ja todennäköisyyksiä, ja osaa määrittää ne ohjelmistojen avulla
- ymmärtää luottamusvälin ja virhemarginaalin käsitteen ja osaa määrittää ne ohjelmistojen avulla.
Keskeiset sisällöt (LOPS 2021)
- normaalijakauma ja jakauman normittamisen käsitteet (odotusarvo ja keskihajonta)
- toistokoe
- binomijakauma
- luottamusvälin ja virhemarginaalin käsite
Aikataulu
Suoritus
- osallistuminen
- oppikirjan tehtävien tekeminen
- kaksi harjoitustehtävää
- loppukoe
Arviointi
- säännöllinen, aktiivinen ja vastuullinen osallistuminen +1 p
- enintään neljä poissaoloa
- tehtävien asianmukainen ja jatkuva tekeminen +3 p
- vähintään yksi asianmukaisesti tehty oppikirjan tehtävä käytössä ollutta oppituntia kohden
- tarkistetaan kahden viikon jaksoissa
- harjoitustehtävät 2 x 12 p = 24 p
- loppukoe 6 x 12 p = 72 p
- yhteensä max. 100 p
- 30 % arviointi
Arvosanataulukko
| Pisteet | Arvosana | Muuta |
|---|---|---|
| 0 - 14 | i \(\to\) K | Pakko täydentää. |
| 15 - 29 | 4 | Oikeus täydentää. |
| 30 - 42 | 5 | |
| 43 - 55 | 6 | |
| 56 - 68 | 7 | |
| 69 - 81 | 8 | |
| 82 - 94 | 9 | |
| 95 - 100 | 10 |
Keskeyttäminen
Opettaja keskeyttää opiskelijan opintojakson, jos
- opiskelija niin pyytää
- opiskelija ei ole läsnä opintojakson kahdella ensimmäisellä opetuskerralla ja opiskelija ei ole yhteydessä opettajaan eikä opettaja saa yhteyttä opiskelijaan.
Opettaja voi keskeyttää opiskelijan opintojakson, jos opiskelijalla on neljä poissaoloa. Tällaiset tilanteet opettaja käy läpi tapauskohtaisesti ja on ennen lopullista keskeytystä yhteydessä opiskelijaan.
Keskeyttämisestä opettaja merkitsee opintojaksosta opiskelijalle K-merkinnän Wilmaan ja poistaa opiskelijan sen jälkeen Wilman ryhmästä. Opettaja lähettää keskeyttämisestä viestin opiskelijalle, alaikäisen opiskelijan huoltajalle, ryhmänohjaajalle ja opolle.
1 KERTAUSTA TILASTOISTA
1.1 Tilastollinen tutkimus
Tilasto on valikoitu ja järjestetty kokoelma tietoa, joka perustuu tilastollisella tutkimuksella kerättyyn havaintoaineistoon.
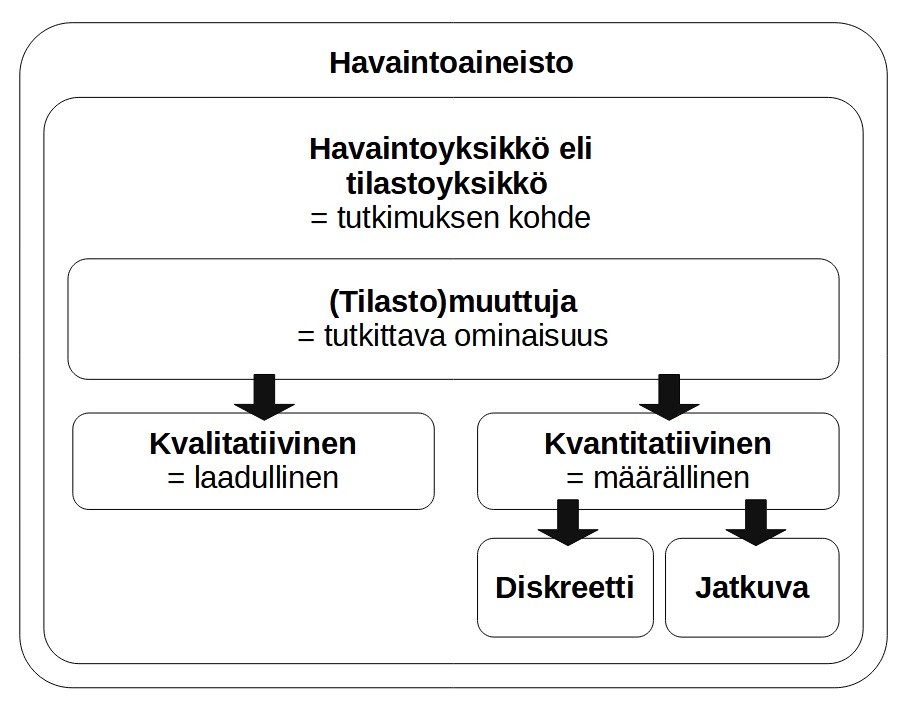
Tilastollisessa tutkimuksessa mitataan muuttujan saamia vaihtelevia havaintoarvoja.
Jakauma
Jakauma ilmaisee muuttujan saamien eri havaintoarvojen yleisyyden.
- Absoluuttinen jakauma sisältää havaintoarvot ja niiden esiintymiskertojen lukumäärät eli frekvenssit, \(f\).
- Suhteellinen jakauma sisältää havaintoarvot ja niiden esiintymiskertojen suhteelliset osuudet prosentteina eli suhteelliset frekvenssit, \(f\ \%\).
1.2 Diskreetti tilastojakauma
Tilastollinen muuttuja on diskreetti, jos se saa erillisiä arvoja, esimerkiksi kokonaislukuarvoja.
Diskreetin tilastollisen muuttujan jakaumaa kutsutaan diskreetiksi jakaumaksi.
Esim. 1
Alla olevassa aineistossa on taulukoituna erään abin kaikista pitkän matematiikan opintojaksoista saamat arvosanat.
a) Määritä taulukkolaskentaohjelmalla arvosanoja jakautumista kuvaava absoluuttinen jakauma. Piirrä absoluuttista jakaumaa kuvaava pylväskuvaaja.
b) Määritä taulukkolaskentaohjelmalla arvosanojen suhteellinen jakauma. Ilmoita prosenttiosuudet kokonaisina prosentteina. Piirrä suhteellista jakaumaa kuvaava pylväskuvaaja.
| Opintojakso | Arvosana |
|---|---|
| MAY1 | 7 |
| MAA2 | 8 |
| MAA3 | 8 |
| MAA4 | 8 |
| MAA5 | 7 |
| MAA6 | 7 |
| MAA7 | 7 |
| MAA8 | 5 |
| MAA9 | 9 |
| MAA10 | 6 |
| MAA11 | 4 |
| MAA12 | 5 |
| MAA13 | 7 |
1.3 Tilastolliset tunnusluvut
Tilastoon sisältyvää tietoa voidaan tiivistää tilastollisten tunnuslukujen avulla.
Keskiluvut
Keskiluvut kuvaavat jakauman keskikohtaa.
Keskilukuja ovat muun muassa:
Moodi
Moodi eli tyyppiarvo on tilaston eniten esiintyvä havaintoarvo (suurin frekvenssi). Jos suurin frekvenssi esiintyy useilla havaintoarvoilla, ne kaikki ovat tyyppiarvoja.
Mediaani
Mediaani on tilaston suuruusjärjestyksessä keskimmäinen havaintoarvo silloin, kun havaintoarvoja on pariton määrä. Jos havaintoarvoja on parillinen määrä, mediaani on kahden keskimmäisen keskiarvo.
Keskiarvo
Keskiarvo on havaintoarvojen summa jaettuna havaintoarvojen lukumäärällä.
$$\bar{x}=\frac{x_{1}+x_{2}+\ldots+x_{n}}{n}=\frac{\sum_{i=1}^{n}x_{i}}{n},$$
missä \(x_{1}, x_{2},\ldots, x_{n}\) ovat havaintoarvoja ja \(n\) havaintoarvojen lukumäärä.
Hajontaluvut
Hajontaluvut kuvaavat, kuinka paljon havaintoarvot vaihtelevat keskiarvon ympärillä.
Hajontalukuja ovat muun muassa:
Vaihteluväli
Vaihteluväli ilmaistaan ilmoittamalla tilaston pienin ja suurin havaintoarvo.
Vaihteluvälin pituus
Vaihteluvälin pituus on tilaston suurimman ja pienimmän havaintoarvon erotus.
Keskihajonta
Keskihajonta kuvaa, miten havaintoarvot ovat jakautuneet keskiarvon ympärille. Mitä lähempänä nollaa keskihajonnan arvo on, sitä lähemmäksi keskiarvoa havaintoarvot tilastossa sijoittuvat.
Esim. 1
Määritä havaintoaineiston 8, 7, 9, 10, 9, 6, 9 mediaani, moodi, keskiarvo, vaihteluväli ja vaihteluvälin pituus.
Tunnusluvut laskinohjelmilla
GeoGebran komentoja
- havaintoarvojen lukumäärä
=Pituus() - moodi eli tyyppiarvo
=Tyyppiarvo() - mediaani
=Mediaani() - keskiarvo
=Keskiarvo() - keskihajonta
=Keskihajonta() - otoskeskihajonta
=Otoskeskihajonta() - pienin arvo
=Min() - suurin arvo
=Max()
LibreOffice Calc -ohjelman komentoja
- havaintoarvojen lukumäärä
=LASKE.A() - moodi eli tyyppiarvo
=MOODI.USEA() - mediaani
=MEDIAANI() - keskiarvo
=KESKIARVO() - keskihajonta
=KESKIHAJONTA.P() - otoskeskihajonta
=KESKIHAJONTA.S() - pienin arvo
=MIN() - suurin arvo
=MAKS()
Esim. 2
Alla olevassa aineistossa on erään matematiikan opintojakson päättöarvosanojen jakauma.
| Arvosana | f |
|---|---|
| 10 | 2 |
| 9 | 4 |
| 8 | 6 |
| 7 | 8 |
| 6 | 7 |
| 5 | 3 |
| 4 | 1 |
Määritä GeoGebra-laskinohjelmistolla arvosanojen
a) mediaani
b) keskiarvo
c) (otos)keskihajonta.
Esim. 3
Alla olevassa aineistossa on taulukoituna opiskelijoiden eräällä matematiikan opintojaksolla saamat arvosanat.
| Arvosana |
|---|
| 7 |
| 8 |
| 8 |
| 8 |
| 7 |
| 7 |
| 7 |
| 5 |
| 9 |
| 6 |
| 4 |
| 5 |
| 7 |
| 7 |
| 8 |
| 8 |
| 8 |
| 7 |
| 7 |
| 7 |
| 6 |
| 9 |
| 8 |
| 9 |
| 6 |
| 7 |
Määritä Libre Office Calc -taulukkolaskentaohjelmalla arvosanojen
a) lukumäärä
b) mediaani
c) moodi
d) vaihteluväli
e) vaihteluvälin pituus
f) keskiarvo
g) keskihajonta.
1.4 Jatkuva tilastojakauma
Tilastollinen muuttuja on jatkuva, jos se voi saada minkä tahansa arvon tarkasteluvälillä. Esimerkiksi ihmisen pituus voi mittaustarkkuuden rajoissa saada minkä tahansa lukuarvon siltä lukuväliltä, jolla pituus voi vaihdella.
Jatkuvan tilastollisen muuttujan jakaumaa kutsutaan jatkuvaksi jakaumaksi.
Jatkuvia jakaumia on usein luontevinta käsitellä luokiteltuna.
Esim. 1
Eräällä MAB5-opintojaksolla selvitettiin ryhmän opiskelijoiden pituudet. Pituudet ovat taulukoituna alla olevassa aineistossa.
Opiskelijoiden pituudet (cm).
| 165 | 157 | 161 | 173 | 167 | 151 | 167 |
| 164 | 185 | 163 | 167 | 172 | 163 | 166 |
| 174 | 173 | 187 | 174 | 163 | 177 | 175 |
| 174 | 173 | 182 | 169 | 184 | 153 | 183 |
| 164 | 173 | 163 | 162 | 164 | 177 | 175 |
a) Luokittele pituudet neljään tasalevyiseen luokkaan taulukkolaskentaohjelmalla.
b) Määritä luokkien frekvenssit taulukkolaskentaohjelmalla.
c) Kokoa luokat ja frekvenssit luokitelluksi jatkuvaksi jakaumaksi.
d) Mikä on pituuksien moodiluokka?
- Kopioi aineisto taulukkoon.
- Selvitä aineiston pienin ja suurin arvo.
- Kirjoita taulukkoon luokat ja todelliset ylärajat.
- Määritä luokkien frekvenssit Taajuus-funktiolla.
Tilastolliset tunnusluvut luokitellulle aineistolla
Luokitellusta aineistoista keskiarvon ja keskihajonnan kaltaisten tunnuslukujen selvittämiseksi on tiedettävä luokkien luokkakeskukset, jotka ovat luokkien todellisten ala- ja ylärajojen keskiarvoja. Todelliset ala- ja ylärajat määritetään edellisen ja seuraavan luokan ylä- ja alarajan puoliväliin (poikkeuksena ikä).
Esim. 2
Määritä arvio esimerkin 1 pituuksien keskiarvolle ja keskihajonnalle luokitellusta aineistosta laskinohjelmalla (GeoGebra). Mikä on pituuksien moodiluokka?
- Määritä taulukkolaskentaohjelmassa luokkien todelliset ala- ja ylärajat ja luokkakeskukset niiden keskiarvona.
- Kopioi luokkakeskukset ja frekvenssit GeoGebraan.
- Valitse Yhden muuttujan analyysi ja Näytä tilastot.
Histogrammi
Histogrammi on pylväskuvaaja, jossa pylväät on ovat kiinni toisissaan. Jatkuvaa jakaumaa kuvataan yleensä histogrammilla.
Esim. 3
a) Määritä esimerkin 1 luokitteluille pituuksille suhteelliset frekvenssit taulukkolaskentaohjelmalla.
b) Piirrä taulukkolaskentaohjelmalla suhteellista jakaumaa kuvaava histogrammi.
Huom.
Histogrammi piirretään Libre Office Calc -taulukkolaskentaohjelmalla lisäämällä jatkuvalle jakaumalle pylväskaavio ohjattua kaavionluontitoimintoa käyttäen. Kun kaavio on luotu, klikataan vielä hiiren oikealla painikkeella kuvaajan pylvästä ja valitaan Muotoile arvosarja. Asetukset-välilehdeltä muutetaan Objektivälin (Spacing) arvoksi 0 %.
Kertymä
Kun frekvenssejä lasketaan yhteen saadaan summafrekvenssi, sf. Summafrekvenssi kuvaa, kuinka paljon havaintoja on kertynyt suuruusjärjestyksessä tiettyyn tilastomuuttujan arvoon mennessä.
Suhteellisille frekvensseille voidaan laska suhteellinen summafrekvenssi, sf %. Suhteellinen summafrekvenssi kuvaa, kuinka suuri osuus havainnoista on kertynyt tiettyyn tilastomuuttujan arvoon mennessä.
Luokitellun aineiston mediaaniluokka löydetään etsimällä se luokka, jonka kohdalla suhteellinen summafrekvenssi ylittää 50 prosentin rajan.
Havaintojen kertymää voidaan kuvata kertymäkuvaajalla.
Esim. 4
a) Määritä esimerkin 3 suhteelliselle jakaumalle suhteelliset summafrekvenssit.
b) Mikä on jakauman mediaaniluokka?
c) Piirrä opiskelijoiden pituuksien kertymäkuvaaja.
d) Kuinka pitkiä ovat alimpaan kvartiiliin kuuluvat opiskelijat eli mitä pituutta lyhyempiä on 25 % opiskelijoista?
- Kertymäkuvaaja määritetään luokkien todellisista ylärajoista ja suhteellisista summafrekvensseistä. Suhteellisen summafrekvenssin ensimmäisen arvon tulee olla 0 %.
- Lisää kaavio. Valitse kaaviotyypiksi XY (hajonta) ja Pisteet ja viivat.
- Valitse Näytä ruudukot -kohdasta X-akseli ja Y-akseli.
- Muotoile y-akselin asteikka välille 0 - 100 (%).
2 BINOMIJAKAUMA
2.1 Todennäköisyyden laskusääntöjä
Tapahtumat ovat riippumattomia, jos ne eivät vaikuta toisiinsa.
Riippumattomien tapahtumien kertolaskusääntö ( ja-sääntö)
Todennäköisyys riippumattomien tapahtumien tapahtumiselle yhdessä saadaan kertomalla tapahtumien todennäköisyydet keskenään.
Esim. 1
Matkalla asemalta torille on kahdet liikennevalot. Ensimmäiset ovat vihreänä 30 % ja toiset 40 % ajasta.
Millä todennäköisyydellä molemmat valot ovat vihreänä?
\( \begin{align} &P(\text{''molemmat vihreänä''})\\ &=P(\text{''1. vihreä'' ja ''2. vihreä''})\\ &=P(\text{''1. vihreä''})\cdot P(\text{''2. vihreä''})\\ &=0{,}3\cdot0{,}4\\ &=0{,}12 \end{align} \)
Vastaus: 12 %
Tapahtumat ovat erillisiä eli toisensa poissulkevia, jos niillä ei ole yhteisiä alkeistapauksia. Kaksi tapahtumaa ovat erillisiä, jos toisen tapahtuessa toinen ei voi tapahtua.
Erillisten tapahtumien yhteenlaskusääntö (tai-sääntö)
Todennäköisyys erillisistä tapahtumista vähintään yhden tapahtumiselle saadaan laskemalla tapahtumien todennäköisyydet yhteen.
Esim. 2
Millä todennäköisyydellä esimerkin 1 liikennevaloista vain yksi on vihreänä?
\(P(\text{''1. vihreä''})=0{,}3\quad\quad P(\text{''1. punainen''})=0{,}7\)
\(P(\text{''2. vihreä''})=0{,}4\quad\quad P(\text{''2. punainen''})=0{,}6\)
\( \begin{align} &P(\text{''vain yksi on vihreänä''})\\ &=P(\text{''1. vihreä'' ja ''2. punainen'' TAI ''1. punainen'' ja ''2. vihreä''})\\ &=0{,}3\cdot0{,}6+0{,}7\cdot0{,}4\\ &=0{,}18+0{,}28\\ &=0{,}46 \end{align} \)
Vastaus: 46 %
Tapahtuman ''tapahtuu \(A\)'' vastatapahtuma eli komplementtitapahtuma on ''ei tapahdu \(A\)''.
Tapahtuman \(A\) vastatapahtumaa merkitään \(\bar{A}\).
Vastatapahtuman todennäköisyys
Tapahtuma ja sen vastatapahtuma ovat erilliset ja sisältävät yhdessä kaikki perusjoukon alkeistapaukset. Siten tapahtuman todennäköisyyden ja vastatapahtuman todennäköisyyden summa on yksi eli varma tapahtuma: $$P(A) + P(\bar{A})=1.$$ Näin ollen tapahtuman todennäköisyys voidaan ilmoittaa vastatapahtuman avulla: $$P(A)=1-P(\bar{A}).$$
Esim. 3
Millä todennäköisyydellä kolmella peräkkäisellä nopan heitolla tulee ainakin yksi kuutonen?
Tapahtuma ''tulee ainakin yksi kuutonen'' on varsin monimutkainen. On helpompaa laskea todennäköisyys vastatapahtumaa ''ei tule yhtään kuutosta'' hyödyntäen.
\( \begin{align} &P(\text{''tulee ainakin yksi kuutonen''})\\ &=1-P(\text{''ei tule yhtään kuutosta''})\\ &=1-\frac{5}{6}\cdot\frac{5}{6}\cdot\frac{5}{6}\\ &=1-\left(\frac{5}{6}\right)^{3}\\ &=0{,}421296\ldots\\ &\approx 0{,}421 \end{align} \)
Vastaus: 0,421
Esim. 4
Oletetaan, että seuraavan päivän sää riippuu edellisen päivän säästä seuraavasti: Jos tänään on pouta, huomenna sataa 10 % todennäköisyydellä, ja jos tänään sataa, huomenna sataa 40 % todennäköisyydellä.
Millä todennäköisyydellä keskiviikkona sataa, jos maanantaina satoi?
Merkitään \(s\) = huomenna sataa ja \(p\) = huomenna ei sada (pouta).
Laaditaan puukaavio. Kaaviosta nähdään, että suotuisat vaihtoehdot todennäköisyydelle, että keskiviikkona sataa, kun maanantai satoi, ovat \(ss\) tai \(ps\).
\( \begin{align} &P(''\text{ke sataa, kun ma satoi}'')\\ &=P(ss)+P(ps)\\ &=0{,}4\cdot0{,}4+0{,}6\cdot0{,}1\\ &=0{,}16+0{,}06\\ &=0{,}22\\ &=22\ \%\\ \end{align} \)
Vastaus: 22 %
2.2 Toistokoe
Kertausta
Kuinka monella eri tavalla kolme valkoista ja yksi musta pallo voidaan asettaa jonoon, kun samanväristen pallojen eri järjestyksiä ei huomioida?
TAPA 1
\(\displaystyle{\binom{4}{3}=4}\)
Merkintä \(\binom{n}{k}\) luetaan ''\(n\) yli \(k\):n'' ja se näppäillään esimerkiksi SpeedCrunch-laskimeen ncr(n;k).
TAPA 2
\(\displaystyle{\frac{4!}{3!(4-3)!}=4}\)
Vastaus: 4 eri tavalla.
Toistokoe tarkoittaa, että
- satunnaisilmiötä toistetaan \(n\) kertaa
- kiinnostuksen kohteena on tapahtuman \(A\) esiintyminen \(k\) kertaa
- tapahtuman \(A\) todennäköisyys on vakio \(p\).
Esim. 1
Millä todennäköisyydellä nopanheitossa neljästä heitosta tasan kolme on kuutosia.
Satunnaisilmiö on nopanheitto. Satunnaisilmiötä toistetaan eli noppaa heitetään \(n=4\) kertaa. Tapahtuma \(A\) on ''tulee kuutonen'', ja kiinnostuksen kohteena on, tapahtuman \(A\) esiintyminen tasan \(k=3\) kertaa. Tapahtuman \(A\) todennäköisyys on \(p=\frac{1}{6}\) jokaisella heitolla.
Mahdolliset heittosarjat ovat: \(AAA\bar{A}\), \(AA\bar{A}A\), \(A\bar{A}AA\), \(\bar{A}AAA\).
Tapahtuma \(A\) voi sijoittua sarjoihin
\(\displaystyle{\binom{4}{3}=4}\)
eri tavalla.
Jokaisen sarjan todennäköisyys on sama eli kolmesti tapahtuman \(A\) todennäköisyys ja kerran vastatapahtuman \(\bar{A}\) todennäköisyys eli
\(\displaystyle{\left(\frac{1}{6}\right)^{3}\left(1-\frac{1}{6}\right)^{4-3}}.\)
Yhdistettynä todennäköisyys tasan kolmelle kuutoselle neljällä nopanheitolla on
\(\displaystyle{\binom{4}{3}\left(\frac{1}{6}\right)^{3}\left(1-\frac{1}{6}\right)^{4-3}}\)
\(\displaystyle{=\frac{20}{1296}^{(4}=\frac{5}{324}}\)
\(=0{,}015432\approx0{,}0154.\)
Vastaus: \(\frac{5}{324}\approx0{,}0154\).
Toistokokeen todennäköisyys
Olkoon tapahtuman \(A\) todennäköisyys \(p\). Tällöin
\(P(''A\ \text{tapahtuu}\ n\ \text{toistossa tasan}\ k\ \text{kertaa}'')\)
\(\displaystyle{=\binom{n}{k}p^{k}(1-p)^{n-k}}.\)
Esim. 2
Koripalloilija heittää vapaaheitolla korin \(80\ \%\) todennäköisyydellä. Oletetaan, että seuraavan heiton onnistumisen todennäköisyys on riippumaton edellisestä heitosta. Millä todennäköisyydellä koripalloilija heittää korin kahdeksalla peräkkäisellä vapaaheitolla
a) tasan kaksi kertaa
b) korkeintaan kaksi kertaa
c) vähintään kolme kertaa?
a) \(n=8, k=2, p=0{,}8\)
\(P(\)heittää korin tasan 2 kertaa\()\)
\(\displaystyle{=\binom{8}{2}0{,}8^{2}(1-0{,}8)^{8-2}}\)
\(=0{,}00114688\)
\(\approx0{,}00115\)
Vastaus: \(0{,}00115\)
b) \(n=8, k_1=0, k_2=1, k_3=2, p=0{,}8\)
\(P(\)heittää korin korkeintaan 2 kertaa\()\)
\(=P(\)ei heitä yhtään koria tai heittää korin tasan kerran tai heittää korin tasan 2 kertaa\()\)
\(\displaystyle{=\binom{8}{0}0{,}8^{0}(1-0{,}8)^{8-0}+\binom{8}{1}0{,}8^{1}(1-0{,}8)^{8-1}+\binom{8}{2}0{,}8^{2}(1-0{,}8)^{8-2}}\)
\(=0{,}00123136\)
\(\approx0{,}00123\)
Vastaus: \(0{,}00123\)
c) Tapahtuman ''heittää korin vähintään kolme kertaa'' vastatapahtuma on ''heittää korin korkeintaan kaksi kertaa'', eli b-kohdan perusteella:
\(P(\)heittää korin vähintään 3 kertaa\()\)
\(=1-P(\)heittää korin korkeintaan 2 kertaa\()\)
\(=1-0{,}00123136\)
\(=0{,}99876864\)
\(\approx0{,}999\)
Vastaus: \(0{,}999\)
2.3 Binomijakauma
Satunnaismuuttuja on funktio, joka liittää satunnaisilmiön jokaiseen alkeistapaukseen täsmälleen yhden reaaliluvun, jota kutsutaan satunnaismuuttujan arvoksi.
Jos satunnaismuuttujan arvot ovat erillisiä (esim. kokonaislukuja), kyseessä on diskreetti satunnaismuuttuja.
Satunnaismuuttujan todennäköisyysjakauma saadaan laskemalla satunnaismuuttujan jokaisen arvon todennäköisyys. Todennäköisyysjakauma voidaan diskreetin tilastollisen jakauman tavoin esittää taulukkona tai pylväskuvaajana.
Esim. 1
Heitetään kolikkoa neljä kertaa. Määritetään todennäköisyydet, että kruunia tulee tasan 0, 1, 2, 3 tai 4.
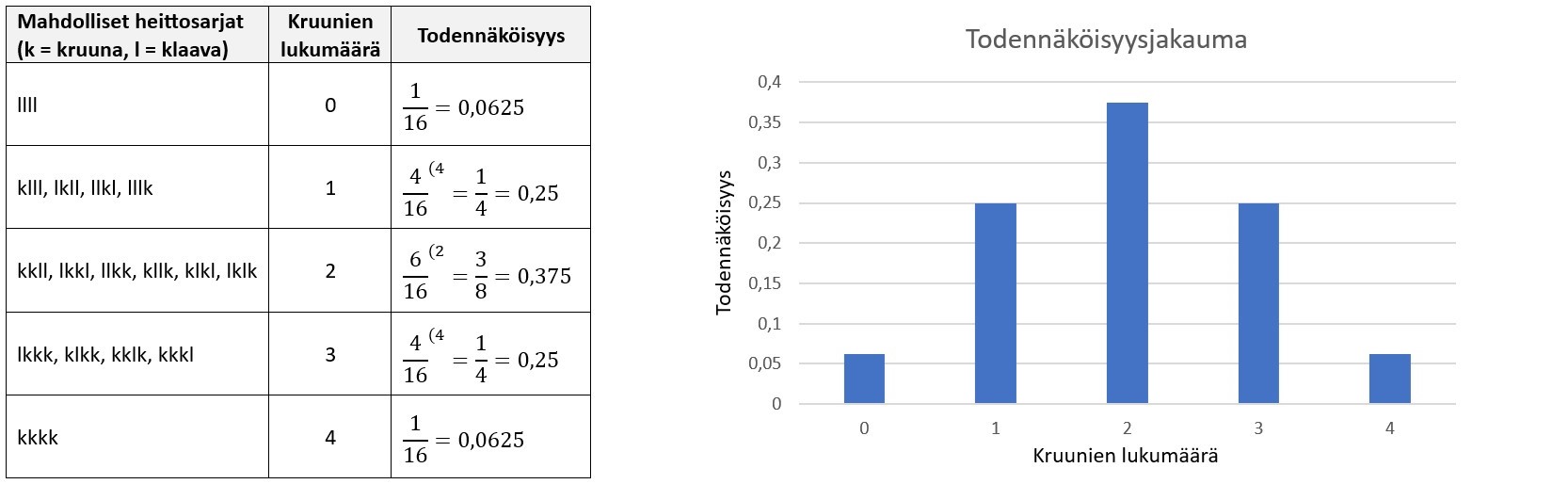
Vasemmanpuoleisessa taulukossa sarakkeessa Mahdolliset heittosarjat on lueteltu satunnaisilmiön Heitetään kolikkoa neljä kertaa kaikki alkeistapaukset. Satunnaismuuttuja on Kruunien lukumäärä, ja sen alla on satunnaismuuttujan saamat arvot. Sarakkeet Kruunien lukumäärä ja Todennäköisyys muodostavat todennäköisyysjakauman. Oikealla todennäköisyysjakauma esitettynä pylväskuvaajana.
Binomijakauma on diskreetti todennäköisyysjakauma, jonka satunnaismuuttujan arvoiksi voidaan valita tapahtuman \(A\) toteutumiskertojen \(k\) lukumäärä \(n\)-toistossa ja satunnaismuuttujan arvojen todennäköisyydet (eli pistetodennäköisyydet) voidaan laskea toistokokeen todennäköisyyksinä.
Merkintä
$$X\ \sim\ \text{Bin}(n,p)$$ tarkoittaa, että satunnaismuuttuja \(X\) noudattaa binomijakaumaa parametrein \(n\) (toistojen määrä) ja \(p\) (tapahtuman \(A\) todennäköisyys).
Binomijakauman pistetodennäköisyyden laskeminen
Olkoon satunnaismuuttuja$$X\ \sim\ \text{Bin}(n,p).$$ Tällöin satunnaismuuttujan \(X\) arvojen todennäköisyydet eli pistetodennäköisyydet lasketaan kaavalla $$P(X=k)=\binom{n}{k}p^{k}(p-1)^{n-k},$$ jossa tapahtuman \(A\) toteutumiskertojen määrä on \(k=0,1,2,\ \ldots\ ,n\).
Huom.
GeoGebran todennäköisyyslaskurilla voidaan määrittää binomijakauma ja todennäköisyyksiä \(P(k_{i_1}\leq X\leq k_{i_2})\). Valitse vaihtoehto Binomijakauma ja syötä arvot parametreille \(n\) ja \(p\).
Esim. 1
Noppaa heitetään 10 kertaa. Olkoon satunnaismuuttuja \(X\): "kuutosten lukumäärä". Määritä GeoGebran todennäköisyyslaskurilla satunnaismuuttujan jakauma. Millä todennäköisyydellä saadaan täsmälleen kolme kuutosta? Anna vastauksesi neljän desimaalin tarkkuudella.
Esim. 2
Olkoon \(X\sim \text{Bin}(10;0{,}2)\) ja \(Y\sim \text{Bin}(10;0{,}8)\). Havainnollista satunnaismuuttujien \(X\) ja \(Y\) jakaumia pylväskuvaajilla. Miten jakaumat eroavat toisistaan?
2.4 Todennäköisyyksiä binomijakaumalla
Esim. 1
Yo, lyhyt matematiikka, syksy 2025, t. 6 (A-osa)
HÄTÄPUHELUT (12 p.)
Hätäkeskukseen soitettiin vuonna 2022 yhteensä 2 920 000 puhelua. Niistä 694 600 oli vahinkopuheluita ja 37 600 häiriköintiä tai muuten asiattomia puheluita. Kutsutaan näitä turhiksi hätäpuheluiksi.
- Kuinka monta turhaa hätäpuhelua tuli keskimäärin yhden tunnin aikana? (3 p.)
- Arvioi binomijakauman kaavaa käyttämällä, millä todennäköisyydellä kymmenestä satunnaisesti valitusta puhelusta korkeintaan yksi oli turha. (9 p.)
Esim. 2
Tehtaassa on havaittu, että yksi kymmenestä valmistetusta tuotteesta on viallinen.
Arvioi binomijakauman avulla, millä todennäköisyydellä sadan tuotteen erästä
a) täsmälleen 10 on viallisia
b) korkeintaan 10 on viallisia
c) viallisia on yli 10 mutta alle 20.
Merkitään satunnaismuuttuja \(X\): ''viallisten lukumäärä''.
a) GeoGebran todennäköisyyslaskurilla:
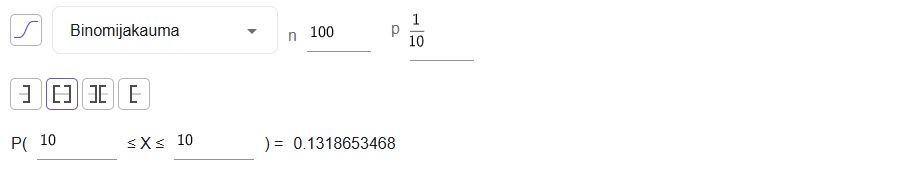
\(\begin{align} &P(\text{''täsmälleen 10 on viallista''})\\ \\ &=P(X=10)\\ \\ &\approx0{,}132. \end{align}\)
b) GeoGebran todennäköisyyslaskurilla:

\(\begin{align} &P(\text{''korkeintaa 10 viallista''})\\ \\ &=P(X\le10)\\ \\ &=P(0\le X\le10)\\ \\ &\approx0{,}583. \end{align}\)
c) GeoGebran todennäköisyyslaskurilla:
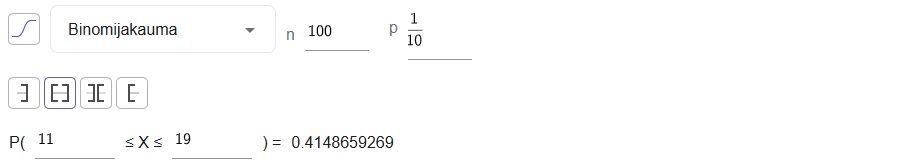
\(\begin{align} &P(\text{''viallisia on yli 10 mutta alle 20''})\\ \\ &=P(10\lt X\lt20)\\ \\ &=P(11\le X\le19)\\ \\ &\approx0{,}415. \end{align}\)
2.5 Odotusarvo ja keskihajonta
Satunnaismuuttujan todennäköisyysjakaumaa voidaan kuvata tunnusluvuilla kuten tilastollista jakaumaakin. Todennäköisyysjakauman tunnuslukuja ovat satunnaismuuttujan odotusarvo ja satunnaismuuttujan keskihajonta.
Binomijakauman odotusarvo ja keskihajonta
Olkoon satunnaismuuttuja$$X\ \sim\ \text{Bin}(n,p).$$ Tällöin satunnaismuuttujan odotusarvo on $$E(X)=\mu=np$$ ja keskihajonta $$D(X)=\sigma=\sqrt{np(1-p)}.$$
Satunnaismuuttujan odotusarvo ilmaisee, mitä lukua satunnaismuuttujan saamien arvojen keskiarvo lähestyy toistettaessa satunnaisilmiötä lukuisia kertoja.
Satunnaismuuttujan keskihajonta kuvaa satunnaismuuttujan arvojen vaihtelun suuruutta odotusarvon ympärillä.
Esim. 1
Satunnaismuuttuja noudattaa binomijakaumaa \(X\sim\text{Bin}(20;0{,}3)\). Laske satunnaismuuttujan
a) odotusarvo
b) keskihajonta.
\(n=20,\quad\quad p=0{,}3\)
a) Odotusarvo:
\(\begin{align} \mu&=np\\ \\ &=20\cdot0{,}3\\ \\ &=6{,}0 \end{align}\)
Vastaus: Odotusarvo on 6,0.
(Tulkinta: Pitkässä toistosarjassa satunnaismuuttujan arvojen keskiarvo lähestyy lukua 6,0.)
b) Keskihajonta:
\(\begin{align} \sigma&=\sqrt{np(1-p)}\\ \\ &=\sqrt{20\cdot0{,}3(1-0{,}3)}\\ \\ &=2{,}049\ldots\\ \\ &\approx2{,}0 \end{align}\)
Vastaus: Keskihajonta on noin 2,0.
(Tulkinta: Pitkässä toistosarjassa satunnaismuuttujan arvot sijoittuvat enimmäkseen välille noin 6,0-2,0=4,0 ja 6,0+2,0=8,0.)
Esim. 2
Tehtaassa on havaittu, että yksi kymmenestä valmistetusta tuotteesta on viallinen.
Tuotetta valmistetaan sadan kappaleen erä. Määritä viallisten tuotteiden
a) odotusarvo
b) keskihajonta.
\(n=100,\quad\quad p=0{,}1\)
a) Odotusarvo:
\(\begin{align} \mu&=np\\ \\ &=100\cdot0{,}1\\ \\ &=10{,}0 \end{align}\)
Vastaus: Odotusarvo on 10,0.
(Tulkinta: Kun tuotetta valmistetaan lukuisia eriä, viallisten tuotteiden määrän keskiarvo lähestyy lukua 10,0.)
b) Keskihajonta:
\(\begin{align} \sigma&=\sqrt{np(1-p)}\\ \\ &=\sqrt{100\cdot0{,}1(1-0{,}1)}\\ \\ &=3{,}0 \end{align}\)
Vastaus: Keskihajonta on 3,0.
(Tulkinta: Kun tuotetta valmistetaan lukuisia eriä, viallisten tuotteiden määrä vaihtelee enimmäkseen välillä 10,0-3,0=7,0 ja 10,0+3,0=13,0.)
3 NORMAALIJAKAUMA
3.1 Normaalijakauma
Normaalijakauma on jatkuva todennäköisyysjakauma. Todennäköisyysjakauma on jatkuva, jos satunnaismuuttuja voi saada minkä tahansa arvon tarkasteluvälillä. Monia luonnossa esiintyviä ilmiöitä voidaan mallintaa normaalijakaumalla.
Merkintä
$$X\ \sim\ \text{N}(\mu,\sigma)$$ tarkoittaa, että satunnaismuuttuja \(X\) noudattaa normaalijakaumaa parametrein \(\mu\) (odotusarvo) ja \(\sigma\) (keskihajonta).
Normaalijakauman tiheysfunktion kuvaaja on keskilinjan suhteen symmetrinen käyrä (ns. Gaussin käyrä tai ''kellokäyrä'').

Yllä olevan kuvan normaalijakauman odotusarvo on \(\mu=172\) ja keskihajonta \(\sigma=2\).
Normaalisti jakautuneella satunnaismuuttujalla todennäköisyys, että satunnaismuuttujan arvo on korkeintaan yhden keskihajonnan päässä odotusarvosta on 34 % + 34 % = 68 %, ja todennäköisyys, että satunnaismuuttujan arvo on yhden viiva kahden keskihajonnan päässä on 14 % + 14 % = 28 %. Todennäköisyys, että satunnaismuuttujan arvo on yli kahden keskihajonnan etäisyydellä odotusarvosta on 2 % + 2 % = 4 %.
Esim. 1
Oppitunnilla käydään kirjan kappaleen 8 esimerkki 1.
Esim. 2
Suomalaisten naisten keskipituus on 167,5 cm ja pituuden keskihajonta 5,40 cm. Suomalaisten miesten keskipituus on 181,0 cm ja pituuden keskihajonta 6,06 cm. Oletetaan suomalaisten miesten ja naisten pituudet normaalijakautuneiksi.
Millä todennäköisyydellä satunnaisesti valittu
a) nainen on alle 162 cm pitkä?
b) mies on yli 180 cm pitkä?
c) mies on pituudeltaan 175 - 185 cm?
3.2 Normaalijakaumatehtäviä
Esim. 1
Erään pääsykokeen keskiarvo oli 60 ja keskihajonta 12. Tulokset noudattivat normaalijaukaumaa. Mikä oli valintaan tarvittava pistemäärä, jos kokelaista 30 % valittiin?
Merkitään satunnaismuuttujaa \(X\): ''satunnaisesti poimittu opiskelija on tullut valituksi''.
Merkitään valintaan tarvittavaa pistemäärää \(x\).
Tehtävän tietojen perusteella tiedetään, että satunnaisesti poimittu opiskelija on tullut valituksi todennäköisyydellä \(30\ \%\) eli \(0{,}3\). Siis \(P(x\le X)=0{,}3\).
Ratkaistaan tehtävä GeoGebran todennäköisyyslaskurilla. Valitaan jakaumaksi Normaalijakauma. Syötetään odotusarvoksi 60 ja keskihajonnaksi 12. Valitaan vaihtoehto Oikeanpuoleinen, ja syötetään todennäköisyyden arvoksi \(0{,}3\). Luetaan vastaus satunnaismuuttujan arvon alarajasta.
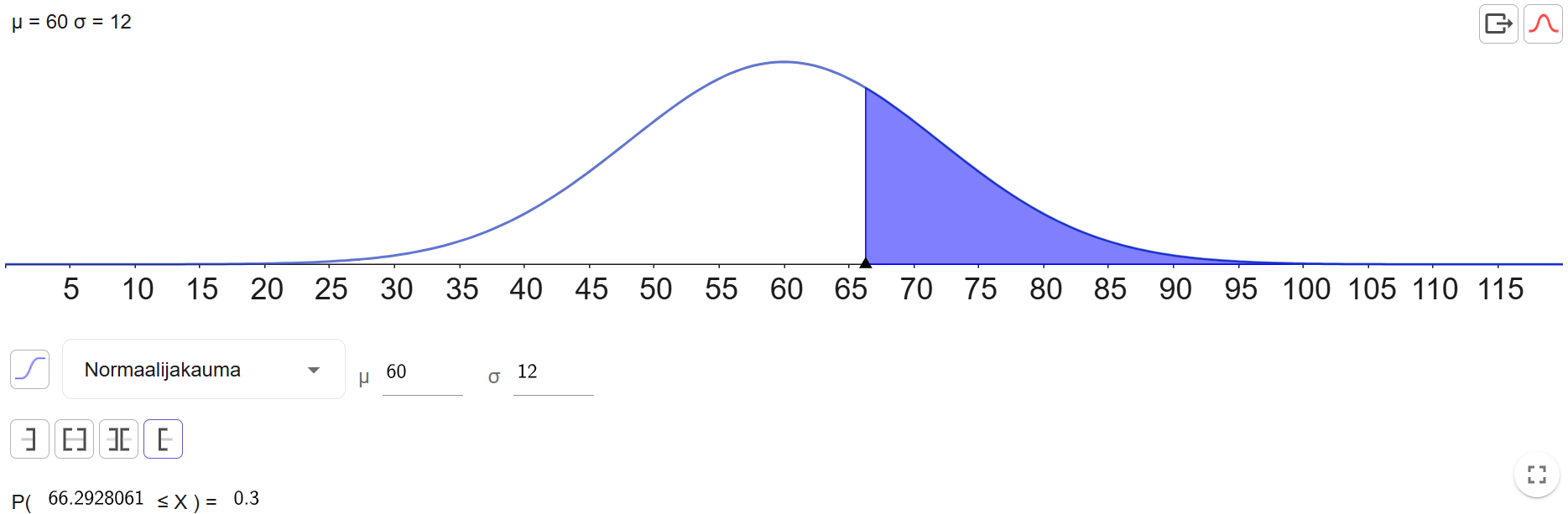
Vastaus: Valintaan tarvittava pistemäärä oli 66 pistettä.
Esim. 2
Suomalaisten naisten keskipituus on 167,5 cm ja pituuden keskihajonta 5,40 cm. Määritä keskiarvon suhteen symmetrinen väli, johon kuuluu 60 % naisista. Oletetaan suomalaisten naisten pituudet normaalijakautuneiksi.
Välillä tulee olla \(60\ \%\) naisista, joten välin ulkopuolelle jää \(100\ \%-60\ \%=40\ \%\) naisista. Symmetrian perusteella välin molemmin puolin jää \(\frac{40\ \%}{2}=20\ \%\) naisista.
Merkitään satunnaismuuttujaa \(X\): ''satunnaisesti poimitun naisen pituus''.
Ratkaistaan tehtävä GeoGebran todennäköisyyslaskurilla. Valitaan jakaumaksi Normaalijakauma. Syötetään odotusarvoksi 167,5 ja keskihajonnaksi 5,40. Alarajalla valitaan vaihtoehto Vasemmanpuoleinen ja ylärajalla Oikeanpuoleinen.
Määritetään välin alaraja \(a\):

\(P(X\le a)=0{,}2\quad\Leftrightarrow\quad a=162{,}955\ldots\approx163{,}0\).
Määritetään välin yläraja \(b\):

\(P(b\le X)=0{,}2\quad\Leftrightarrow\quad a=172{,}044\ldots\approx172{,}0\).
Vastaus: Väli on 163,0 cm - 172,0 cm.
Esim. 3
Yo, lyhyt matematiikka, syksy 2022, t. 9 (B1-osa)
SUOMALAISTEN MIESTEN JA NAISTEN PITUUDET (12 p.)
Suomalaisten naisten keskipituus on 167,5 cm ja pituuden keskihajonta 5,40 cm. Suomalaisten miesten keskipituus on 181,0 cm ja pituuden keskihajonta 6,06 cm. Oletetaan suomalaisten miesten ja naisten pituudet normaalijakautuneiksi.
- Laske todennäköisyys, että kun valitaan satunnaisesti yksi suomalainen mies ja yksi suomalainen nainen, niin molemmat ovat lyhyempiä kuin 160 cm. (6 p.)
- Annelin pituus on 171 cm. Hän laskee todennäköisyyden, että satunnaisesti valittu suomalainen nainen on häntä itseään pidempi mutta ei kuitenkaan enempää kuin x cm, ja saa tulokseksi 0,1. Mikä on Annelin käyttämä luku x? (6 p.)
Merkitään:
\(X\): ''satunnaisesti valitun naisen pituus''
\(Y\): ''satunnaisesti valitun miehen pituus''.
Naisten ja miesten pituudet ovat toisistaan riippumattomia.
\(\begin{align} &P(\text{''nainen on alle 160 cm ja mies on alle 160 cm''})\\ \\ &=P(X\le160)\cdot P(Y\le160) \quad \quad \mid (*)\\ \\ &=0{,}082433\ldots\ \cdot\ 0{,}00026477\ldots\\ \\ &=0{,}08269777\ldots\\ \\ &\approx0{,}0827\\ \\ \\ &(*)\ \text{GeoGebran todennäköisyyslaskurilla} \end{align}\)
Vastaus: \(0{,}0827\).Merkitään \(X\): ''satunnaisesti valitun naisen pituus''.
Tehtävässä annettujen tietojen perusteella todennäköisyys, että satunnaisesti valitun naisen pituus on välillä \(\left]171,171+x\right[\) on \(0{,}1\).
GeoGebran todennäköisyyslaskurilla saadaan \(P(X\le171)=0{,}74155\ldots\) .
Näin ollen \(P(X\le171+x)=0{,}74155\ldots+0{,}1=0{,}84155\ldots\) .
Selvitetään GeoGebran todennäköisyyslaskurilla \(a\), kun \(P(X\le a)=0{,}84155\ldots\) \(\Leftrightarrow a=172{,}904\ldots\) .
Siten \(x=a-171=172{,}904\ldots-171=1{,}904\ldots\approx1{,}9\).
Vastaus: \(x\approx1{,}9\).
3.3 Normitettu normaalijakauma
Normitetun normaalijakauman eli standardinormaalijakauman odotusarvo on \(0\) ja keskihajonta \(1\).
Merkintä
$$Z\ \sim\ \text{N}(0,1)$$ tarkoittaa, että satunnaismuuttuja \(Z\) noudattaa normitettua normaalijakaumaa parametrein \(0\) (odotusarvo) ja \(1\) (keskihajonta).
Huom.
Koska normitetun normaalijakauman odotusarvo on \(0\), niin sen tiheysfunktion kuvaaja on symmetrinen y-akselin suhteen.
Esim. 1
Satunnaismuuttuja \(Z\) noudattaa normitettua normaalijakaumaa. Määritä
a) todennäköisyys \(P(Z\le-1{,}2)\)
b) satunnaismuuttujan arvo \(a\), jolla \(P(Z\le a)=0{,}56\).
a) Määritetään todennäköisyys GeoGebran todennäköisyyslaskurilla. Valitaan jakaumaksi Normaalijakauma sekä parametrien arvoiksi \(\mu=0\) ja \(\sigma=1\). Valitaan lisäksi vaihtoehto Vasemmanpuoleinen, ja syötetään kenttään satunnaismuuttujien arvojen ylärajaksi \(-1{,}2\).
Tällöin \(P(Z\le-1{,}2)=0{,}115069\ldots\approx0{,}115\).
Vastaus: \(0{,}115\).
b) Tehdään määritykset GeoGebran todennäköisyyslaskuriin kuten a-kohdassa, mutta syötetään todennäköisyyden kenttään \(0{,}56\).
Tällöin \(P(Z\le 0{,}150969\ldots)=0{,}56\) eli \(a=0{,}150969\ldots\approx0{,}151.\)
Vastaus: \(0{,}151\).
Mikä tahansa normaalijakauma voidaan normittaa eli kuvata normitetulle normaalijakaumalle.
Normittaminen
Jos normaalijakaumassa satunnaismuuttuja \(X\sim \text{N}(\mu,\sigma)\), niin vastaavassa normitetussa normaalijakaumassa satunnaismuuttuja \(Z=\frac{X-\mu}{\sigma}\sim \text{N}(0,1)\).
Huom.
Satunnaismuuttujan \(X\) arvoa \(x\) vastaava normitettu arvo \(z=\frac{x-\mu}{\sigma}\) ilmaisee, kuinka monen keskihajonnan \(\sigma\) verran arvo \(x\) poikkeaa odotusarvosta \(\mu\) ja mihin suuntaan.
Esim. 2
Satunnaismuuttuja \(X\sim\text{N}(42,3)\). Laske arvoa \(x\) vastaava normitettu arvo. Kuinko monen keskihajonnan verran ja mihin suuntaan arvo \(x\) poikkeaa odotusarvosta 42?
a) \(x=48\)
b) \(x=30\)
Normaalijakaumaa noudattavan satunnaismuuttujan odotusarvo on \(\mu=42\) ja keskihajonta \(\sigma=3\).
a) Arvoa \(x=48\) vastaava normitettu arvo:
\(z=\frac{x-\mu}{\sigma}=\frac{48-42}{3}=\frac{6}{3}=2\).
Vastaus: Arvoa \(x=48\) vastaava normitettu arvo on \(2\).Arvo \(x=48\) poikkeaa odotusarvosta \(2\) keskihajonnan verran ylöspäin.
b) Arvoa \(x=30\) vastaava normitettu arvo:
\(z=\frac{x-\mu}{\sigma}=\frac{30-42}{3}=\frac{-12}{3}=-4\).
Vastaus: Arvoa \(x=30\) vastaava normitettu arvo on \(-4\). Arvo \(x=30\) poikkeaa odotusarvosta \(4\) keskihajonnan verran alaspäin.
Esim. 3
Kahvi myydään 500 g pakkauksissa. Automaattisesti pakatun kahvin määrä pakkauksessa noudattaa normaalijakaumaa. Mikä on odotusarvon oltava, jos keskihajonta on 4 g ja 90 prosentissa pakkauksista on oltava kahvia vähintään 500 g?
Merkitään \(X\sim\text{N}(\mu,4)\).
Normitettuna \(Z=\frac{X-\mu}{4}\sim\text{N}(0,1)\).
Arvoa \(x=500\) (g) vastaava normitettu arvo on \(z=\frac{500-\mu}{4}\).
Määritetään GeoGebran todennäköisyyslaskurilla todennäköisyyttä \(90\ \%=0{,}9\) vastaavan normitetun normaalijakauman arvon alaraja \(z\). Valitaan jakaumaksi Normaalijakauma sekä parametrien arvoiksi \(\mu=0\) ja \(\sigma=1\). Valitaan lisäksi vaihtoehto Oikeanpuoleinen, ja syötetään kenttään todennäköisyyden arvoksi \(0{,}9\).
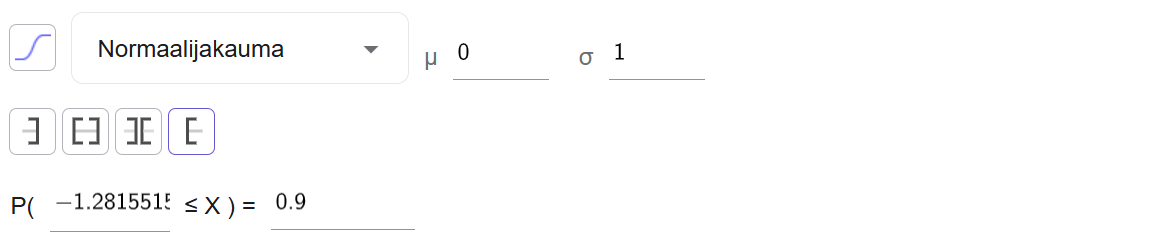
Tällöin \(P(z\le Z)=0{,}9\) eli \(z=-1{,}281551\ldots\approx-1{,}28\).
Ratkaistaan odotusarvo \(\mu\) yhtälöstä \(z=\frac{500-\mu}{4}\), kun \(z\approx-1{,}28\).
\(\begin{align} -1{,}28&=\frac{500-\mu}{4}\quad\mid\cdot\,4\\ \\ -5{,}12&=500-\mu\\ \\ \mu&=500+5{,}12\\ \\ &=505{,}12\\ \\ &\approx505 \end{align}\)
Vastaus: Odotusarvon on oltava 505 g.
3.4 Normaalijakauma ja binomijakauma
Toistokokeeseen liittyviä todennäköisyyksiä voidaan mallintaa binomijakauman avulla. Kun toistojen lukumäärä kasvaa, binomijakauman kuvaajan muoto lähestyy normaalijakauman kuvaajaa.
Esim. 1
Satunnaismuuttuja \(X\sim\text{Bin}(n;0{,}2)\). Vertaa GeoGebran todennäköisyyslaskurilla binomijakauman ja normaalijakauman muotoa, kun
a) \(n=5\)
b) \(n=50\)
c) \(n=150\).
Esimerkissä 1 GeoGebran työkalu sovittaa binomijakaumaan normaalijakauman, jolla on sama odotusarvo ja keskihajonta kuin binomijakaumalla.
Binomijakauman odotusarvo \(\mu\) ja keskihajonta \(\sigma\) voitiin laskea, jos tunnettiin toistokokeen toistojen lukumäärä \(n\) ja toistettavan tapahtuman todenköisyys \(p\).
Binomijakauman odotusarvo
\(\mu=np\).
Binomijakauman keskihajonta
\(\sigma=\sqrt{np(1-p)}\).
Esim. 2
Kolikkoa heitetään 20 kertaa. Määritä todennäköisyys, että saadaan täsmälleen 12 kruunaa
a) toistokokeen todennäköisyyden laskukaavalla
b) mallintamalla normaalijakaumalla.
a) \(n=20,\quad k=12,\quad p=0{,}5\)
\(P(\text{''saadaan täsmälleen 12 kruunaa''})\)
\(\displaystyle{=\binom{20}{12}0{,}5^{12}(1-0{,}5)^{20-12}}\quad\mid\text{CAS-laskin}\)
\(=0{,}120134\ldots\)
\(\approx0{,}120\)
Vastaus: \(0{,}120\).
b) Odotusarvo:
\(\begin{align} \mu&=np\\ \\ &=20\cdot0{,}5\\ \\ &=10 \end{align}\)
Keskihajonta:
\(\begin{align} \sigma&=\sqrt{np(1-p)}\\ \\ &=\sqrt{20\cdot0{,}5(1-0{,}5)}\\ \\ &=2{,}236067\ldots\\ \\ &\approx2{,}236 \end{align}\)
Määritetään todennäköisyys GeoGebran todennäköisyyslaskurilla käyttäen normaalijakaumaa odotusarvona \(\mu=10\) ja keskihajontana \(\sigma\approx2{,}236\).
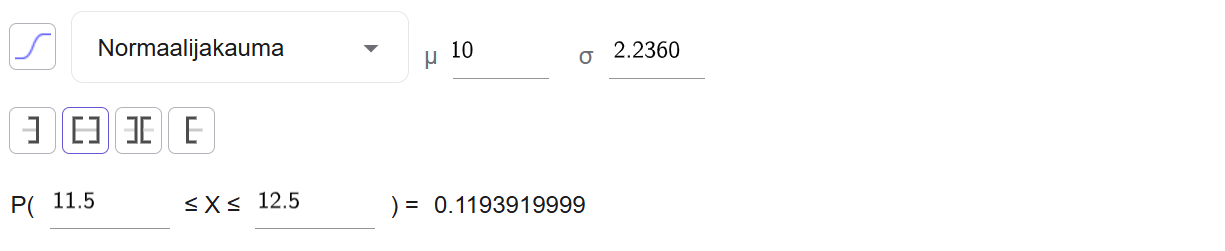
\(\begin{align} &P(\text{''saadaan täsmälleen 12 kruunaa''})\\ \\ &=P(11{,}5\le X\le12{,}5)\\ \\ &=0{,}119391\ldots\\ \\ &\approx0{,}119 \end{align}\)
Vastaus: \(0{,}119\).
Esim. 3
Jousiampuja ampuu kympin todennäköisyydellä 0,4. Oletetaan, että peräkkäisten ammuntojen tulokset ovat riippumattomia. Arvioi normaalijakaumalla todennäköisyyttä, että jousiampuja ampuu 500 peräkkäisellä kerralla 200 - 210 kymppiä.
Koska ammuntojen tulokset ovat riippumattomia, kyseessä on toistokoe:
\(n=500,\quad p=0{,}4\).
Satunnaismuuttuja ammunnan tulos \(X\sim\text{Bin}(500;0{,}4)\).
Arvioidaan binomijakaumaa normaalijakaumalla.
Odotusarvo:
\(\begin{align} \mu&=np\\ \\ &=500\cdot0{,}4\\ \\ &=200 \end{align}\)
Keskihajonta:
\(\begin{align} \sigma&=\sqrt{np(1-p)}\\ \\ &=\sqrt{500\cdot0{,}4(1-0{,}4)}\\ \\ &=10{,}954451\ldots\\ \\ &\approx10{,}954 \end{align}\)
Siispä likimain satunnaismuuttuja ammunnan tulos \(X\sim\text{N}(200;10{,}954)\).
Käytetään GeoGebran todennäköisyyslaskuria.

\(\begin{align} &P(\text{''saadaan 200 - 210 kymppiä''})\\ \\ &=P(199{,}5\le X\lt210{,}5)\\ \\ &=0{,}349311\ldots\\ \\ &\approx0{,}349 \end{align}\)
Vastaus: \(0{,}349\).
3.5 Normaalijakauman taulukko
Normitetun normaalijakauman kertymäfunktion taulukoitujen arvojen avulla voidaan ratkoa binomi- ja normaalijakaumien todennäköisyyksiin liittyviä ongelmia silloin, kun käytössä ei ole tähän soveltuvia ohjelmistoja.
Esim. 1
Määritä normaalijakauman taulukon avulla todennäköisyys \(P(-1{,}21\le Z\le0{,}96)\).
Todennäköisyyksiä voidaan tarkastella normaalijakauman kuvaajan alle jäävinä pinta-aloina.
\(\begin{align} &P(-1{,}21\le Z\le0{,}96)\\ \\ &=P(Z\le0{,}96)-P(Z\le-1{,}21)\\ \\ &=\Phi(0{,}96)-\Phi(-1{,}21)\\ \\ &=\Phi(0{,}96)-(1-\Phi(1{,}21))\\ \\ &=0{,}8315-(1-0{,}8869)\\ \\ &=0{,}8315-0{,}1131\\ \\ &=0{,}7184 \end{align}\)
Vastaus: \(0{,}7184\).
Esim. 2
Suomalaisten naisten keskipituus on 167,5 cm ja pituuden keskihajonta 5,40 cm. Oletetaan suomalaisten naisten pituudet normaalijakautuneiksi. Kuinka monta prosenttia naisista on alle 165 cm pitkiä?
On laskettava todennäköisyys, että satunnaisesti valittu nainen on alle 165 cm. Merkitään satunnaismuuttuja \(X\): ''satunnaisesti valitun naisen pituus''.
\(\begin{align} &P(X\lt165)\quad\quad\mid\text{Normitetaan.}\\ \\ &=P\left(Z\lt\frac{165-167{,}5}{5{,}40}\right)\\ \\ &=P(Z\lt-0{,}4629\ldots)\\ \\ &\approx P(Z\lt-0{,}46)\\ \\ &=\Phi(-0{,}46)\\ \\ &=1-\Phi(0{,}46)\\ \\ &=1-0{,}6772\\ \\ &=0{,}3228\\ \\ &\approx0{,}32\\ \\ &=32\ \% \end{align}\)
Vastaus: \(32\ \%\).
Esim. 3
Suomalaisten naisten keskipituus on 167,5 cm ja pituuden keskihajonta 5,40 cm. Oletetaan suomalaisten naisten pituudet normaalijakautuneiksi. Määritä pituus, jota lyhyempiä on 90 % suomalaisista naisista.
Merkitään satunnaismuuttuja \(X\): ''satunnaisesti valitun naisen pituus''. Merkitään kysyttyä pituuden arvoa \(x\).
Normittaminen:
\(z=\dfrac{x-167{,}5}{5{,}40}\).
Määritetään luku \(z\) normaalijakauman taulukon avulla:
\(\begin{align} P(Z\lt z)&=0{,}90\\ \\ z&=1{,}2816 \end{align}\)
Ratkaistaan luku \(x\) normitusyhtälöstä:
\(\begin{align} z&=\frac{x-167{,}5}{5{,}40}\quad\mid z=1{,}2816\\ \\ 1{,}2816&=\frac{x-167{,}5}{5{,}40}\quad\mid \cdot\,5{,}40\\ \\ 5{,}40\cdot1{,}2816&=x-167{,}5\\ \\ 5{,}40\cdot1{,}2816+167{,}5&=x\\ \\ x&=174{,}42064\approx174 \end{align}\)
Vastaus: Pituus on \(174\ \text{cm}\).
4 LUOTTAMUSVÄLI
4.1 Keskiarvon keskivirhe
Keskiarvon keskivirhe kuvaa, kuinka paljon otoskeskiarvot poikkeavat keskimäärin perusjoukon keskiarvosta.
Keskiarvon keskivirhe
\(s_{\bar{x}}=\dfrac{s}{\sqrt{n}}\),
missä \(s\) on perusjoukon keskihajonta ja \(n\) on otoskoko.
Huom.
Jos otoskoko \(n\) on vähintään 30, voidaan perusjoukon keskihajonnan sijasta käyttää otoskeskihajontaa.
Otoskeskiarvojen arvioiminen normaalijakaumalla
Perusjoukosta poimittujen kaikkien mahdollisten yhtä suurten otosten otoskeskiarvot noudattavat normaalijakaumaa, jonka
- odotusarvo on perusjoukon keskiarvo ja
- keskihajonta keskiarvon keskivirhe.
Esim. 1
Oppikirjan kpl 13 E1.
4.2 Otoskeskiarvon luottamusväli
Virhemarginaali ilmaisee, kuinka paljon perusjoukon keskiarvo enintään poikkeaa otoskeskiarvosta.
Keskiarvon luottamusväli on lukuväli, jolla perusjoukon keskiarvo on tietyllä todennäköisyydellä.
Luottamusvälin pituus määräytyy sen mukaan, kuinka suurella varmuudella eli luottamustasolla virhemarginaali halutaan tietää. Jos esimerkiksi käytetään 95 %:n luottamustasoa, niin luottamusväli sisältää 95 %:n varmuudella perusjoukon todellisen keskiarvon.
Luottamustasoja vastaavia kriittisiä arvoja on taulukoitu.
| Luottamustaso | Kriittinen arvo |
|---|---|
| 95 % | 1,96 |
| 99 % | 2,58 |
| 99,9 % | 3,29 |
Keskiarvon virhemarginaali
Keskiarvon virhemarginaali lasketaan:
\(\text{kriittinen arvo}\cdot\frac{s}{\sqrt{n}}\),
missä \(s\) on perusjoukon keskihajonta ja \(n\) on otoskoko.
Keskiarvon luottamusväli
\(\left[\bar{x}-\text{virhemarginaali},\bar{x}+\text{virhemarginaali}\right]\),
missä \(\bar{x}\) on otoskeskiarvo.
Huom.
Jos otoskoko \(n\) on vähintään 30, voidaan perusjoukon keskihajonnan sijasta käyttää jälleen otoskeskihajontaa.
Esim. 1
Oppikirjan kpl 13 E2.
4.3 Prosenttiosuuden luottamusväli
Prosenttiosuuden luottamusväli eli suhteellisen osuuden luottamusväli on lukuväli, jolla prosenttiosuus on tietyllä todennäköisyydellä.
Prosenttiosuuden virhemarginaali
Prosenttiosuuden virhemarginaali lasketaan:
\(\text{kriittinen arvo}\cdot\sqrt{\frac{p(1-p)}{n}}\),
missä \(p\) on otoksesta määritetty prosenttiosuus desimaalilukuna ja \(n\) on otoskoko.
Prosenttiosuuden luottamusväli
\(\left[p-\text{virhemarginaali},p+\text{virhemarginaali}\right]\),
missä \(p\) on otoksesta määritetty prosenttiosuus desimaalilukuna.
Esim. 1
Oppikirjan kpl 14 E1.